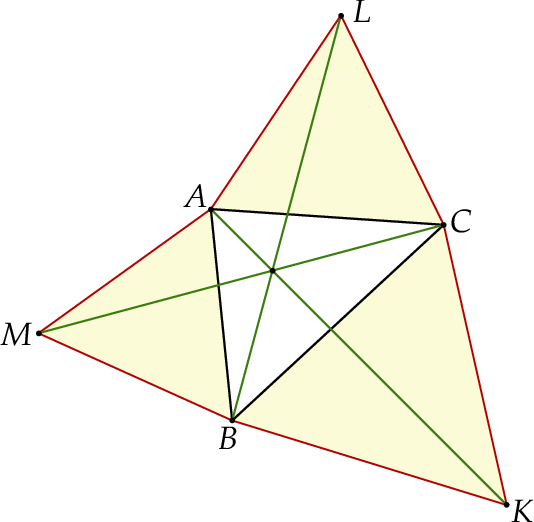
Każdy kąt trójkąta 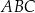 ma miarę mniejszą niż
ma miarę mniejszą niż 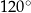 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 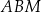 ,
, 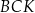 i
i 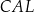 (zobacz rysunek).
(zobacz rysunek).
-
Wykaż, że
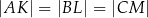 .
. -
Wykaż, że proste
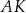 ,
, 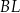 i
i 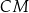 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Każdy kąt trójkąta 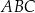 ma miarę mniejszą niż
ma miarę mniejszą niż 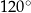 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 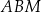 ,
, 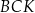 i
i 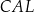 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że 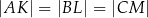 .
.
Wykaż, że proste 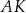 ,
, 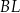 i
i 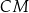 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
W trójkącie 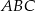 połączono środki boków i otrzymano trójkąt
połączono środki boków i otrzymano trójkąt 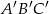 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 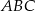 i
i 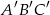 są podobne.
są podobne.
Punkty 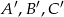 są środkami odpowiednio boków
są środkami odpowiednio boków 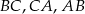 trójkąta
trójkąta 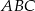 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 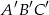 jest przystający do trójkąta
jest przystający do trójkąta 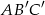 .
.
Trójkąt 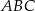 jest ostrokątny oraz
jest ostrokątny oraz 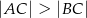 . Dwusieczna
. Dwusieczna 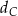 kąta
kąta 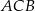 przecina bok
przecina bok 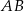 w punkcie
w punkcie 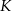 . Punkt
. Punkt 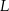 jest obrazem punktu
jest obrazem punktu 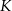 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 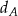 kąta
kąta 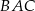 , punkt
, punkt 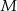 jest obrazem punktu
jest obrazem punktu 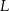 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 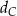 kąta
kąta 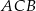 , a punkt
, a punkt 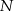 jest obrazem punktu
jest obrazem punktu 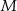 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 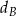 kąta
kąta 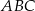 (zobacz rysunek).
(zobacz rysunek).
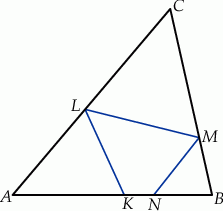
Udowodnij, że na czworokącie 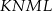 można opisać okrąg.
można opisać okrąg.
Na bokach 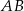 ,
, 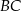 i
i 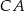 trójkąta
trójkąta 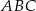 wybrano odpowiednio punkty
wybrano odpowiednio punkty 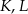 i
i 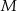 w ten sposób, że
w ten sposób, że 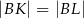 i
i 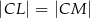 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 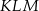 przecina bok
przecina bok 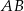 tego trójkąta w punkcie
tego trójkąta w punkcie 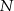 takim, że
takim, że 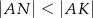 (zobacz rysunek).
(zobacz rysunek).
Udowodnij, że 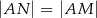 .
.
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
Odcinki 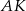 i
i 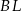 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 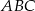 , a punkt
, a punkt 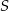 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
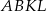 można opisać okrąg;
można opisać okrąg; 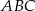 i
i 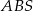 mają promienie równej długości.
mają promienie równej długości.Proste zawierające wysokości trójkąta ostrokątnego 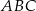 przecinają boki
przecinają boki 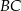 ,
, 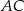 i
i 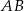 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 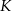 ,
, 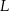 i
i 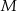 . Wykaż, że jeżeli trójkąt
. Wykaż, że jeżeli trójkąt 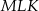 jest podobny do trójkąta
jest podobny do trójkąta 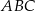 , to trójkąt
, to trójkąt 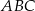 jest równoboczny.
jest równoboczny.
W trójkącie 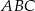 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 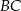 ,
, 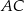 i
i 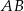 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 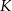 ,
, 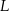 oraz
oraz 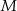 . Punkt
. Punkt 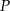 jest punktem przecięcia tych dwusiecznych. Na czworokątach
jest punktem przecięcia tych dwusiecznych. Na czworokątach 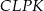 oraz
oraz 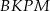 można opisać okrąg. Udowodnij, że trójkąt
można opisać okrąg. Udowodnij, że trójkąt 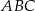 jest równoboczny.
jest równoboczny.
Trójkąty 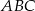 i
i 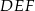 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
W trójkącie 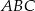 miara kąta
miara kąta 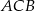 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 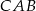 . Dwusieczna kąta
. Dwusieczna kąta 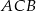 dzieli trójkąt
dzieli trójkąt 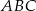 na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta
na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta 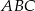 .
.
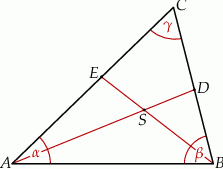
Miary kątów trójkąta 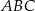 są równe
są równe 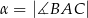 ,
, 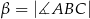 i
i 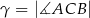 . Punkt
. Punkt 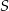 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 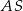 i
i 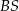 przecinają boki
przecinają boki 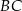 i
i 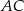 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 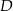 i
i 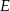 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że jeżeli 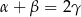 , to na czworokącie
, to na czworokącie  można opisać okrąg.
można opisać okrąg.
W trójkącie 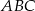 na boku
na boku 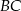 zaznaczono punkt
zaznaczono punkt 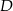 , na boku
, na boku 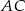 zaznaczono punkt
zaznaczono punkt 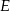 , na boku
, na boku 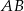 punkt
punkt 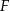 . Poprowadzono okręgi
. Poprowadzono okręgi 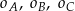 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 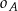 należą punkty
należą punkty 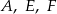 , do
, do 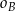 – punkty
– punkty 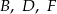 , a do
, a do 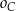 – punkty
– punkty 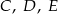 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Okrąg 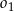 przechodzi przez wierzchołek
przechodzi przez wierzchołek 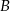 trójkąta
trójkąta 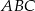 i przecina jego boki
i przecina jego boki 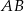 i
i 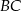 odpowiednio w punktach
odpowiednio w punktach 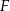 i
i 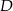 . Okrąg
. Okrąg 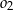 przechodzi przez wierzchołek
przechodzi przez wierzchołek 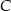 , przecina okrąg
, przecina okrąg 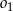 w punkcie
w punkcie 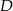 oraz w punkcie
oraz w punkcie 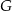 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 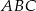 . Ponadto okrąg
. Ponadto okrąg 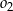 przecina bok
przecina bok 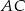 trójkąta w punkcie
trójkąta w punkcie 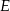 .
.
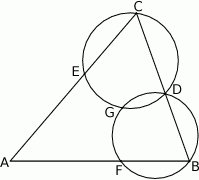
Udowodnij, że punkt 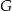 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 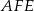 .
.
W trójkącie 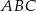 na boku
na boku 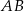 wybrano takie punkty
wybrano takie punkty 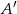 i
i 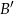 , że
, że
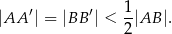
Przez punkty 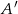 i
i 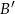 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 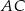 i
i 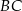 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 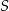 . Wykaż, że odcinek
. Wykaż, że odcinek 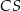 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 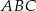 .
.
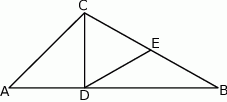
Dany jest trójkąt 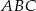 . Odcinek
. Odcinek 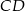 jest wysokością tego trójkąta, punkt
jest wysokością tego trójkąta, punkt 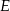 jest środkiem boku
jest środkiem boku 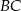 (tak jak na rysunku) i
(tak jak na rysunku) i 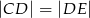 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 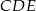 jest równoboczny.
jest równoboczny.
Wykaż, że jeżeli długości 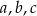 boków trójkąta spełniają równość
boków trójkąta spełniają równość
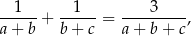
to promień okręgu opisanego na tym trójkącie jest równy 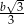 .
.
W trójkącie 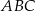 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 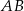 i
i 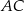 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 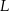 i
i 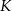 . Punkt
. Punkt 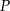 jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta
jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta 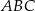 spełniają warunki:
spełniają warunki: 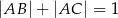 oraz
oraz
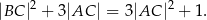
Udowodnij, że punkt 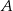 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 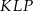 .
.
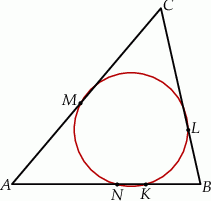
W trójkącie 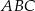 punkt
punkt 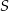 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 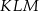 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 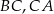 i
i 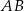 odpowiednio.
odpowiednio.
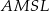 można opisać okrąg.
można opisać okrąg. 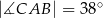 oraz
oraz 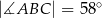 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 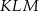 .
.Na bokach 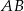 ,
, 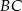 i
i 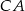 trójkąta
trójkąta 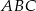 wybrano odpowiednio punkty
wybrano odpowiednio punkty 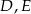 i
i 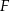 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 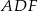 ,
, 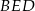 i
i 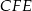 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
W trójkącie 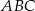 punkt
punkt 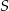 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 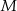 i
i 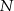 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 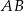 i
i 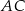 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 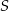 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 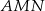 .
.
Na bokach 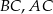 i
i 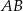 trójkąta
trójkąta 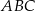 wybrano odpowiednio punkty
wybrano odpowiednio punkty 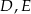 i
i 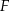 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 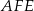 i
i 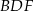 są styczne, to punkt
są styczne, to punkt 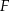 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 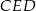 .
.
Odcinki 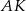 i
i 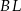 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 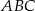 , a punkt
, a punkt 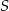 punktem ich przecięcia. Wykaż, że podobne są trójkąty:
punktem ich przecięcia. Wykaż, że podobne są trójkąty:
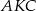 i
i 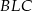 ;
; 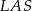 i
i 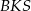 ;
; 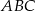 i
i 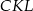 .
.