Niech  i
i 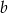 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 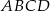 , zaś
, zaś 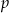 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 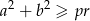 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok/Udowodnij
Czworokąt 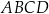 jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach
jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach 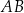 i
i 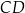 są styczne zewnętrznie, to równoległobok
są styczne zewnętrznie, to równoległobok 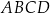 jest rombem.
jest rombem.
Prosta przechodząca przez wierzchołek 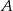 równoległoboku
równoległoboku 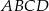 przecina jego przekątną
przecina jego przekątną 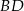 w punkcie
w punkcie 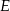 i bok
i bok 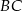 w punkcie
w punkcie 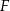 , a prostą
, a prostą 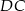 w punkcie
w punkcie 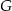 . Udowodnij, że
. Udowodnij, że
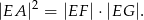
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Dany jest równoległobok 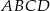 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 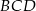 jest styczny do przekątnej
jest styczny do przekątnej 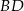 w punkcie
w punkcie 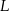 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 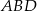 ma środek
ma środek 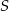 i jest styczny do boku
i jest styczny do boku 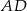 w punkcie
w punkcie 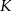 .
.
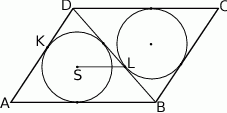
Wykaż, że jeżeli odcinek 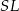 jest równoległy do prostej
jest równoległy do prostej 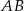 , to
, to 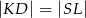 .
.
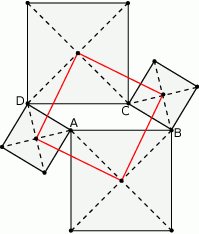
Wykazać, że odcinki łączące kolejne środki kwadratów zbudowanych na bokach równoległoboku tworzą także kwadrat.
W równoległoboku 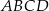 punkt
punkt 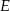 jest takim punktem boku
jest takim punktem boku 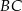 , że
, że 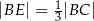 . Z wierzchołka
. Z wierzchołka 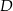 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 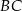 w punkcie
w punkcie 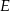 . Proste
. Proste 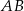 i
i 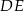 przecinają się w punkcie
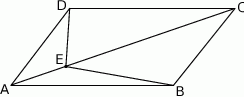
przecinają się w punkcie 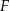 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 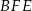 stanowi
stanowi 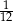 pola równoległoboku
pola równoległoboku 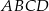 .
.
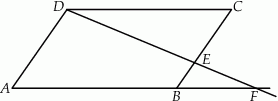
Punkt 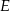 jest środkiem boku
jest środkiem boku 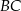 równoległoboku
równoległoboku 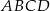 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 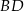 w punkcie
w punkcie 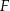 . Wykaż, że
. Wykaż, że 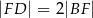 .
.
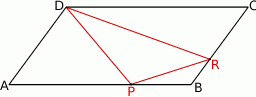
W równoległoboku 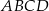 punkt
punkt 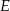 jest środkiem boku
jest środkiem boku 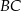 . Z wierzchołka
. Z wierzchołka 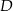 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 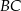 w punkcie
w punkcie 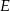 . Proste
. Proste 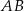 i
i 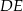 przecinają się w punkcie
przecinają się w punkcie 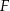 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 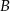 jest środkiem odcinka
jest środkiem odcinka 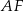 .
.
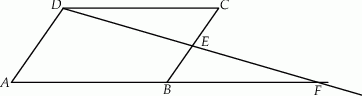
W równoległoboku wpisano dwa przystające okręgi styczne zewnętrznie do siebie (patrz rysunek). Wykaż, że średnica każdego z tych okręgów jest równa różnicy długości dłuższego i krótszego boku tego równoległoboku.
Na rysunku przedstawiono równoległobok 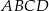 i trójkąt
i trójkąt 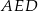 . Punkt
. Punkt 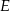 leży na odcinku
leży na odcinku 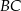 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 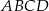 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 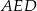 .
.
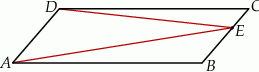
Kąt ostry równoległoboku ma miarę 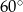 . Stosunek kwadratów długości przekątnych jest równy
. Stosunek kwadratów długości przekątnych jest równy 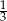 . Wykaż, że ten równoległobok jest rombem.
. Wykaż, że ten równoległobok jest rombem.
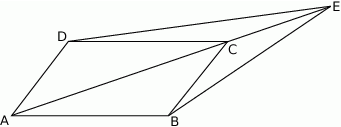
Dany jest równoległobok 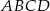 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 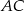 wybrano punkt
wybrano punkt 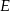 tak, że
tak, że 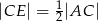 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 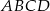 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 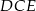 .
.
Na przekątnej 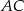 równoległoboku
równoległoboku 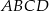 wybrano punkt
wybrano punkt 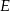 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 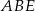 i
i 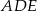 mają równe pola.
mają równe pola.
Punkty 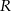 i
i 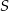 są środkami boków odpowiednio
są środkami boków odpowiednio 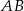 i
i 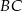 równoległoboku
równoległoboku 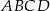 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 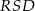 jest równe
jest równe pola tego równoległoboku.
pola tego równoległoboku.
W równoległoboku 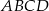 punkt
punkt 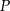 jest takim punktem boku
jest takim punktem boku 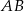 , że
, że 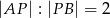 . Punkt
. Punkt 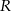 jest takim punktem boku
jest takim punktem boku 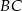 , że
, że 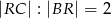 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 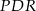 jest 5 razy większe od pola trójkąta
jest 5 razy większe od pola trójkąta 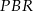 .
.
Na bokach 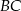 i
i 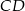 równoległoboku
równoległoboku 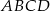 zbudowano kwadraty
zbudowano kwadraty 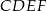 i
i 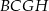 (zobacz rysunek).
(zobacz rysunek).
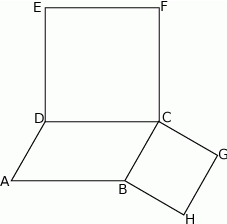
Udowodnij, że 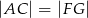 .
.
W równoległoboku 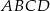 , w którym
, w którym 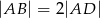 punkt
punkt 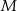 jest środkiem boku
jest środkiem boku 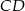 . Wykaż, że trójkąt
. Wykaż, że trójkąt 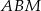 jest prostokątny.
jest prostokątny.
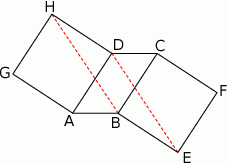
Na przeciwległych bokach równoległoboku 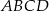 zbudowano kwadraty
zbudowano kwadraty 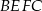 i
i 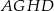 . Udowodnij, że proste
. Udowodnij, że proste 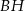 i
i 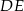 są równoległe.
są równoległe.
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Uzasadnij, że dwusieczne kątów 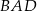 i
i 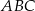 równoległoboku
równoległoboku 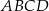 są prostopadłe.
są prostopadłe.
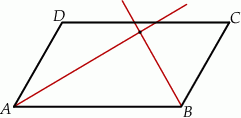
Na przekątnej 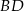 równoległoboku
równoległoboku 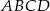 obrano dowolny punkt
obrano dowolny punkt 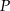 . Wykaż, że pola trójkątów
. Wykaż, że pola trójkątów 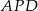 i
i 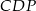 są równe.
są równe.
Na przekątnej 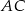 równoległoboku
równoległoboku 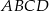 zaznaczono dowolny punkt
zaznaczono dowolny punkt 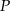 . Udowodnij, że pola trójkątów
. Udowodnij, że pola trójkątów 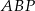 i
i  są równe.
są równe.

