Podaj wartość wyrażenia 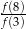 jeżeli
jeżeli 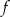 jest funkcją kwadratową o miejscach zerowych 2 i 4.
jest funkcją kwadratową o miejscach zerowych 2 i 4.
/Szkoła średnia/Funkcje/Kwadratowa/Różne
Miejscami zerowymi funkcji kwadratowej 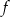 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 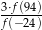 .
.
Liczby 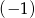 i 3 są miejscami zerowymi funkcji kwadratowej
i 3 są miejscami zerowymi funkcji kwadratowej 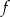 . Oblicz
. Oblicz 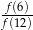 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 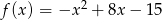 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 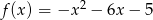 .
.
Wielomiany 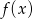 i
i 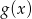 spełniają warunki
spełniają warunki 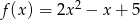 i
i 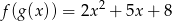 . Wyznacz wzór wielomianu
. Wyznacz wzór wielomianu 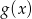 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 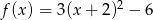 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 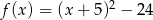 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 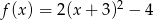 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 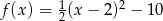 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 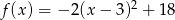 .
.
Zapisz wzór funkcji kwadratowej 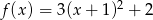 w postaci ogólnej.
w postaci ogólnej.
Sprowadź do postaci ogólnej funkcję kwadratową 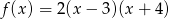 .
.
Wyznacz 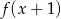 jeżeli
jeżeli 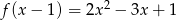 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 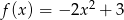 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 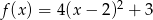 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 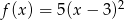 .
.
Zapisz wzór funkcji 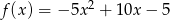 w postaci kanonicznej i iloczynowej.
w postaci kanonicznej i iloczynowej.
Zapisz wzór funkcji 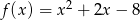 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 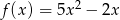 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 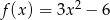 w postaci iloczynowej.
w postaci iloczynowej.
Zbadaj, na podstawie definicji, monotoniczność funkcji 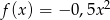 w zbiorze
w zbiorze 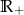 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 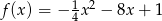 w zbiorze
w zbiorze 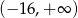 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 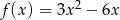 w zbiorze
w zbiorze 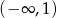 .
.
W poniższej tabeli podane są wartości funkcji kwadratowej 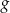 dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
| x | -2 | -1 | 0 | 1 | |
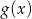 | -4 | 1 | 2 | -1 |
- Wyznacz wzór funkcji
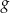 .
. - Uzupełnij brakujące zapisy w tabeli.
- Rozwiąż nierówność
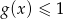 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 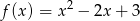 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 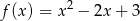 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 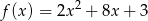 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 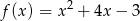 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 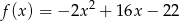 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 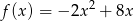 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci iloczynowej wzorem 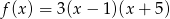 .
.
Dany jest trójmian kwadratowy 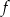 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 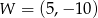 . Oblicz
. Oblicz 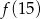 .
.
Funkcja kwadratowa 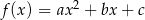 , spełnia warunek
, spełnia warunek 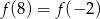 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  , spełniony jest warunek
, spełniony jest warunek 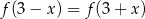 .
.
Wyznacz wartość funkcji 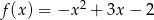 dla argumentu
dla argumentu 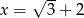 .
.
Wyznacz wartość funkcji 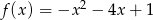 dla
dla 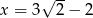 .
.

