Dane jest równanie 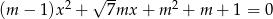 z niewiadomą
z niewiadomą  . Sporządź wykres funkcji
. Sporządź wykres funkcji 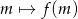 , gdzie
, gdzie 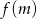 oznacza liczbę rzeczywistych pierwiastków danego równania.
oznacza liczbę rzeczywistych pierwiastków danego równania.
/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Liczba pierwiastków
Dla jakich wartości parametru 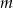 równanie
równanie 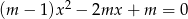 posiada 2 różne rozwiązania?
posiada 2 różne rozwiązania?
Wyznacz te wartości parametru 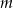 , dla których prosta
, dla których prosta 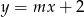 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 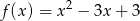 .
.
Wyznacz te wartości parametru 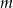 , dla których prosta
, dla których prosta 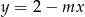 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 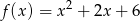 .
.
Wyznacz te wartości parametru 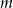 , dla których prosta
, dla których prosta 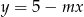 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 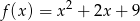 .
.
Wyznacz te wartości parametru 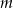 , dla których prosta
, dla których prosta 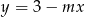 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 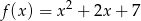 .
.
Wyznacz te wartości parametru 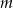 , dla których prosta
, dla których prosta 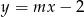 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 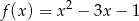 .
.
Wyznacz te wartości parametru 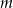 , dla których prosta
, dla których prosta 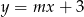 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 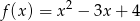 .
.
Dla jakich wartości parametru 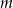 równanie
równanie 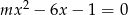 ma co najmniej jedno rozwiązanie?
ma co najmniej jedno rozwiązanie?
Znajdź zbiór tych wartości parametru 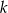 , dla których dane równanie ma dwa różne pierwiastki
, dla których dane równanie ma dwa różne pierwiastki 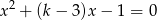 .
.
Dane jest równanie 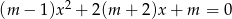 z niewiadomą
z niewiadomą  .
.
- Zbadaj liczbę pierwiastków równania w zależności od wartości parametru
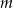 .
. - Dla jakich wartości parametru
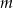 zachodzi nierówność
zachodzi nierówność 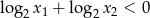 , gdzie
, gdzie 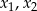 są różnymi pierwiastkami danego równania.
są różnymi pierwiastkami danego równania.
Wyznacz te wartości parametru 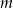 , dla których równanie
, dla których równanie 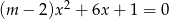 ma jedno rozwiązanie.
ma jedno rozwiązanie.
Dla jakich 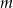 równanie
równanie 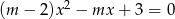 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Przedyskutuj liczbę rozwiązań równania 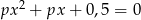 w zależności od wartości parametru
w zależności od wartości parametru 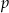 , a następnie naszkicuj wykres funkcji
, a następnie naszkicuj wykres funkcji 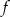 , która każdej wartości parametru
, która każdej wartości parametru 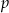 przyporządkowuje liczbę rozwiązań tego równania.
przyporządkowuje liczbę rozwiązań tego równania.
Wyznacz te wartości parametru 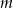 , dla których równanie
, dla których równanie 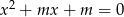 ma jedno rozwiązanie.
ma jedno rozwiązanie.
Określ liczbę pierwiastków równania 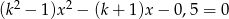 w zależności od wartości parametru
w zależności od wartości parametru 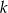 .
.
Wyznacz taki współczynnik 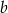 aby funkcja
aby funkcja 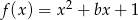 miała jedno miejsce zerowe.
miała jedno miejsce zerowe.
Wyznacz taki współczynnik 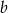 aby funkcja
aby funkcja 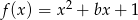 miała co najwyżej jedno miejsce zerowe.
miała co najwyżej jedno miejsce zerowe.
Wyznacz taki współczynnik 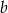 aby funkcja
aby funkcja 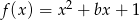 miała dwa miejsca zerowe.
miała dwa miejsca zerowe.
Określ liczbę pierwiastków równania 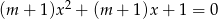 w zależności od wartości parametru
w zależności od wartości parametru 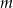 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

Naszkicuj wykres funkcji, która każdej liczbie rzeczywistej 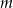 przyporządkowuje liczbę pierwiastków równania
przyporządkowuje liczbę pierwiastków równania
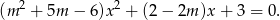
Wyznacz wszystkie wartości parametru 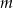 , dla których prosta o równaniu
, dla których prosta o równaniu 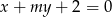 ma dokładnie dwa punkty wspólne z parabolą o równaniu
ma dokładnie dwa punkty wspólne z parabolą o równaniu 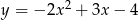 .
.
Zbadaj liczbę rozwiązań równania ze względu na wartość parametru 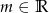 . Napisz wzór i narysuj wykres funkcji
. Napisz wzór i narysuj wykres funkcji 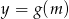 , która każdej wartości parametru
, która każdej wartości parametru 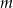 przyporządkowuje liczbę rozwiązań równania
przyporządkowuje liczbę rozwiązań równania 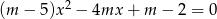 .
.

