Wyznacz cztery kolejne liczby całkowite takie, że sześcian największej z nich jest równy sumie sześcianów trzech pozostałych liczb.
/Szkoła średnia/Zadania z treścią/Własności liczb/Różne
Iloczyn trzech kolejnych liczb nieparzystych jest o 65 większy od różnicy kwadratów liczby największej i najmniejszej. Znajdź te liczby.
Suma dwóch liczb jest równa 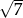 , a ich różnica
, a ich różnica 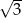 . Oblicz iloczyn tych liczb.
. Oblicz iloczyn tych liczb.
Różnica kwadratów dwóch kolejnych liczb naturalnych wynosi 13. Wyznacz te liczby.
Różnica kwadratów dwóch kolejnych liczb naturalnych wynosi 17. Wyznacz te liczby.
Suma dwóch liczb, ich iloczyn i różnica ich kwadratów są równe. Wyznacz te liczby.
Suma stu kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 2 wynosi 30950. Wyznacz najmniejszą i największą z tych liczb.
Różnica dwóch liczb naturalnych dodatnich mniejszych od 160 jest równa 119, a ich największy wspólny dzielnik jest równy 17. Wyznacz te liczby.
Różnica dwóch liczb naturalnych dodatnich mniejszych od 130 jest równa 98, a ich największy wspólny dzielnik jest równy 14. Wyznacz te liczby.
Suma sześcianów trzech kolejnych liczb całkowitych wynosi -36. Wyznacz te liczby.
Suma ilu kolejnych liczb naturalnych wynosi 300?
Wyznacz wszystkie liczby rzeczywiste, które są o 2 większe od swojej odwrotności.
Wyznacz cztery kolejne liczby całkowite takie, że największa z nich jest równa sumie kwadratów trzech pozostałych liczb.
Suma dwóch liczb jest równa 7 i jest o 2 mniejsza od ich iloczynu. Wyznacz te liczby.
Liczba  jest o 3 większa od liczby
jest o 3 większa od liczby 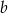 . Iloraz liczb
. Iloraz liczb  i
i 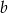 jest dwa razy mniejszy od sumy tych liczb. Wyznacz liczby
jest dwa razy mniejszy od sumy tych liczb. Wyznacz liczby  i
i 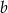 .
.
Podaj przykład liczb naturalnych  i
i 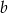 takich, że
takich, że 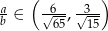 .
.
Liczbę 42 przedstaw w postaci sumy dwóch składników tak, by różnica ich kwadratów była równa 168.
Dane są dwie liczby dodatnie  i
i 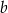 , których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia:
, których stosunek wynosi 4:5. Jeżeli mniejszą z tych liczb zwiększymy o 25%, a większą zmniejszymy o 40, to stosunek otrzymanych liczb wyniesie 3:2. Oblicz wartość wyrażenia: 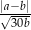 .
.
Dane są dwie liczby dodatnie  i
i 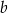 , których stosunek wynosi 3:5. Jeżeli mniejszą z tych liczb zwiększymy o 18, a większą zmniejszymy o 55%, to stosunek otrzymanych liczb wyniesie 8:5. Oblicz wartość wyrażenia:
, których stosunek wynosi 3:5. Jeżeli mniejszą z tych liczb zwiększymy o 18, a większą zmniejszymy o 55%, to stosunek otrzymanych liczb wyniesie 8:5. Oblicz wartość wyrażenia: 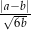 .
.
Licznik ułamka jest o 3 mniejszy od mianownika. Jeżeli do tego ułamka dodamy jego odwrotność to otrzymamy 2,9. Znaleźć ten ułamek.
Mianownik ułamka jest dodatni i o 1 większy od licznika. Jeżeli do tego ułamka dodamy jego odwrotność to otrzymamy 2,05. Wyznacz ten ułamek.
Znajdź ułamek o mianowniku 4 leżący na osi liczbowej między 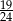 a
a  .
.
Znajdź ułamek o mianowniku 5 leżący na osi liczbowej między 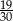 a
a 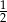 .
.
Suma dwóch kolejnych liczb naturalnych jest większa od 36, a suma kwadratów tych liczb jest mniejsza od 841. Znajdź te liczby.
Suma kwadratów trzech kolejnych liczb naturalnych wynosi 149. Wyznacz te liczby.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy połowę jego licznika, to otrzymamy 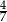 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 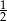 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 45, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 3, to otrzymamy liczbę 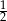 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Dany jest dodatni ułamek nieskracalny. Jeżeli dodamy do licznika ułamka 20% mianownika, a następnie od mianownika odejmiemy 20% zmienionego licznika, to otrzymamy 1,25. Jeżeli natomiast do mianownika danego ułamka dodamy 25% licznika, a od licznika odejmiemy 1, to otrzymamy 0,5. Wyznacz ten ułamek.
Jeżeli do licznika pewnego nieskracalnego ułamka dodamy 32, a mianownik pozostawimy niezmieniony, to otrzymamy liczbę 2. Jeżeli natomiast od licznika i od mianownika tego ułamka odejmiemy 6, to otrzymamy liczbę 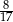 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy 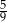 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika dodatniego ułamka dodamy jego licznik, to otrzymamy  , a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy 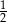 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.
Jeżeli do licznika i do mianownika nieskracalnego dodatniego ułamka dodamy jego licznik, to otrzymamy 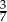 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 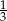 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.

