Dla jakich wartości parametru 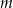 równanie
równanie 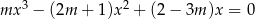 ma rozwiązania, których suma jest dodatnia?
ma rozwiązania, których suma jest dodatnia?
/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem
Wyznacz wszystkie wartości parametru 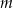 , dla których równanie
, dla których równanie
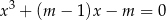
ma dokładnie dwa pierwiastki rzeczywiste. Dla otrzymanych wartości 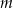 wyznacz te pierwiastki.
wyznacz te pierwiastki.
Wielomian 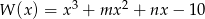 ma trzy pierwiastki
ma trzy pierwiastki 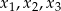 , przy czym
, przy czym 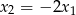 i
i 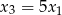 . Wyznacz
. Wyznacz 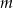 i
i  .
.
Wielomian 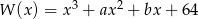 ma trzy pierwiastki:
ma trzy pierwiastki: 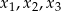 , przy czym
, przy czym 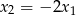 i
i 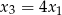 . Wyznacz
. Wyznacz  i
i 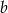 .
.
Równanie 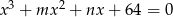 ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie
ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie 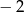 . Wyznacz
. Wyznacz 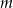 i
i  .
.
Liczba 3 jest pierwiastkiem wielomianu 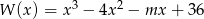 . Wyznacz parametr
. Wyznacz parametr 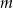 i pozostałe pierwiastki tego wielomianu.
i pozostałe pierwiastki tego wielomianu.
Wielomian 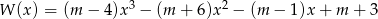 jest podzielny przez dwumian
jest podzielny przez dwumian 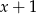 . Dla jakich wartości parametru
. Dla jakich wartości parametru 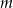 wielomian
wielomian 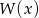 ma dokładnie dwa pierwiastki?
ma dokładnie dwa pierwiastki?
Wiedząc, że suma kwadratów pierwiastków równania
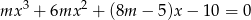
jest równa 30, wyznacz 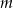 .
.
Sprawdź dla jakiego 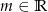 pierwiastki wielomianu
pierwiastki wielomianu 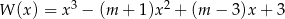 tworzą ciąg arytmetyczny?
tworzą ciąg arytmetyczny?
Wyznacz wszystkie wartości parametru 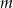 , dla których jedynym rozwiązaniem rzeczywistym równania
, dla których jedynym rozwiązaniem rzeczywistym równania 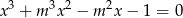 jest liczba 1.
jest liczba 1.
Pierwiastkiem wielomianu 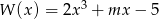 jest liczba -2. Wyznacz parametr
jest liczba -2. Wyznacz parametr 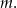
Pierwiastkiem wielomianu 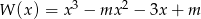 jest liczba
jest liczba 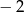 . Wyznacz parametr
. Wyznacz parametr 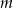 .
.
Dane są liczby wymierne 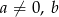 i
i 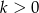 takie, że liczby
takie, że liczby 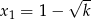 i
i 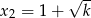 są pierwiastkami równania
są pierwiastkami równania 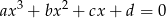 . Wykaż, że
. Wykaż, że  i
i 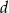 są liczbami wymiernymi.
są liczbami wymiernymi.
Dany jest wielomian 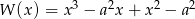 , gdzie
, gdzie 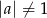 .
.
- Oblicz sumę pierwiastków tego wielomianu.
- Wyznacz wartość parametru
 , dla której suma kwadratów pierwiastków wielomianu
, dla której suma kwadratów pierwiastków wielomianu 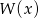 jest możliwie najmniejsza.
jest możliwie najmniejsza.
Dany jest wielomian 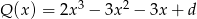 .
.
- Liczba 1 jest pierwiastkiem tego wielomianu. Oblicz
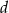 .
. - Dla
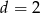 przedstaw wielomian
przedstaw wielomian 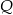 w postaci iloczynu wielomianów stopnia pierwszego.
w postaci iloczynu wielomianów stopnia pierwszego.
Wyznacz współczynniki  i
i 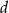 wielomianu
wielomianu 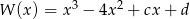 wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu
wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu 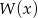 .
.
Jedynym rozwiązaniem wymiernym równania 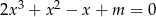 , gdzie
, gdzie 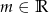 , jest liczba
, jest liczba 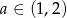 . Wyznacz liczbę
. Wyznacz liczbę 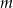 oraz pozostałe pierwiastki wielomianu.
oraz pozostałe pierwiastki wielomianu.
Udowodnij, że jeżeli wielomian 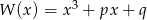 ma trzy pierwiastki, to
ma trzy pierwiastki, to 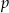 jest liczbą ujemną.
jest liczbą ujemną.
Dla jakich wartości parametru 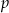 wielomian
wielomian 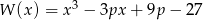 ma trzy różne pierwiastki rzeczywiste?
ma trzy różne pierwiastki rzeczywiste?
Wyznacz wszystkie wartości parametru 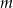 , dla którego wielomian
, dla którego wielomian 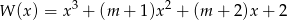 ma trzy różne pierwiastki rzeczywiste.
ma trzy różne pierwiastki rzeczywiste.
Wyznacz wszystkie wartości parametru 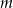 , dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu
, dla których liczba 1 jest jedynym całkowitym pierwiastkiem wielomianu 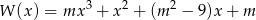 .
.
Wyznacz wszystkie wartości parametru 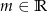 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 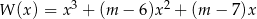 tworzą ciąg arytmetyczny.
tworzą ciąg arytmetyczny.
Wyznacz wszystkie wartości parametru 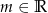 , dla których równanie
, dla których równanie
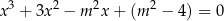
ma trzy różne pierwiastki, z których jeden jest ujemny, a pozostałe dwa należą do przedziału ![[ ] 1 2 ,5](https://img.zadania.info/zad/4913698/HzadT2x.png) .
.
Dla jakich wartości parametru 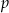 wielomian
wielomian 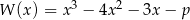 ma trzy pierwiastki rzeczywiste?
ma trzy pierwiastki rzeczywiste?
Dany jest wielomian 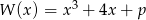 , gdzie
, gdzie 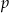 jest liczbą pierwszą. Wyznacz
jest liczbą pierwszą. Wyznacz 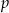 wiedząc, że
wiedząc, że 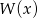 ma pierwiastek całkowity.
ma pierwiastek całkowity.

