Granica 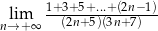 jest równa
jest równa
A) 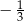 B)
B) 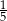 C)
C) 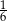 D) 0
D) 0
/Szkoła średnia/Zadania testowe/Ciągi/Granice
Granica 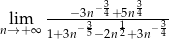 jest równa
jest równa
A) 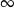 B)
B) 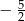 C) 0 D)
C) 0 D) 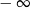
Nieskończony ciąg liczbowy jest określony wzorem 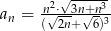 dla
dla 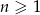 . Wtedy
. Wtedy
A) 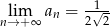 B)
B) 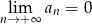 C)
C) 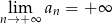 D)
D) 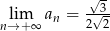
Granice 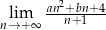 i
i 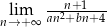 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 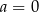 i
i 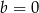 B)
B) 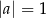 i
i 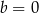 C)
C) 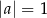 i
i 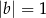 D)
D) 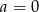 i
i 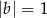
Granice 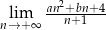 i
i 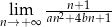 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 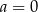 i
i 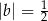 B)
B) 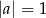 i
i 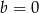 C)
C) 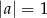 i
i 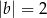 D)
D) 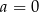 i
i 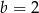
Granice 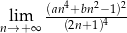 i
i 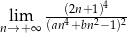 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 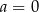 i
i 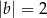 B)
B) 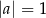 i
i 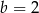 C)
C) 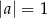 i
i 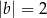 D)
D) 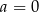 i
i 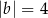
Jeżeli 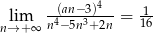 , to liczba
, to liczba  może być równa
może być równa
A) 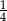 B)
B) 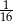 C)
C) 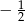 D) 2
D) 2
Jeżeli 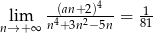 , to liczba
, to liczba  może być równa
może być równa
A) 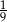 B)
B) 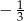 C)
C) 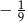 D) 3
D) 3
Granica 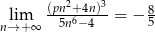 . Wynika stąd, że
. Wynika stąd, że
A) 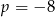 B)
B) 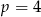 C)
C) 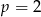 D)
D) 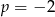
Jeżeli 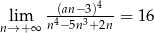 , to liczba
, to liczba  może być równa
może być równa
A) 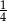 B)
B) 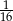 C)
C) 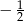 D) 2
D) 2
Granica 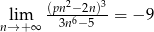 . Wynika stąd, że
. Wynika stąd, że
A) 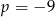 B)
B) 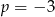 C)
C) 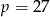 D)
D) 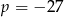
Jeżeli 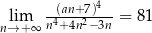 , to liczba
, to liczba  może być równa
może być równa
A) 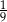 B)
B) 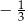 C)
C) 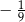 D) 3
D) 3
Granica 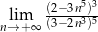 jest równa
jest równa
A) 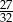 B)
B) 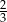 C)
C) 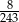 D)
D) 
Granica 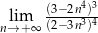 jest równa
jest równa
A) 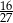 B)
B) 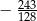 C)
C) 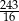 D)
D) 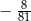
Ciąg 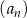 jest określony wzorem
jest określony wzorem 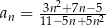 dla każdej liczby
dla każdej liczby 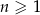 . Granica tego ciągu jest równa
. Granica tego ciągu jest równa
A) 3 B) 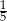 C)
C)  D)
D) 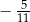
Ciąg 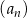 jest określony wzorem
jest określony wzorem 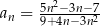 dla każdej liczby
dla każdej liczby 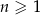 . Granica tego ciągu jest równa
. Granica tego ciągu jest równa
A) 5 B) 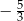 C)
C) 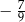 D)
D) 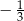
Granica 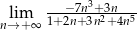 jest równa
jest równa
A) 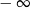 B)
B) 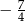 C) 0 D)
C) 0 D) 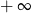
Granica 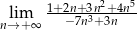 jest równa
jest równa
A) 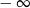 B)
B) 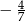 C) 0 D)
C) 0 D) 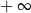
Nieskończony ciąg liczbowy jest określony wzorem 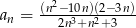 dla
dla 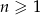 . Wtedy
. Wtedy
A) 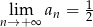 B)
B) 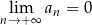 C)
C) 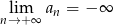 D)
D) 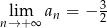
Nieskończony ciąg liczbowy jest określony wzorem 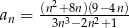 dla
dla 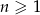 . Wtedy
. Wtedy
A) 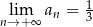 B)
B) 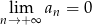 C)
C) 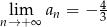 D)
D) 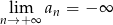
Granica ciągu 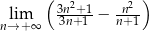 jest równa
jest równa
A) 1 B) 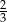 C)
C) 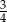 D)
D) 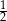
Granica ciągu 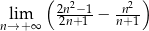 jest równa
jest równa
A) 1 B)  C)
C) 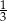 D)
D) 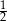
Granica 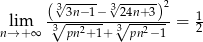 . Wynika stąd, że
. Wynika stąd, że
A) 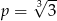 B)
B) 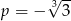 C)
C) 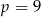 D)
D) 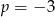
Granica
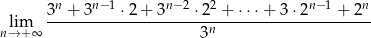
jest równa
A) 2 B) 3 C) 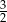 D) 0
D) 0
Granica ciągu 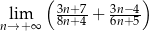 jest równa
jest równa
A) 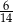 B)
B)  C)
C) 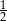 D)
D) 
Granica ciągu 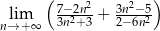 jest równa
jest równa
A) 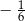 B)
B)  C)
C) 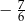 D)
D) 

