Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 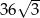 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 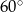 . Oblicz objętość stożka.
. Oblicz objętość stożka.
/Szkoła średnia/Geometria/Stereometria/Stożek/Objętość
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na łuku długości
. Kąt ten oparty jest na łuku długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
W kulę o promieniu 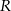 wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem
wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 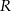 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 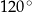 (zobacz rysunek). Oblicz objętość tego stożka.
(zobacz rysunek). Oblicz objętość tego stożka.

Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz stosunek objętości stożka do objętości wpisanej w niego kuli.
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni całkowitej. Oblicz stosunek objętości kuli wpisanej w stożek do objętości stożka.
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na cięciwie o długości
. Kąt ten oparty jest na cięciwie o długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Pole podstawy stożka jest równe 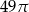 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 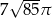 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Stożek, którego pole powierzchni bocznej jest równe 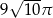 , jest wpisany w kulę o promieniu 5. Oblicz objętość stożka.
, jest wpisany w kulę o promieniu 5. Oblicz objętość stożka.
Wysokość stożka podzielono na trzy równe odcinki i przez punkty podziału poprowadzono płaszczyzny równoległe do podstawy. Oblicz stosunek objętości powstałych brył.
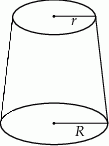
Przedstawiona na rysunku bryła to stożek ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 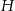 , a
, a  i
i 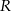 (
(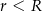 ) są promieniami podstaw. Oblicz objętość tej bryły.
) są promieniami podstaw. Oblicz objętość tej bryły.
W stożek w którym kąt między tworzącą, a podstawą ma miarę 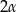 wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
wpisano kulę. Oblicz stosunek objętości stożka do objętości kuli.
Tworzącą stożka widać ze środka kuli wpisanej w ten stożek pod kątem o mierze  . Wyznacz stosunek objętości tej kuli do objętości stożka.
. Wyznacz stosunek objętości tej kuli do objętości stożka.
Oblicz objętość stożka wpisanego w kulę o promieniu 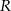 , wiedząc, że kąt rozwarcia stożka ma miarę
, wiedząc, że kąt rozwarcia stożka ma miarę 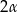 .
.
Podstawa stożka o kącie rozwarcia 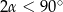 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu
jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu  .
.
Tworząca stożka o kącie rozwarcia  ma długość 8. Pole powierzchni całkowitej tego stożka jest równe
ma długość 8. Pole powierzchni całkowitej tego stożka jest równe 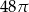 . Oblicz objętość stożka oraz miarę kąta
. Oblicz objętość stożka oraz miarę kąta  .
.
Tworząca stożka o kącie rozwarcia  ma długość 6. Pole powierzchni całkowitej tego stożka jest równe
ma długość 6. Pole powierzchni całkowitej tego stożka jest równe 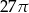 . Oblicz objętość stożka oraz miarę kąta
. Oblicz objętość stożka oraz miarę kąta  .
.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Pole powierzchni bocznej stożka jest trzy razy większe od pola jego podstawy. Wysokość tego stożka jest równa 12. Oblicz objętość tego stożka.
Do pojemnika w kształcie stożka wlano 1 litr wody, która wypełniła to naczynie do 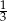 wysokości. Jaka jest całkowita pojemność tego naczynia?
wysokości. Jaka jest całkowita pojemność tego naczynia?
Dany jest stożek o polu powierzchni bocznej równym 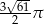 , w którym tangens kąta nachylenia tworzącej do podstawy jest równy
, w którym tangens kąta nachylenia tworzącej do podstawy jest równy  . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 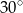 .
.

