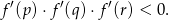Wykaż, że dla dowolnych liczb rzeczywistych 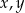 prawdziwa jest nierówność
prawdziwa jest nierówność
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych liczb rzeczywistych 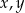 prawdziwa jest nierówność
prawdziwa jest nierówność
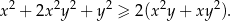
Wykaż, że dla dowolnych liczb rzeczywistych 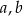 prawdziwa jest nierówność
prawdziwa jest nierówność
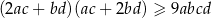
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 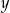 , spełniających warunek
, spełniających warunek 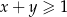 , prawdziwa jest nierówność
, prawdziwa jest nierówność
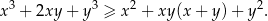
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 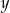 , spełniających warunek
, spełniających warunek 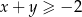 , prawdziwa jest nierówność
, prawdziwa jest nierówność
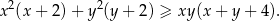
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 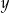 takich, że
takich, że 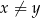 , spełniona jest nierówność
, spełniona jest nierówność
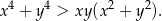
Udowodnij, że dla każdych dwóch liczb rzeczywistych 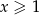 i
i 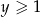 prawdziwa jest nierówność
prawdziwa jest nierówność
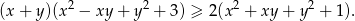
Udowodnij, że dla każdych dwóch liczb rzeczywistych 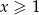 i
i 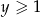 prawdziwa jest nierówność
prawdziwa jest nierówność
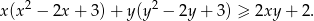
Wykaż, że dla wszystkich liczb rzeczywistych 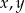 prawdziwa jest nierówność
prawdziwa jest nierówność 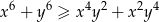 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 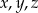 takich, że
takich, że 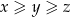 , prawdziwa jest nierówność
, prawdziwa jest nierówność
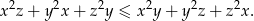
Możesz skorzystać z tożsamości
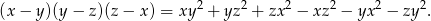
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 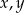 prawdziwa jest nierówność
prawdziwa jest nierówność
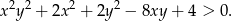
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 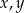 prawdziwa jest nierówność
prawdziwa jest nierówność
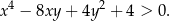
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 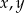 prawdziwa jest nierówność
prawdziwa jest nierówność
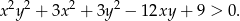
Wykaż, że dla dowolnych liczb rzeczywistych 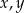 prawdziwa jest nierówność
prawdziwa jest nierówność
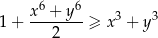
Dany jest wielomian 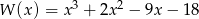 .
.
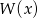 i
i 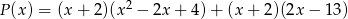 są równe.
są równe. 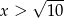 , to
, to 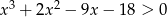 .
.Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
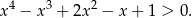
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
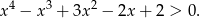
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
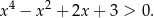
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
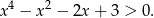
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
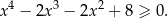
Wykaż, że dla dowolnych liczb rzeczywistych 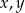 prawdziwa jest nierówność
prawdziwa jest nierówność
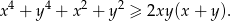
Udowodnij, że jeżeli 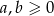 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 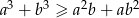 .
.
Wykaż, że dla wszystkich nieujemnych liczb rzeczywistych 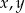 prawdziwa jest nierówność
prawdziwa jest nierówność 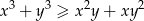 .
.
Funkcja 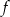 określona jest wzorem
określona jest wzorem 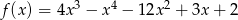 dla
dla 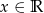 . Wykaż, że
. Wykaż, że
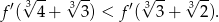
Wykaż, że dla dowolnych liczb rzeczywistych 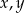 prawdziwa jest nierówność
prawdziwa jest nierówność
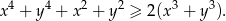
Wykaż, że dla dowolnych liczb rzeczywistych 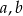 prawdziwa jest nierówność
prawdziwa jest nierówność
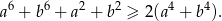
Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest nierówność
spełniona jest nierówność
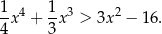
Udowodnij, że jeżeli 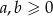 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 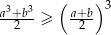 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 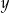 takich, że
takich, że 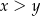 , spełniona jest nierówność
, spełniona jest nierówność
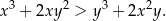
Wykaż, że dla dowolnych liczb rzeczywistych 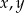 prawdziwa jest nierówność
prawdziwa jest nierówność
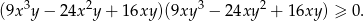
Funkcja 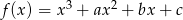 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 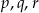 . Wykaż, że
. Wykaż, że