Punkty 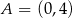 i
i 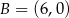 są końcami odcinka
są końcami odcinka 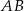 . Prosta
. Prosta 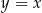 przecina odcinek
przecina odcinek 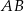 w punkcie
w punkcie 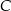 . Oblicz stosunek
. Oblicz stosunek 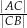 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Prostokątny
Punkty 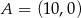 i
i 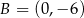 są końcami odcinka
są końcami odcinka 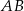 . Prosta
. Prosta 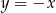 przecina odcinek
przecina odcinek 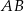 w punkcie
w punkcie 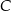 . Oblicz stosunek
. Oblicz stosunek 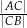 .
.
Wyznacz równanie takiej prostej przechodzącej przez punkt 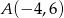 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
Dane są punkty 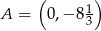 i
i 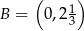 . Wyznacz na prostej
. Wyznacz na prostej 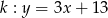 punkt
punkt 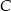 , tak aby
, tak aby 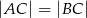 . Dla wyznaczonego punktu C:
. Dla wyznaczonego punktu C:
- wykaż, że trójkąt
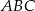 jest prostokątny;
jest prostokątny; - wyznacz równanie okręgu opisanego na trójkącie
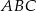 .
.
Punkt 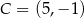 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 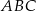 , w którym
, w którym 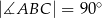 i
i 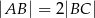 . Prosta
. Prosta 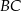 ma równanie
ma równanie 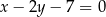 , a punkt
, a punkt 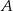 leży na prostej
leży na prostej 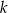 o równaniu
o równaniu 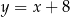 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 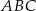 .
.
Punkt 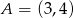 jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym
jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym 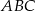 . Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu
. Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu 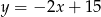 . Wyznacz współrzędne pozostałych wierzchołków trójkąta
. Wyznacz współrzędne pozostałych wierzchołków trójkąta 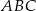 .
.
W równoramiennym trójkącie prostokątnym punkt 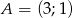 jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu
jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu 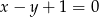 . Napisz równania prostych zawierających pozostałe boki trójkąta.
. Napisz równania prostych zawierających pozostałe boki trójkąta.
Znajdź równanie prostej 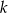 przechodzącej przez punkt
przechodzącej przez punkt 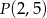 , która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
, która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
Punkt 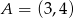 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 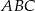 , o kącie prostym
, o kącie prostym 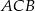 , a
, a 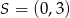 jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że
jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że 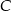 należy do ujemnej części osi
należy do ujemnej części osi 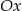 .
.
Na rysunku prosta 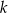 przechodzi przez punkt
przechodzi przez punkt 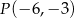 .
.
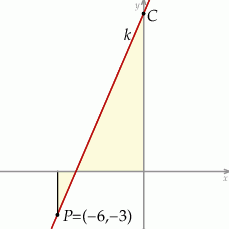
Wiedząc, że stosunek pól zacieniowanych trójkątów prostokątnych jest równy 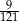
- oblicz pola tych trójkątów;
- wyznacz równanie prostej
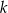 .
.
Punkty 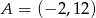 i
i 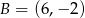 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 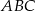 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 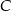 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 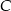 tego trójkąta, wiedząc, że leży on na prostej o równaniu
tego trójkąta, wiedząc, że leży on na prostej o równaniu 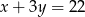 . Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
. Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
W trójkącie prostokątnym 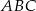 o przeciwprostokątnej
o przeciwprostokątnej 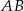 dane są wierzchołki
dane są wierzchołki 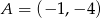 i
i 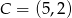 . Punkt
. Punkt 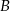 leży na prostej o równaniu
leży na prostej o równaniu 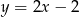 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.
Dwa boki trójkąta prostokątnego 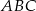 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 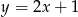 oraz
oraz 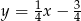 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 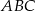 jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt
jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt 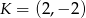 . Rozważ wszystkie możliwości.
. Rozważ wszystkie możliwości.
Punkty 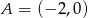 i
i 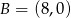 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 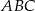 o przeciwprostokątnej
o przeciwprostokątnej 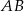 i polu równym 15. Oblicz współrzędne punktu
i polu równym 15. Oblicz współrzędne punktu 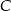 .
.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego 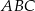 :
: 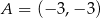 i
i 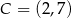 oraz prosta o równaniu
oraz prosta o równaniu 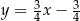 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 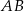 tego trójkąta.
tego trójkąta.
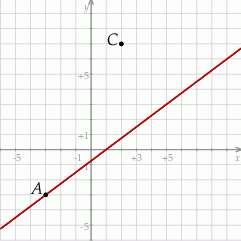
Oblicz współrzędne wierzchołka 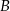 tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 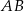 .
.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego 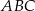 :
: 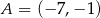 i
i 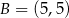 oraz prosta o równaniu
oraz prosta o równaniu 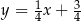 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 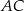 tego trójkąta.
tego trójkąta.
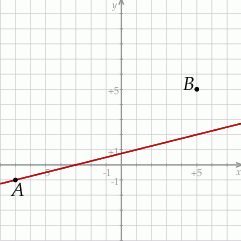
Oblicz współrzędne wierzchołka 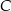 tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 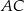 .
.
Przyprostokątna 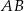 trójkąta prostokątnego
trójkąta prostokątnego 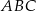 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 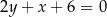 , a środek jego przeciwprostokątnej
, a środek jego przeciwprostokątnej 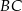 ma współrzędne
ma współrzędne 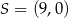 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 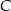 jeżeli
jeżeli 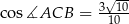 .
.
Punkty 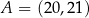 i
i 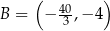 są końcami przeciwprostokątnej trójkąta prostokątnego
są końcami przeciwprostokątnej trójkąta prostokątnego 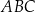 . Punkt
. Punkt 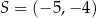 jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta
jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta 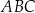 .
.
Punkty 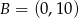 i
i 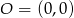 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 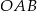 , w którym
, w którym 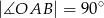 . Przyprostokątna
. Przyprostokątna 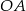 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 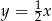 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 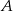 i długość przyprostokątnej
i długość przyprostokątnej 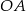 .
.
Wierzchołki 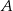 i
i 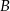 trójkąta prostokątnego
trójkąta prostokątnego 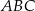 leżą na osi
leżą na osi 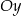 układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków
układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków 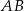 ,
, 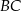 i
i 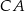 w punktach – odpowiednio –
w punktach – odpowiednio – 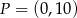 ,
, 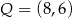 i
i 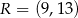 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 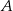 ,
, 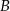 i
i 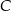 tego trójkąta.
tego trójkąta.
Wierzchołki 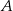 i
i 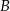 trójkąta prostokątnego
trójkąta prostokątnego 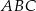 leżą na prostej
leżą na prostej 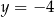 . Okrąg wpisany w ten trójkąt jest styczny do boków
. Okrąg wpisany w ten trójkąt jest styczny do boków 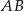 ,
, 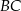 i
i 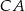 odpowiednio w punktach
odpowiednio w punktach 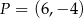 ,
, 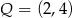 i
i 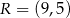 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 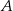 ,
, 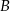 i
i 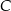 tego trójkąta.
tego trójkąta.
W trójkącie prostokątnym 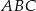 , gdzie
, gdzie 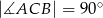 , wierzchołek
, wierzchołek 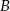 ma współrzędne
ma współrzędne 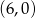 . Prosta
. Prosta 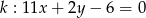 , zawierająca środkową trójkąta poprowadzoną z wierzchołka
, zawierająca środkową trójkąta poprowadzoną z wierzchołka 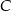 , przecina bok
, przecina bok 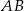 trójkąta w punkcie
trójkąta w punkcie 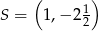 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 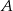 i
i 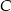 .
.
Wyznacz równanie symetralnej przeciwprostokątnej trójkąta prostokątnego o wierzchołkach 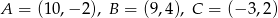 .
.

