Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 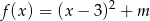 , gdzie
, gdzie 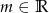 – parametr.
– parametr.
/Szkoła średnia/Geometria/Geometria analityczna/Miejsca geometryczne punktów
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 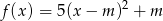 , gdzie
, gdzie 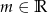 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 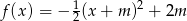 , gdzie
, gdzie 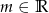 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 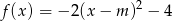 , gdzie
, gdzie 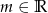 – parametr.
– parametr.
Dana jest prosta 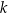 o równaniu
o równaniu 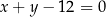 oraz punkt
oraz punkt 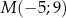 wyznacz na prostej
wyznacz na prostej 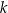 takie punkty
takie punkty 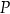 i
i 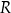 aby
aby 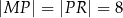 .
.
Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu 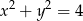 i stycznych do prostej o równaniu
i stycznych do prostej o równaniu 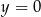 .
.
Punkty 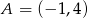 oraz
oraz 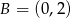 należą do prostej
należą do prostej 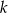 . Punkt
. Punkt 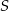 ma współrzędne
ma współrzędne 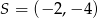 . Oblicz współrzędne punktów należących do prostej
. Oblicz współrzędne punktów należących do prostej 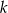 , których odległość od punktu
, których odległość od punktu 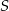 wynosi 5.
wynosi 5.
Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach 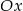 i
i 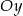 układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
Wyznacz figurę, która jest zbiorem środków cięciw paraboli 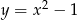 przechodzących przez początek układu współrzędnych.
przechodzących przez początek układu współrzędnych.
Dana jest prosta 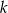 o równaniu
o równaniu 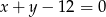 oraz punkt
oraz punkt 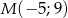 wyznacz na prostej
wyznacz na prostej 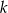 takie punkty
takie punkty 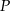 i
i 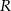 aby
aby 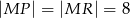 .
.
Na prostej 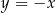 wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu
wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu 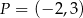 .
.
Dane są dwa punkty 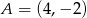 i
i 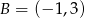 oraz prosta
oraz prosta 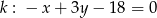 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 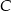 leżącego na prostej
leżącego na prostej 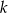 i tak samo odległego od punktów
i tak samo odległego od punktów 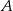 i
i 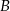 .
.
Dane są dwa punkty 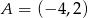 i
i 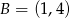 oraz prosta
oraz prosta 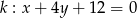 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 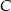 leżącego na prostej
leżącego na prostej 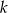 i tak samo odległego od punktów
i tak samo odległego od punktów 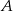 i
i 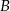 .
.
W układzie współrzędnych dane są punkty 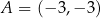 ,
, 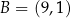 i
i 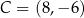 . Wyznacz wszystkie punkty
. Wyznacz wszystkie punkty 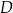 prostej
prostej 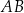 , które są różne od punktów
, które są różne od punktów 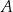 i
i 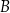 , i dla których suma pól trójkątów
, i dla których suma pól trójkątów 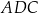 i
i 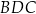 jest mniejsza od 120.
jest mniejsza od 120.
Wyznacz równanie zbioru środków wszystkich okręgów stycznych zewnętrznie do okręgu 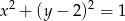 i stycznych do prostej
i stycznych do prostej 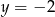 .
.
Znajdź zbiór środków wszystkich cięciw okręgu 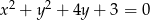 , wyznaczonych przez proste przechodzące przez punkt
, wyznaczonych przez proste przechodzące przez punkt 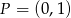 .
.
Dane są punkty 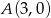 i
i 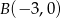 . Wyznacz równanie krzywej, utworzonej przez wszystkie punkty płaszczyzny, których odległość od punktu
. Wyznacz równanie krzywej, utworzonej przez wszystkie punkty płaszczyzny, których odległość od punktu 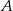 jest 2 razy większa od odległości od punktu
jest 2 razy większa od odległości od punktu 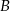 . Jaką figurę opisuje ta krzywa?
. Jaką figurę opisuje ta krzywa?
Dane są punkty 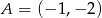 i
i 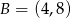 . Wyznacz te punkty prostej
. Wyznacz te punkty prostej 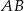 , dla których różnica odległości od punktu
, dla których różnica odległości od punktu 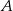 i odległości od punktu
i odległości od punktu 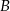 jest większa niż odległość od punktu
jest większa niż odległość od punktu 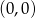 .
.
Oblicz, ile jest punktów 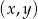 na płaszczyźnie, których współrzędne
na płaszczyźnie, których współrzędne  i
i 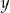 są liczbami całkowitymi spełniającymi odpowiednio nierówności:
są liczbami całkowitymi spełniającymi odpowiednio nierówności: 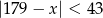 i
i 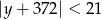 .
.
Narysuj w układzie współrzędnych zbiór
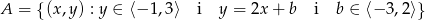
oraz oblicz jego pole powierzchni.
Dane są prosta 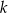 o równaniu
o równaniu 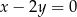 i prosta
i prosta 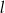 o równaniu
o równaniu 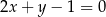 . Punkt
. Punkt 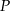 leży na prostej o równaniu
leży na prostej o równaniu 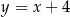 . Odległość punktu
. Odległość punktu 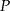 od prostej
od prostej 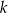 jest dwa razy większa niż odległość punktu
jest dwa razy większa niż odległość punktu 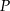 od prostej
od prostej 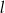 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 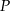 .
.
Dane są prosta 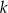 o równaniu
o równaniu 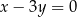 i prosta
i prosta 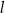 o równaniu
o równaniu 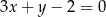 . Punkt
. Punkt 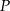 leży na prostej o równaniu
leży na prostej o równaniu 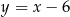 . Odległość punktu
. Odległość punktu 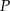 od prostej
od prostej 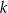 jest trzy razy większa niż odległość punktu
jest trzy razy większa niż odległość punktu 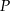 od prostej
od prostej 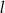 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 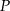 .
.
Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe od okręgu 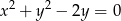 i od prostej
i od prostej 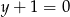 .
.

