Do sześciennego pudła o boku długości 60 cm, włożono walec, który jest styczny do przylegających ścian. Jak dużą kulkę można jeszcze zmieścić w wolnym rogu pudła?
/Szkoła średnia/Geometria/Stereometria/Sześcian/Różne
Punkty 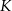 i
i 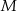 są środkami krawędzi
są środkami krawędzi 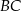 i
i 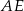 sześcianu
sześcianu 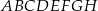 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 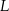 jest środkiem ściany
jest środkiem ściany 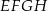 (zobacz rysunek). Oblicz obwód trójkąta
(zobacz rysunek). Oblicz obwód trójkąta 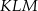 .
.
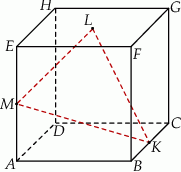
Dany jest sześcian 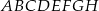 , w którym
, w którym 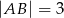 (patrz rysunek). Oblicz odległość wierzchołka
(patrz rysunek). Oblicz odległość wierzchołka 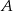 od przekątnej
od przekątnej 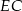 .
.
Dany jest sześcian 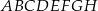 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 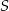 jest środkiem krawędzi
jest środkiem krawędzi 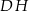 (zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta
(zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta 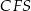 .
.
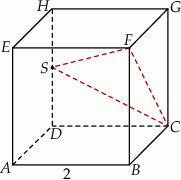
Punkty 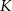 i
i 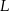 są środkami krawędzi
są środkami krawędzi 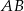 i
i 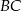 sześcianu
sześcianu 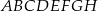 o krawędzi długości 1. Punkt
o krawędzi długości 1. Punkt 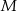 jest środkiem ściany
jest środkiem ściany 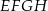 (zobacz rysunek). Oblicz pole trójkąta
(zobacz rysunek). Oblicz pole trójkąta 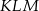 .
.
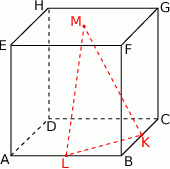
W sześcianie o krawędzi długości 2 połączono ze sobą środki trzech ścian mających wspólny wierzchołek. Sporządź odpowiedni rysunek i oblicz pole otrzymanego trójkąta.
Dany jest sześcian 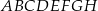 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 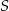 jest środkiem krawędzi
jest środkiem krawędzi 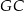 (zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie
(zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie 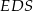 .
.
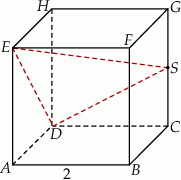
Dany jest sześcian 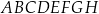 o krawędzi długości 1. Punkty
o krawędzi długości 1. Punkty 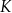 i
i 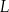 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 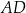 i
i 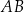 , a punkt
, a punkt 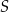 jest środkiem odcinka
jest środkiem odcinka 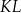 . Punkt
. Punkt 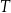 jest takim punktem krawędzi
jest takim punktem krawędzi 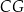 , że
, że 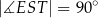 (zobacz rysunek).
(zobacz rysunek).
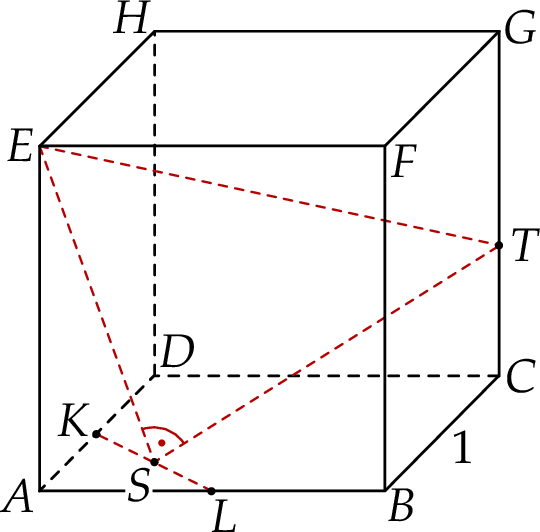
Oblicz odległość punktu 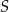 od środka odcinka
od środka odcinka 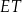 .
.
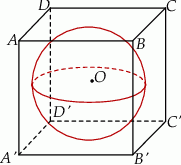
W sześcian o krawędzi 4 wpisano kulę styczną do trzech ścian sześcianu oraz przechodzącą przez środek sześcianu. Oblicz promień tej kuli.
Punkty 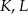 i
i 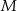 są środkami krawędzi
są środkami krawędzi 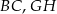 i
i 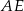 sześcianu
sześcianu 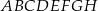 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 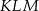 .
.
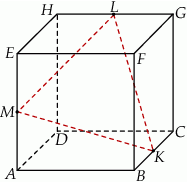
Na krawędziach sześcianu 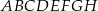 zaznaczono punkty
zaznaczono punkty 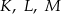 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 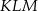 , jeśli krawędź sześcianu ma długość równą 4.
, jeśli krawędź sześcianu ma długość równą 4.
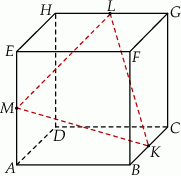
Na krawędziach sześcianu 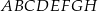 zaznaczono punkty
zaznaczono punkty 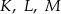 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 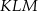 , jeśli krawędź sześcianu ma długość równą 2.
, jeśli krawędź sześcianu ma długość równą 2.
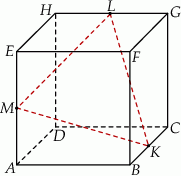
Punkty 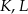 i
i 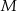 są środkami krawędzi
są środkami krawędzi 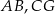 i
i 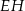 sześcianu
sześcianu 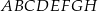 o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta
o krawędzi długości 1 (zobacz rysunek). Oblicz pole trójkąta 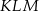 .
.
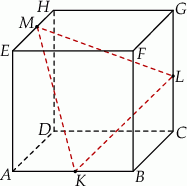
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
W narysowanym obok sześcianie krawędź ma długość  . Oblicz odległość wierzchołka
. Oblicz odległość wierzchołka 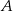 od płaszczyzny przechodzącej przez wierzchołki
od płaszczyzny przechodzącej przez wierzchołki 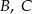 i
i 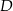 .
.
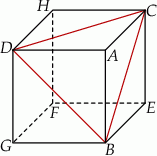
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.
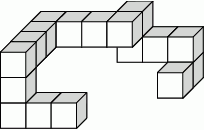
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?
Płaszczyzna 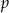 jest styczna do kuli wpisanej w sześcian
jest styczna do kuli wpisanej w sześcian 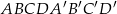 o krawędzi długości
o krawędzi długości 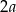 oraz przecina krawędzie
oraz przecina krawędzie 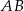 ,
, 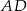 i
i 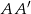 w takich punktach
w takich punktach 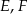 i
i 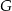 odpowiednio, że
odpowiednio, że 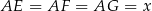 . Wykonaj odpowiedni rysunek i wyznacz
. Wykonaj odpowiedni rysunek i wyznacz  .
.
Oblicz odległość środka ściany sześcianu o krawędzi długości  od przekątnej tego sześcianu.
od przekątnej tego sześcianu.
Dany jest sześcian 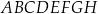 o krawędzi długości 6. Punkt
o krawędzi długości 6. Punkt 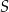 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 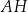 i
i 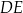 ściany bocznej
ściany bocznej 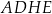 (zobacz rysunek).
(zobacz rysunek).
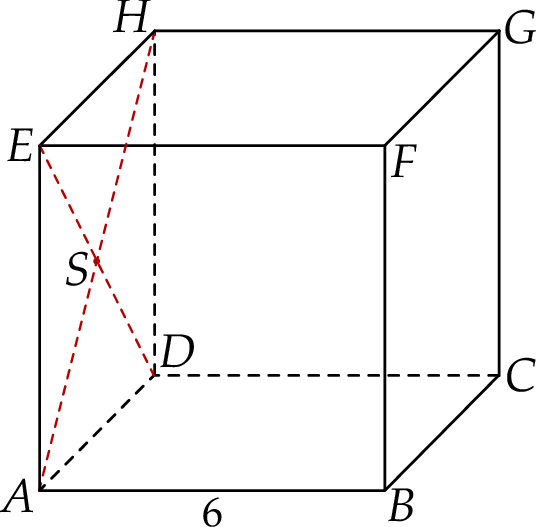
Oblicz wysokość trójkąta 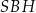 poprowadzoną z punktu
poprowadzoną z punktu 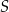 na bok
na bok 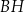 tego trójkąta.
tego trójkąta.
Dany jest sześcian 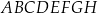 o krawędzi długości 3. Punkt
o krawędzi długości 3. Punkt 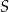 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 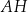 i
i 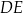 ściany bocznej
ściany bocznej 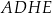 (zobacz rysunek).
(zobacz rysunek).
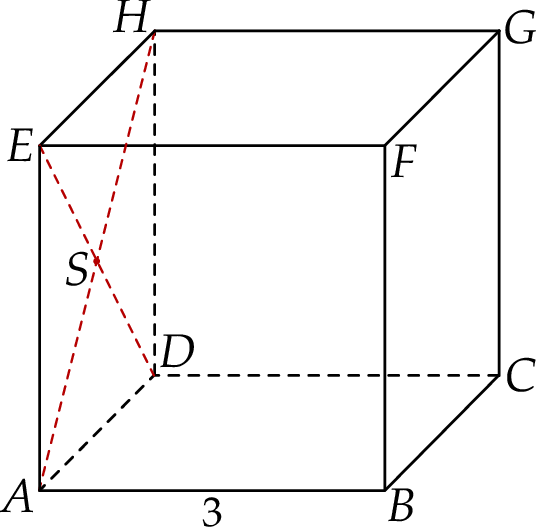
Oblicz wysokość trójkąta 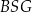 poprowadzoną z punktu
poprowadzoną z punktu 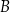 na bok
na bok  tego trójkąta.
tego trójkąta.
Jacek bawi się sześciennymi klockami o krawędzi 2 cm. Zbudował z nich jeden duży sześcian o krawędzi 8 cm i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Ania bawi się sześciennymi klockami o krawędzi 2 cm i buduje z nich bryły w kształcie prostokątów (prostopadłościanów o wysokości 1 klocka) w sposób przedstawiony na poniższym rysunku.
Najpierw Ania zbudowała z klocków pełen kwadrat o krawędzi 36 cm i wykorzystała do tego wszystkie swoje klocki. Następnie zburzyła tę budowlę i ułożyła z tych klocków prostokąt. Wtedy okazało się, że został jej dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej z ułożonych figur do pola powierzchni całkowitej drugiej figury.

