Wśród kilkuset studentów, którzy przystąpili do egzaminu z matematyki dokładnie jedna trzecia nie znała odpowiedzi na pierwsze pytanie. Egzaminator 10 razy wybrał z tej grupy studentów osobę i sprawdził czy zna odpowiedź na pierwsze pytanie (jedna osoba mogła zostać wybrana kilkukrotnie). Oblicz prawdopodobieństwo zdarzenia, że wśród tych wybranych 10 osób więcej niż połowa zna odpowiedź na pierwsze pytanie.
/Szkoła średnia/Prawdopodobieństwo/Schemat Bernoullego
Pogotowie ratunkowe dysponuje pewną liczbą karetek. W ciągu kilku miesięcy pracy stwierdzono, że w ciągu doby dana karetka będzie na miejscu w bazie z prawdopodobieństwem 0,4 jednakowym dla każdej karetki. Oblicz, ile karetek musi mieć do dyspozycji pogotowie, aby w razie wypadku, prawdopodobieństwo tego, że co najmniej jedna karetka jest na miejscu w bazie, było większe od 0,9.
Ukryj
Podobne zadania
Pan Nowak często gra z synem w szachy. Obliczył, że 40% rozegranych z synem partii wygrywa. Oblicz, ile partii szachów musi rozegrać z synem pan Nowak, aby prawdopodobieństwo wygrania przez ojca przynajmniej jednej partii w całej rozgrywce było większe od 0,95.
Wojtek i Łukasz postanowili rozegrać między sobą dziesięć partii gry w rzutki. Prawdopodobieństwo wygrania pojedynczej partii przez Wojtka jest trzy razy większe, niż prawdopodobieństwo wygrania partii przez Łukasza i każda partia kończy się zwycięstwem jednego z zawodników. Oblicz prawdopodobieństwo tego, że Wojtek nie wygrał wszystkich partii, ale wygrał ich co najmniej 7. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona 200 g herbaty. Torebkę, która zawiera mniej niż 200 g herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe 0,05. Oblicz, ile torebek herbaty należy poddać kontroli, aby prawdopodobieństwo otrzymania w kontrolowanej partii przynajmniej jednej torebki z niedowagą było większe niż 0,7.
Tomek i Romek postanowili rozegrać między sobą pięć partii szachów. Prawdopodobieństwo wygrania pojedynczej partii przez Tomka jest równe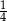 
. Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
Ukryj
Podobne zadania
Kasia i Ula grają w warcaby i każda rozgrywka kończy się wygraną jednej z dziewczynek. Prawdopodobieństwo wygrania pojedynczej partii przez Ulę jest równe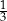 
. Oblicz prawdopodobieństwo wygrania przez Kasię co najmniej sześciu z siedmiu rozegranych partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona 200 g herbaty. Torebkę, która zawiera mniej niż 200 g herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe 0,1. Kontroli poddano masę herbaty w torebkach napełnianych przez tę maszynę danego dnia. Do kontroli wybrano losowo 20 torebek. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 20 losowo wybranych torebek znajdą się co najwyżej dwie torebki z niedowagą.
Ukryj
Podobne zadania
Maszyna napełnia butelki wodą, przy czym każda butelka ma zostać napełniona wodą do 750 ml objętości. Prawdopodobieństwo tego, że butelka zostanie napełniona prawidłowo wynosi 97%. Kontroli poddano partię 30 butelek napełnionych przez tę maszynę danego dnia. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród tych 30 losowo wybranych butelek znajdą się co najwyżej dwie butelki, które nie zostały prawidłowo napełnione.
W pewnym zakładzie mleczarskim śmietana produkowana jest w 200–gramowych opakowaniach. Prawdopodobieństwo zdarzenia, że w losowo wybranym opakowaniu śmietana zawiera mniej niż 36% tłuszczu, jest równe 0,01. Kontroli poddajemy 10 losowo wybranych opakowań ze śmietaną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród opakowań poddanych tej kontroli będzie co najwyżej jedno opakowanie ze śmietaną, która zawiera mniej niż 36% tłuszczu. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części tysięcznych.
Z trzech urn, w których jest po 2 kule białe i 3 czarne, wyjmujemy po jednej kuli i wkładamy do czwartej urny, w której była jedna kula biała. Losujemy teraz jedną kulę z czwartej urny. Oblicz prawdopodobieństwo, że z czwartej urny wyjmiemy białą kulę.
Rzucamy 
razy monetą symetryczną. Jakie jest prawdopodobieństwo, że orzeł wypadnie nieparzystą liczbę razy?
Rzucamy 7 razy dwiema monetami. Oblicz prawdopodobieństwo, że co najmniej 6 razy wyrzucimy dwie reszki.
Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.
Badania statystyczne pokazały, że średnio 13,9% zapałek jest wadliwych. Jakie jest prawdopodobieństwo, że w pudełku z 90 zapałkami są więcej niż 2 wadliwe?
Pracownik parkingu zanotował numery rejestracyjne piętnastu kolejnych samochodów, które wjechały na parking. Oblicz prawdopodobieństwo, że wśród tych piętnastu numerów rejestracyjnych co najwyżej 3 nie kończyły się cyfrą 7. Przyjmij, że każdy z numerów rejestracyjnych był zakończony cyfrą, i że wystąpienie każdej z dziesięciu cyfr na końcu numeru rejestracyjnego jest jednakowo prawdopodobne.
Egzamin składa się z 15 zadań zamkniętych. Do każdego zadania podano cztery odpowiedzi, z których tylko jedna okazuje się poprawna. Zdający zalicza egzamin, jeśli udzieli poprawnych odpowiedzi w co najmniej 11 zadaniach. Pewien student przystąpił nieprzygotowany do egzaminu i w każdym zadaniu wybierał losowo odpowiedź. Przyjmij, że w każdym zadaniu wybór każdej z odpowiedzi przez studenta jest równo prawdopodobny. Oblicz prawdopodobieństwo zdarzenia, że ten student zaliczył egzamin.
W dwunastu rzutach monetą cztery razy wypadł orzeł. Oblicz prawdopodobieństwo, że orzeł wypadł w piątym rzucie tej serii rzutów.
Rzucono trzema monetami 7 razy. Oblicz prawdopodobieństwo, że 4 razy wyrzucono 2 reszki.
Rzucono dziesięć razy kostką do gry. Oblicz prawdopodobieństwo, że już w pierwszym rzucie wypadła szóstka, jeśli w ogóle wypadły trzy szóstki.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,1. Oblicz prawdopodobieństwo zdarzenia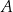 
polegającego na tym, że w okresie siedmiu dni wystąpią co najwyżej dwa takie dni, w których nastąpi awaria tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Ukryj
Podobne zadania
Prawdopodobieństwo wystąpienia awarii oświetlenia ulic w pewnym mieście w godzinach wieczornych pojedynczego dnia jest równe 0,2. Oblicz prawdopodobieństwo zdarzenia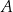 
polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Prawdopodobieństwo wystąpienia awarii sieci ciepłowniczej na pewnym osiedlu mieszkaniowym w godzinach porannych pojedynczego dnia jest równe 0,4. Oblicz prawdopodobieństwo zdarzenia 
polegającego na tym, że w okresie dziesięciu dni wystąpi 6, 7 lub 8 awarii tej sieci na tym osiedlu w godzinach porannych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Ile razy trzeba rzucać trzema monetami, aby prawdopodobieństwo otrzymania co najmniej raz jednocześnie trzech orłów było większe od 0,8?
Dwaj równorzędni przeciwnicy grają w szachy. Co jest bardziej prawdopodobne:
- wygranie dwóch partii z trzech, czy czterech partii z sześciu rozegranych?
- wygranie nie mniej niż dwóch partii z trzech, czy nie mniej niż czterech partii z sześciu rozegranych? (Remisów nie uwzględniamy.)
