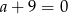Funkcja 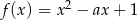 przyjmuje wartości mniejsze niż
przyjmuje wartości mniejsze niż 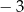 dla
dla
A) 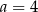 B)
B) 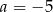 C)
C) 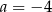 D)
D) 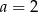
/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa/Z parametrem
Jeśli wykres funkcji kwadratowej 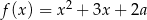 jest styczny do prostej
jest styczny do prostej 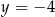 , to
, to
A) 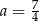 B)
B) 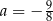 C)
C) 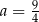 D)
D) 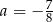
Jeśli wykres funkcji kwadratowej 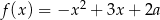 jest styczny do prostej
jest styczny do prostej 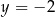 , to
, to
A) 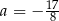 B)
B) 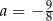 C)
C) 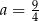 D)
D) 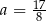
Funkcja 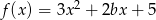 maleje w przedziale
maleje w przedziale 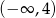 i rośnie w przedziale
i rośnie w przedziale 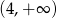 . Wynika stąd, że
. Wynika stąd, że
A) 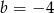 B)
B) 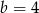 C)
C) 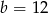 D)
D) 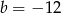
Funkcja 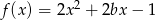 maleje w przedziale
maleje w przedziale 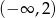 i rośnie w przedziale
i rośnie w przedziale 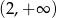 . Wynika stąd, że
. Wynika stąd, że
A) 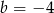 B)
B) 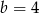 C)
C) 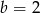 D)
D) 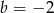
Funkcja 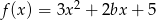 maleje w przedziale
maleje w przedziale 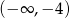 i rośnie w przedziale
i rośnie w przedziale 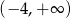 . Wynika stąd, że
. Wynika stąd, że
A) 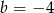 B)
B) 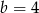 C)
C) 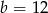 D)
D) 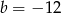
Funkcja kwadratowa określona jest wzorem 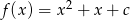 . Jeżeli
. Jeżeli 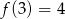 , to
, to
A) 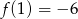 B)
B) 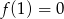 C)
C) 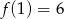 D)
D) 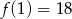
Funkcja kwadratowa określona jest wzorem 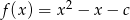 . Jeżeli
. Jeżeli 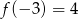 , to
, to
A) 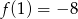 B)
B) 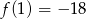 C)
C) 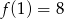 D)
D) 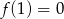
Funkcja kwadratowa określona jest wzorem 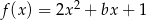 . Jeżeli
. Jeżeli 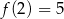 , to
, to
A) 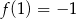 B)
B) 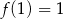 C)
C) 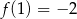 D)
D) 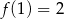
Funkcja kwadratowa określona jest wzorem 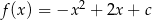 . Jeżeli
. Jeżeli 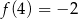 , to
, to
A) 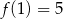 B)
B) 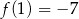 C)
C) 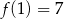 D)
D) 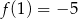
Funkcja kwadratowa określona jest wzorem 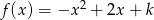 . Jeżeli
. Jeżeli 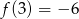 , to
, to
A) 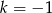 B)
B) 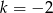 C)
C) 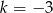 D)
D) 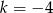
Zbiorem wartości funkcji kwadratowej 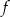 określonej wzorem
określonej wzorem 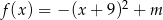 jest przedział
jest przedział 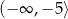 . Wtedy
. Wtedy
A) 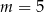 B)
B) 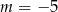 C)
C) 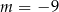 D)
D) 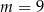
Zbiorem wartości funkcji kwadratowej 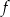 określonej wzorem
określonej wzorem 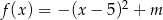 jest przedział
jest przedział 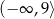 . Wtedy
. Wtedy
A) 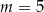 B)
B) 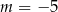 C)
C) 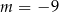 D)
D) 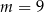
Zbiorem wartości funkcji 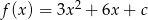 jest przedział
jest przedział 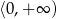 . Zatem współczynnik
. Zatem współczynnik  należy do zbioru
należy do zbioru
A) 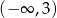 B)
B) 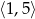 C)
C) 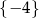 D)
D) 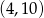
Zbiorem wartości funkcji kwadratowej 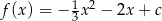 jest przedział
jest przedział 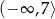 . Zatem współczynnik
. Zatem współczynnik  jest równy
jest równy
A) 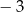 B) 4 C) 7 D) 10
B) 4 C) 7 D) 10
Zbiorem wartości funkcji kwadratowej 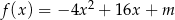 jest przedział
jest przedział 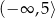 . Wtedy
. Wtedy
A) 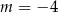 B)
B) 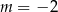 C)
C) 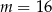 D)
D) 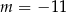
Zbiorem wartości funkcji 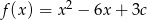 jest przedział
jest przedział 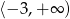 . Zatem współczynnik
. Zatem współczynnik  należy do zbioru
należy do zbioru
A) 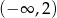 B)
B) 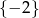 C)
C) 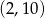 D)
D) 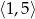
Zbiorem wartości funkcji 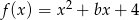 jest
jest 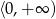 . Wynika stąd, że
. Wynika stąd, że
A) 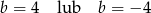 B)
B) 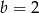 C)
C) 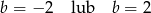 D)
D) 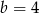
Dana jest funkcja kwadratowa 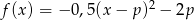 , gdzie
, gdzie 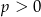 . Wówczas
. Wówczas
A) funkcja osiąga największą wartość równą 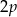 ;
;
B) funkcja ma dwa różne miejsca zerowe;
C) wierzchołek paraboli będącej wykresem 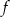 należy do prostej o równaniu
należy do prostej o równaniu 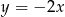 ;
;
D) dla 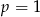 funkcja jest rosnąca w całej swojej dziedzinie.
funkcja jest rosnąca w całej swojej dziedzinie.
Jeśli funkcja kwadratowa 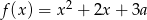 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 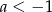 B)
B) 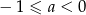 C)
C) 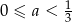 D)
D) 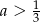
Jeśli funkcja kwadratowa 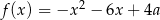 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 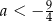 B)
B) 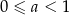 C)
C) 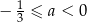 D)
D) 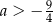
Jeśli funkcja kwadratowa 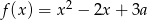 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 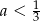 B)
B) 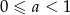 C)
C) 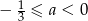 D)
D) 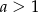
Jeśli funkcja kwadratowa 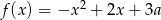 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 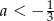 B)
B) 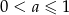 C)
C) 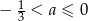 D)
D) 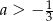
Funkcja 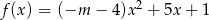 osiąga wartość największą dla
osiąga wartość największą dla
A) 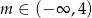 B)
B) 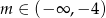 C)
C) 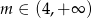 D)
D) 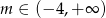
Funkcja kwadratowa 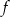 określona wzorem
określona wzorem 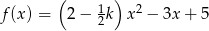 osiąga wartość największą, gdy
osiąga wartość największą, gdy
A) 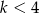 B)
B) 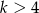 C)
C) 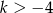 D)
D) 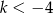
Funkcja kwadratowa 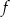 określona wzorem
określona wzorem 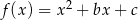 osiąga dla
osiąga dla 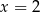 wartość najmniejszą równą 4. Wtedy
wartość najmniejszą równą 4. Wtedy
A) 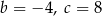 B)
B) 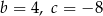
C) 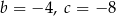 D)
D) 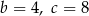
Zbiorem wartości funkcji kwadratowej 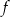 określonej wzorem
określonej wzorem 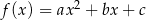 jest przedział
jest przedział 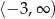 , a rozwiązaniem nierówności
, a rozwiązaniem nierówności 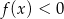 jest przedział
jest przedział 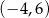 . Wskaż wzór funkcji
. Wskaż wzór funkcji 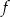 .
.
A) 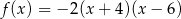 B)
B) 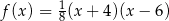
C) 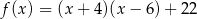 D)
D) 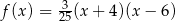
Zbiorem wartości funkcji kwadratowej 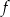 określonej wzorem
określonej wzorem 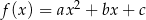 jest przedział
jest przedział 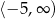 , a rozwiązaniem nierówności
, a rozwiązaniem nierówności 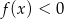 jest przedział
jest przedział 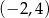 . Wskaż wzór funkcji
. Wskaż wzór funkcji 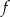 .
.
A) 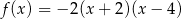 B)
B) 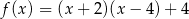
C) 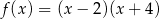 D)
D) 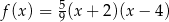
Zbiorem wartości funkcji kwadratowej 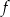 określonej wzorem
określonej wzorem 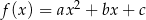 jest przedział
jest przedział 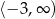 , a rozwiązaniem nierówności
, a rozwiązaniem nierówności 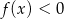 jest przedział
jest przedział 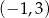 . Wskaż wzór funkcji
. Wskaż wzór funkcji 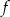 .
.
A) 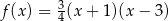 B)
B) 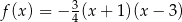
C) 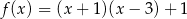 D)
D) 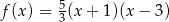
Jeśli wykres funkcji kwadratowej 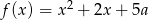 przecina prostą
przecina prostą 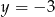 , to liczba
, to liczba  spełnia warunek
spełnia warunek
A) 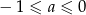 B)
B) 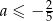 C)
C) 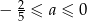 D)
D) 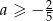
Jeżeli miejscami zerowymi funkcji kwadratowej są liczby 6 oraz -2, a wierzchołek paraboli będącej jej wykresem ma współrzędne 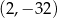 , to wzór tej funkcji można zapisać w postaci
, to wzór tej funkcji można zapisać w postaci
A) 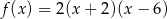 B)
B) 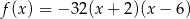
C) 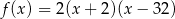 D)
D) 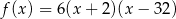
Jeżeli miejscami zerowymi funkcji kwadratowej są liczby -6 oraz 2, a wierzchołek paraboli będącej jej wykresem ma współrzędne 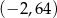 , to wzór tej funkcji można zapisać w postaci
, to wzór tej funkcji można zapisać w postaci
A) 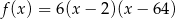 B)
B) 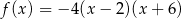
C) 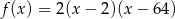 D)
D) 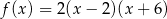
Jeżeli miejscami zerowymi funkcji kwadratowej są liczby -4 oraz 2, a wierzchołek paraboli będącej jej wykresem ma współrzędne 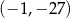 , to wzór tej funkcji można zapisać w postaci
, to wzór tej funkcji można zapisać w postaci
A) 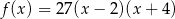 B)
B) 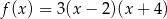
C) 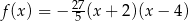 D)
D) 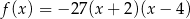
Funkcja kwadratowa 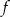 jest określona wzorem
jest określona wzorem 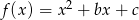 oraz
oraz 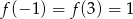 . Współczynnik
. Współczynnik 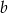 jest równy
jest równy
A) 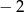 B)
B) 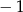 C) 0 D) 3
C) 0 D) 3
Funkcja kwadratowa 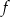 jest określona wzorem
jest określona wzorem 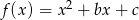 oraz
oraz 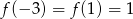 . Współczynnik
. Współczynnik 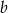 jest równy
jest równy
A) 0 B) 1 C) 2 D) 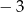
Funkcja kwadratowa 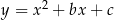 jest malejąca dla
jest malejąca dla 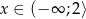 , a zbiorem jej wartości jest przedział
, a zbiorem jej wartości jest przedział 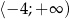 . Postać kanoniczna tej funkcji opisana jest wzorem
. Postać kanoniczna tej funkcji opisana jest wzorem
A) 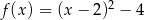 B)
B) 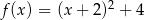
C) 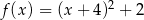 D)
D) 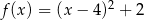
Funkcja kwadratowa 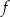 jest określona wzorem
jest określona wzorem 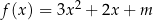 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Współczynnik
. Współczynnik 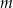 jest liczbą rzeczywistą mniejszą od zera. Funkcja
jest liczbą rzeczywistą mniejszą od zera. Funkcja 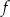
| A) ma dwa rzeczywiste miejsca zerowe, |
| B) ma jedno rzeczywiste miejsce zerowe, |
| C) nie ma rzeczywistych miejsc zerowych, |
ponieważ
1) 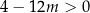 | 2) 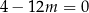 | 3) 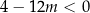 , , |
Zbiorem wartości funkcji kwadratowej 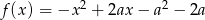 jest przedział
jest przedział 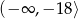 . Zatem
. Zatem
A) 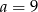 B)
B) 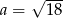 C)
C) 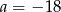 D)
D)