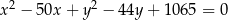Środkiem okręgu jest punkt 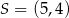 . Do okręgu należy punkt
. Do okręgu należy punkt 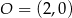 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 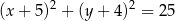 B)
B) 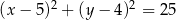
C) 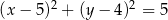 D)
D) 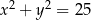
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Okrąg/Wyznacz równanie okręgu
Środkiem okręgu jest punkt 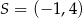 . Do okręgu należy punkt
. Do okręgu należy punkt 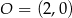 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 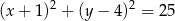 B)
B) 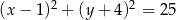
C) 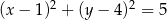 D)
D) 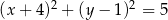
Punkt 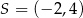 jest środkiem okręgu. Na okręgu leży punkt
jest środkiem okręgu. Na okręgu leży punkt 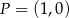 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 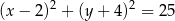 B)
B) 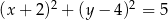
C) 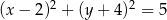 D)
D) 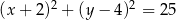
Środkiem okręgu jest punkt 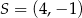 . Do okręgu należy punkt
. Do okręgu należy punkt 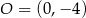 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 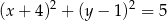 B)
B) 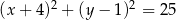
C) 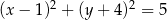 D)
D) 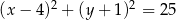
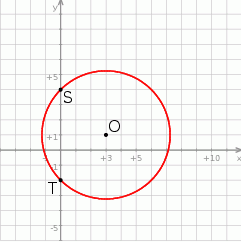
Okrąg przedstawiony na rysunku ma środek w punkcie 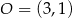 i przechodzi przez punkty
i przechodzi przez punkty 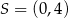 i
i 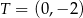 . Okrąg ten jest opisany przez równanie
. Okrąg ten jest opisany przez równanie
A) 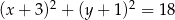 B)
B) 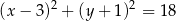
C) 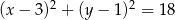 D)
D) 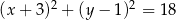
Okrąg o równaniu 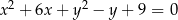 przekształcono w jednokładności o środku
przekształcono w jednokładności o środku 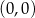 i skali
i skali 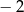 . Otrzymany okrąg ma równanie
. Otrzymany okrąg ma równanie
A) 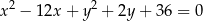 B)
B) 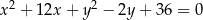
C) 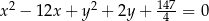 D)
D) 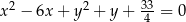
Okrąg 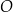 o środku
o środku 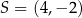 jest styczny do osi
jest styczny do osi 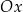 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg 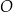 jest określony równaniem
jest określony równaniem
A) 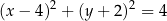 B)
B) 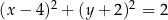
C) 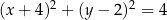 D)
D) 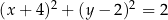
Okrąg 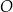 o środku
o środku 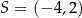 jest styczny do osi
jest styczny do osi 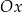 układu współrzędnych. Okrąg
układu współrzędnych. Okrąg 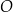 jest określony równaniem
jest określony równaniem
A) 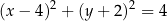 B)
B) 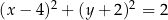
C) 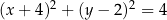 D)
D) 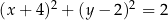
Dane są punkty 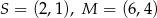 . Równanie okręgu o środku
. Równanie okręgu o środku 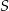 i przechodzącego przez punkt
i przechodzącego przez punkt 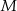 ma postać
ma postać
A) 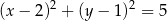 B)
B) 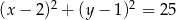
C) 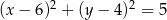 D)
D) 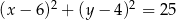
Dane są punkty 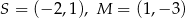 . Równanie okręgu o środku
. Równanie okręgu o środku 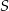 i przechodzącego przez punkt
i przechodzącego przez punkt 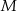 ma postać
ma postać
A) 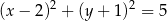 B)
B) 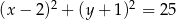
C) 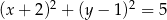 D)
D) 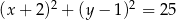
Średnicą okręgu jest odcinek 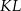 , gdzie
, gdzie 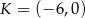 i
i 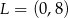 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 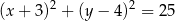 B)
B) 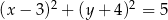
C) 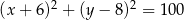 D)
D) 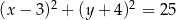
W kartezjańskim układzie współrzędnych 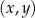 dany jest okrąg
dany jest okrąg 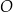 o równaniu
o równaniu
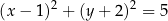
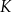 jest obrazem okręgu
jest obrazem okręgu 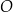 w symetrii środkowej względem początku układu współrzędnych. Okrąg
w symetrii środkowej względem początku układu współrzędnych. Okrąg 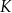 jest określony równaniem
jest określony równaniemA)
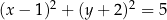 B)
B) 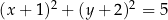
C) 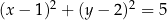 D)
D) 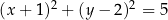
Wskaż równanie okręgu o środku 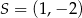 i promieniu
i promieniu 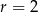 .
.
A) 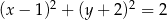 B)
B) 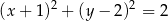
C) 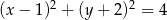 D)
D) 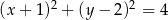
Wskaż równanie okręgu o środku w punkcie 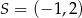 i promieniu
i promieniu 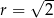 .
.
A) 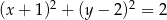 B)
B) 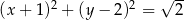
C) 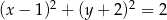 D)
D) 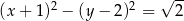
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 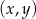 , dany jest okrąg o środku
, dany jest okrąg o środku 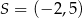 i promieniu
i promieniu 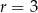 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 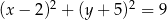 B)
B) 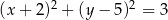
C) 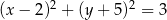 D)
D) 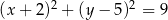
Okrąg ma środek 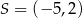 i promień
i promień 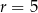 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 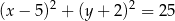 B)
B) 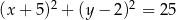
C) 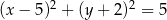 D)
D) 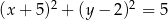
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 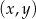 , dany jest okrąg o środku
, dany jest okrąg o środku 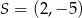 i promieniu
i promieniu 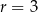 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 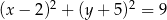 B)
B) 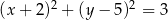
C) 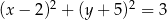 D)
D) 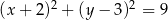
W kartezjańskim układzie współrzędnych 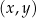 dany jest okrąg
dany jest okrąg 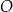 o środku
o środku 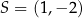 i promieniu 3. Okrąg
i promieniu 3. Okrąg 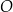 jest określony równaniem
jest określony równaniem
A) 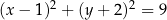 B)
B) 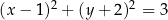
C) 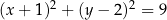 D)
D) 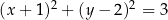
W kartezjańskim układzie współrzędnych 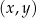 dany jest okrąg
dany jest okrąg 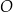 o środku
o środku 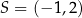 i promieniu 3. Okrąg
i promieniu 3. Okrąg 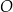 jest określony równaniem
jest określony równaniem
A) 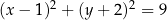 B)
B) 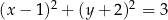
C) 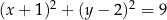 D)
D) 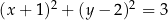
Punkt 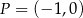 leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
leży na okręgu o promieniu 3. Równanie tego okręgu może mieć postać
A) 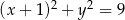 B)
B) 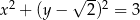
C) 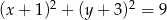 D)
D) 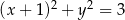
Okrąg o równaniu 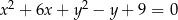 przesunięto o wektor
przesunięto o wektor ![[ 13] 9,− 2](https://img.zadania.info/zad/5991873/HzadT1x.gif) . Środek otrzymanego w ten sposób okręgu ma współrzędne
. Środek otrzymanego w ten sposób okręgu ma współrzędne
A) 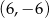 B)
B) 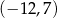 C)
C) 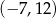 D)
D) 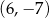
Wskaż równanie okręgu o promieniu 6.
A) 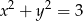 B)
B) 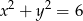 C)
C) 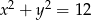 D)
D) 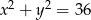
Wskaż równanie okręgu o promieniu 9.
A) 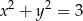 B)
B) 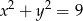 C)
C) 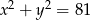 D)
D) 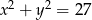
Wskaż równanie okręgu o promieniu 4.
A) 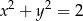 B)
B) 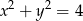 C)
C) 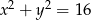 D)
D) 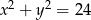
Punkt 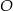 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
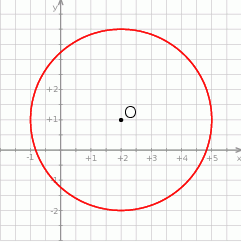
A) 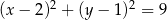 B)
B) 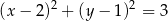
C) 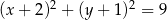 D)
D) 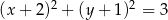
Punkt 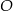 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
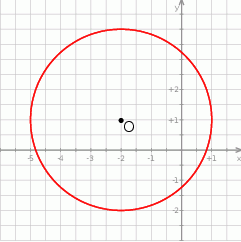
A) 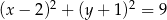 B)
B) 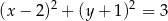
C) 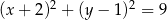 D)
D) 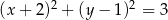
Średnicą okręgu jest odcinek 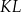 , gdzie
, gdzie 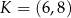 i
i 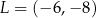 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 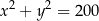 B)
B) 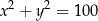 C)
C) 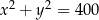 D)
D) 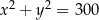
W kartezjańskim układzie współrzędnych 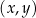 odcinek o końcach
odcinek o końcach 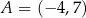 oraz
oraz 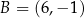 jest średnicą okręgu
jest średnicą okręgu 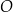 . Okrąg
. Okrąg 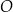 jest określony równaniem
jest określony równaniem
A) 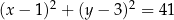 B)
B) 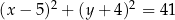
C) 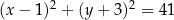 D)
D) 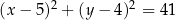
Wszystkie wierzchołki kwadratu 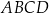 mają współrzędne nieujemne, przy czym
mają współrzędne nieujemne, przy czym 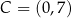 i
i 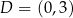 . Okrąg wpisany w kwadrat
. Okrąg wpisany w kwadrat 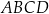 jest określony równaniem
jest określony równaniem
A) 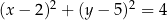 B)
B) 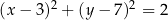
C) 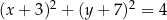 D)
D) 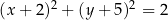
Punkty 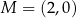 i
i 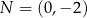 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 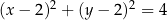 B)
B) 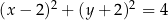
C) 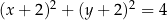 D)
D) 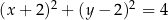
Punkty 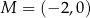 i
i 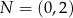 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 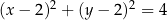 B)
B) 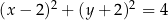
C) 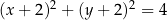 D)
D) 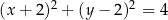
Punkt 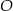 jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
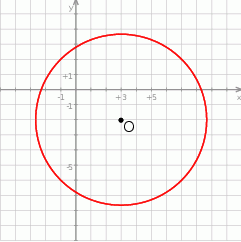
A) 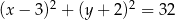 B)
B) 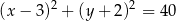
C) 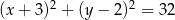 D)
D) 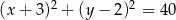
Wskaż równanie okręgu opisanego na trójkącie 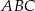 o wierzchołkach
o wierzchołkach 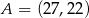 ,
, 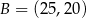 ,
, 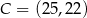
A) 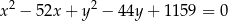 B)
B) 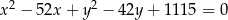
C) 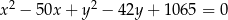 D)
D)