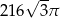Objętość stożka o wysokości 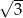 i kącie rozwarcia
i kącie rozwarcia  jest równa
jest równa
A) 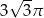 B)
B) 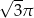 C)
C) 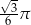 D)
D) 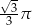
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek/Objętość
Kąt rozwarcia stożka ma miarę 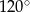 , a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
A) 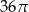 B)
B) 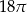 C)
C) 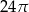 D)
D) 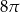
Kąt rozwarcia stożka ma miarę 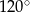 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 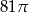 B)
B) 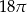 C)
C) 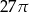 D)
D) 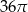
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 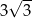 C) 3 D) 27
C) 3 D) 27
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 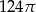 B)
B) 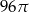 C)
C) 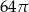 D)
D) 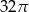
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 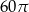 B)
B) 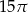 C)
C) 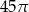 D)
D) 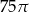
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
A) 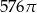 B)
B) 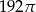 C)
C) 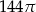 D)
D) 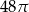
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 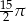 B)
B) 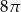 C)
C) 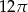 D)
D) 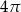
Objętość stożka o wysokości 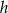 i promieniu podstawy trzy razy mniejszym od wysokości jest równa
i promieniu podstawy trzy razy mniejszym od wysokości jest równa
A) 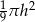 B)
B) 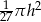 C)
C) 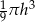 D)
D) 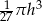
Objętość stożka o wysokości 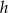 i promieniu podstawy cztery razy mniejszym od wysokości jest równa
i promieniu podstawy cztery razy mniejszym od wysokości jest równa
A) 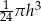 B)
B) 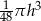 C)
C) 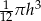 D)
D) 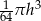
Przekrój osiowy stożka jest trójkątem rozwartokątnym o polu 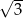 . Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
. Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
A) 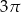 B)
B) 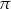 C)
C) 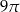 D)
D) 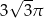
Dany jest trójkąt prostokątny o długościach boków 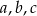 , gdzie
, gdzie 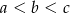 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 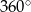 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 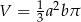 B)
B) 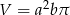 C)
C) 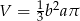 D)
D) 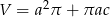
Dany jest trójkąt prostokątny o długościach boków 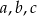 , gdzie
, gdzie 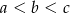 . Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt 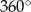 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 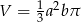 B)
B) 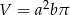 C)
C) 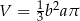 D)
D) 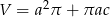
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6. Objętość tego stożka jest równa
A) 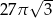 B)
B) 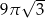 C)
C) 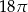 D)
D) 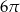
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 4. Objętość tego stożka jest równa
A) 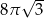 B)
B) 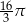 C)
C) 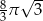 D)
D) 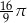
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 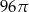 B)
B) 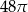 C)
C) 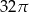 D)
D) 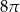
Dany jest stożek o wysokości 6 i tworzącej 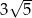 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 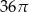 B)
B) 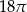 C)
C) 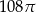 D)
D) 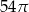
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 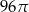 B)
B) 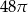 C)
C) 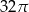 D)
D) 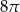
Dany jest stożek o wysokości 6 i tworzącej 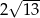 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 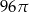 B)
B) 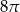 C)
C) 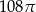 D)
D) 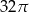
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 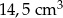 B)
B) 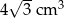 C)
C) 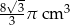 D)
D) 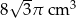
Trójkąt równoboczny o boku długości 6 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 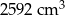 B)
B) 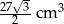 C)
C) 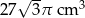 D)
D) 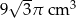
Jeżeli promień podstawy stożka zwiększymy o 20%, a wysokość zmniejszymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 15,2%
C) zwiększy się o 1,52% D) zmniejszy się o 4%
Jeżeli promień podstawy stożka zwiększymy o 10%, a wysokość zmniejszymy o 10%, to objętość stożka
A) zwiększy się o 0,89% B) nie zmieni się
C) zmniejszy się o 0,89% D) zwiększy się o 8,9%
Jeżeli promień podstawy stożka zmniejszymy o 20%, a wysokość zwiększymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 2,32%
C) zmniejszy się o 76,8% D) zmniejszy się o 23,2%
Stożki 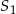 oraz
oraz 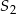 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 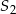 jest 4 razy dłuższy od promienia stożka
jest 4 razy dłuższy od promienia stożka 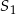 . Wobec tego objętość stożka
. Wobec tego objętość stożka 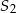 jest
jest
A) 4 razy większa od objętości stożka 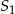
B) o 150% większa od objętości stożka 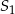
C) o 300% większa od objętości stożka 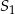
D) o 1500% większa od objętości stożka 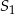
Stożki 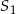 oraz
oraz 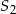 mają równe promienie podstawy. Wysokość stożka
mają równe promienie podstawy. Wysokość stożka 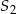 jest 4 razy dłuższa od wysokości stożka
jest 4 razy dłuższa od wysokości stożka 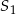 . Wobec tego objętość stożka
. Wobec tego objętość stożka 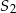 jest
jest
A) 4 razy większa od objętości stożka 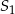
B) o 150% większa od objętości stożka 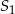
C) o 400% większa od objętości stożka 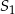
D) 0 1500% większa od objętości stożka 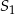
Stożki 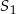 oraz
oraz 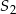 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 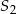 jest 2 razy dłuższy od promienia stożka
jest 2 razy dłuższy od promienia stożka 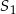 . Wobec tego objętość stożka
. Wobec tego objętość stożka 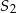 jest
jest
A) 4 razy większa od objętości stożka 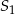
B) o 150% większa od objętości stożka 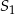
C) o 400% większa od objętości stożka 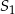
D) o 1500% większa od objętości stożka 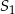
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
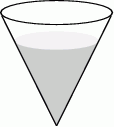
Objętość wody w naczyniu jest równa
A) 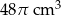 B)
B) 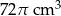 C)
C) 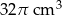 D)
D) 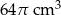
Szklane naczynie w kształcie stożka o promieniu podstawy 8 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
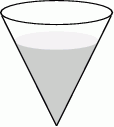
Objętość wody w naczyniu jest równa
A) 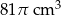 B)
B) 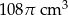 C)
C) 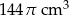 D)
D) 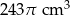
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 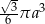 B)
B) 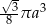 C)
C) 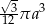 D)
D) 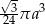
Przekrój osiowy stożka jest równoramiennym trójkątem prostokątnym o przyprostokątnej długości  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 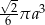 B)
B) 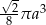 C)
C) 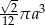 D)
D) 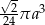
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 6. Objętość tego stożka jest równa
A) 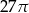 B)
B) 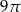 C)
C) 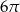 D)
D) 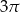
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 8. Objętość tego stożka jest równa
A) 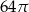 B)
B) 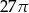 C)
C) 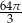 D)
D) 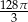
Jeśli promień podstawy stożka zwiększymy trzykrotnie, a wysokość zmniejszymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zwiększy się sześciokrotnie
Jeśli promień podstawy stożka zmniejszymy trzykrotnie, a wysokość zwiększymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zmniejszy się trzykrotnie
Jeśli promień podstawy stożka zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to objętość stożka
A) zwiększy się dwukrotnie B) nie zmieni się
C) zwiększy się czterokrotnie D) zmniejszy się czterokrotnie
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 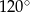 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 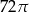 B)
B) 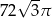 C)
C) 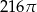 D)
D)