W trójkącie  największą miarę ma kąt przy wierzchołku
największą miarę ma kąt przy wierzchołku 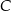 . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku 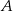 jest równa
jest równa 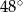 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 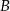 jest równa różnicy miary kąta przy wierzchołku
jest równa różnicy miary kąta przy wierzchołku 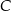 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 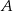 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt przy wierzchołku 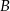 ma miarę ma miarę 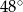 . . | P | F |
Trójkąt 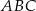 jest prostokątny. jest prostokątny. | P | F |

 najmniejszą miarę ma kąt przy wierzchołku
najmniejszą miarę ma kąt przy wierzchołku  . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku  jest równa
jest równa 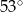 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 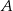 jest równa sumie miary kąta przy wierzchołku
jest równa sumie miary kąta przy wierzchołku 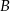 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 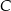 .
. 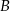 ma miarę
ma miarę 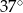 .
. jest ostrokątny.
jest ostrokątny.  ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe
ma boki długości 4 cm, 13 cm, 15 cm oraz pole równe 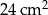 . Najdłuższa wysokość trójkąta
. Najdłuższa wysokość trójkąta 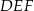 podobnego do trójkąta
podobnego do trójkąta 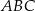 w skali 1:3 ma długość
w skali 1:3 ma długość 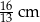
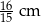
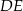 jest równoległy do podstawy
jest równoległy do podstawy 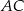 trójkąta równoramiennego
trójkąta równoramiennego 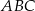 (zobacz rysunek).
(zobacz rysunek). 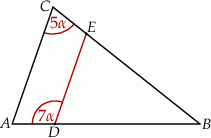
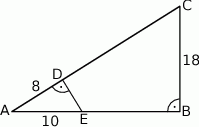
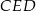 ma miarę A/B.
ma miarę A/B.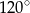
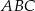 ma miarę C/D.
ma miarę C/D.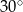
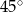
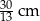
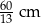
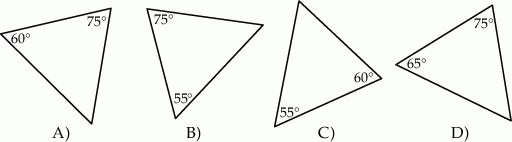
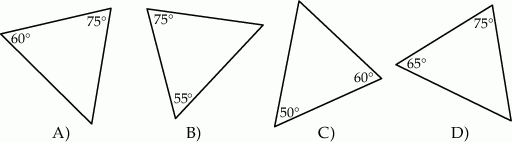
 i
i  ?
? 
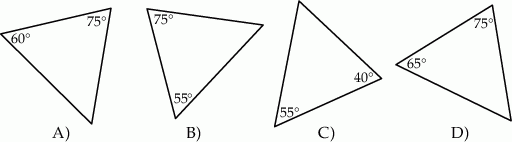
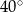 i
i 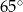 ?
? 
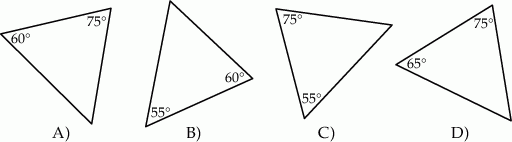
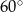 i
i 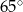 ?
? 
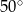 i
i 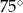 ?
? 
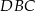 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy 
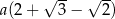
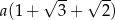
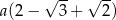
 zbudowano kwadraty. Pole kwadratu zbudowanego na boku
zbudowano kwadraty. Pole kwadratu zbudowanego na boku 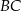 jest równe 169, a pole kwadratu zbudowanego na boku
jest równe 169, a pole kwadratu zbudowanego na boku  jest równe 25.
jest równe 25. 
 ma długość 13.
ma długość 13. 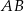 , to jego pole będzie równe 144.
, to jego pole będzie równe 144.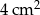 . Pole trójkąta do niego podobnego jest równe
. Pole trójkąta do niego podobnego jest równe 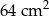 . Skala podobieństwa trójkąta większego do mniejszego jest równa
. Skala podobieństwa trójkąta większego do mniejszego jest równa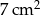 . Pole trójkąta do niego podobnego jest równe
. Pole trójkąta do niego podobnego jest równe 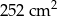 . Skala podobieństwa trójkąta mniejszego do większego jest równa
. Skala podobieństwa trójkąta mniejszego do większego jest równa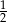
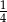
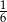
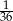
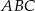 ma miarę
ma miarę 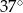 . Trójkąt
. Trójkąt 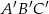 jest podobny do trójkąta
jest podobny do trójkąta 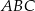 w skali 2:1. Miara najmniejszego kąta trójkąta
w skali 2:1. Miara najmniejszego kąta trójkąta 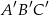 jest równa
jest równa 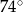
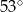
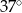
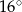
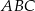 ma miarę
ma miarę 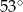 . Trójkąt
. Trójkąt 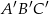 jest podobny do trójkąta
jest podobny do trójkąta 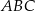 w skali 3:2. Miara najmniejszego kąta trójkąta
w skali 3:2. Miara najmniejszego kąta trójkąta 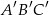 jest równa
jest równa 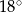
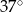
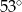
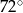
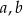 i
i  są długościami boków trójkąta oraz
są długościami boków trójkąta oraz  jest najdłuższym bokiem, to ten trójkąt jest:
jest najdłuższym bokiem, to ten trójkąt jest: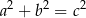
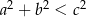
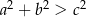 .
. 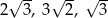
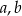 i
i  są długościami boków trójkąta oraz
są długościami boków trójkąta oraz  jest jego najdłuższym bokiem, to ten trójkąt jest:
jest jego najdłuższym bokiem, to ten trójkąt jest: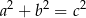
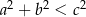
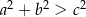 .
. 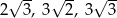
 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano sześciokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano sześciokąt (rysunek). 
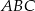 .
. 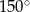 .
.  obwodu trójkąta
obwodu trójkąta 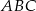 .
. 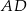 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 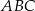 , w którym przyprostokątna
, w którym przyprostokątna  ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry  ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek). 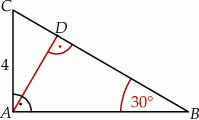
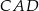 ma miarę A/B.
ma miarę A/B.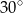
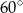
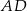 ma długość C/D.
ma długość C/D.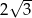
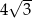
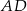 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 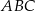 , w którym przeciwprostokątna
, w którym przeciwprostokątna  ma długość 4 cm i kąt ostry
ma długość 4 cm i kąt ostry  ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek). 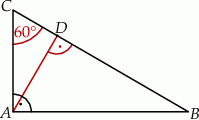
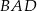 ma miarę A/B.
ma miarę A/B.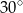
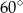
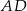 ma długość C/D.
ma długość C/D.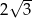
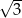
 o przyprostokątnych długości 15 cm i 20 cm. Przeciwprostokątna trójkąta
o przyprostokątnych długości 15 cm i 20 cm. Przeciwprostokątna trójkąta  podobnego do trójkąta
podobnego do trójkąta 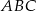 w skali 2:1 ma długość
w skali 2:1 ma długość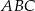 o przyprostokątnych długości 30 cm i 40 cm. Przeciwprostokątna trójkąta
o przyprostokątnych długości 30 cm i 40 cm. Przeciwprostokątna trójkąta 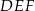 podobnego do trójkąta
podobnego do trójkąta 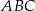 w skali 1:2 ma długość
w skali 1:2 ma długość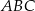 o podstawie długości 10 cm i polu
o podstawie długości 10 cm i polu 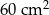 . Ramię trójkąta
. Ramię trójkąta 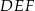 podobnego do trójkąta
podobnego do trójkąta 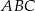 w skali 4:1 ma długość
w skali 4:1 ma długość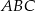 .
.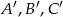 .
. jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 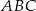
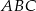 jest dwa ray mniejszy od obwodu trójkąta
jest dwa ray mniejszy od obwodu trójkąta 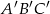
 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa 
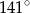
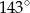
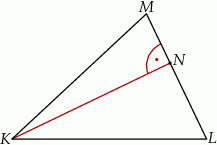
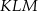 poprowadzono wysokość
poprowadzono wysokość 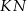 . Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych:
. Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych: 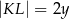 ,
, 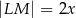 ,
, 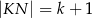 .
. 
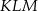 opisano wyrażeniem
opisano wyrażeniem 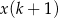
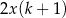
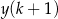
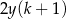
 i
i 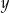 . Bok tego rombu ma długość
. Bok tego rombu ma długość 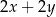
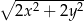
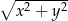
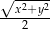
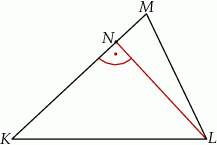
 poprowadzono wysokość
poprowadzono wysokość 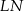 . Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych:
. Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych: 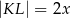 ,
, 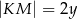 ,
, 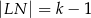 .
. 
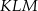 opisano wyrażeniem
opisano wyrażeniem 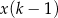
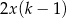
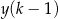
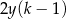
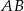 i
i 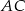 trójkąta prostokątnego
trójkąta prostokątnego 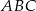 wybrano punkty
wybrano punkty 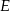 i
i 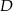 tak, że
tak, że 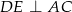 ,
, 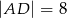 i
i 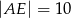 . Przyprostokątna
. Przyprostokątna 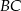 trójkąta
trójkąta 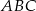 ma długość 18.
ma długość 18.