W trójkącie równoramiennym 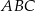 , w którym
, w którym 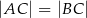 i
i 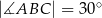 poprowadzono wysokość
poprowadzono wysokość 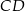 i dwusieczną kąta
i dwusieczną kąta 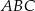 przecinającą bok
przecinającą bok 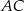 w punkcie
w punkcie 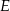 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 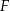 .
.
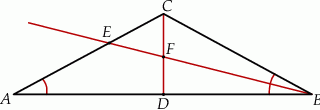
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
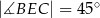 | P | F |
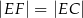 | P | F |

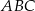 , w którym
, w którym 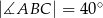 ,
, 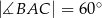 poprowadzono dwusieczne
poprowadzono dwusieczne 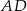 i
i 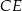 , które przecinają się w punkcie
, które przecinają się w punkcie 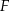 .
. 
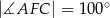
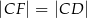
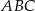 , w którym
, w którym 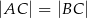 i
i 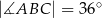 poprowadzono wysokość
poprowadzono wysokość 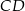 i dwusieczną kąta
i dwusieczną kąta 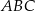 przecinającą bok
przecinającą bok 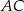 w punkcie
w punkcie 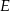 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 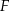 .
. 
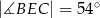
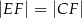
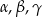 pewnego trójkąta spełniają dwa warunki:
pewnego trójkąta spełniają dwa warunki: 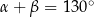 i
i 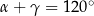 .
.  ma miarę
ma miarę 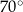 .
. 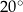 .
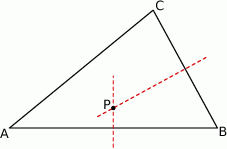
. 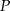 jest punktem wspólnym symetralnych boków
jest punktem wspólnym symetralnych boków 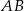 i
i 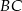 trójkąta
trójkąta 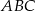 .
. 
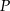 od wierzchołków
od wierzchołków 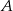 i
i 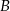 jest taka sama.
jest taka sama.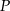 od wierzchołków
od wierzchołków 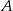 i
i 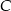 jest taka sama.
jest taka sama.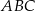 narysowano dwie wysokości:
narysowano dwie wysokości: 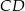 i
i 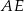 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 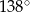 .
. 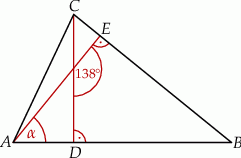
 zaznaczony na rysunku?
zaznaczony na rysunku? 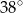
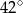
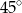
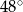
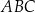 narysowano dwie wysokości:
narysowano dwie wysokości: 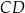 i
i 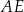 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 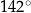 .
. 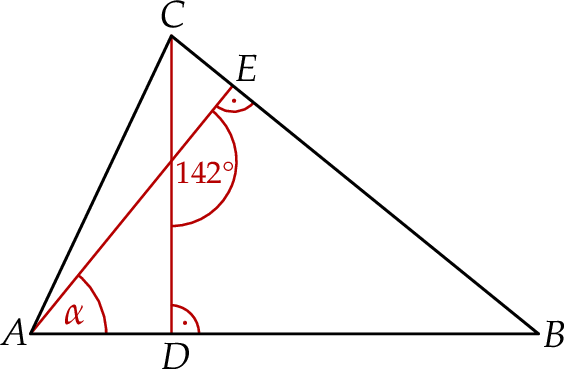
 zaznaczony na rysunku?
zaznaczony na rysunku? 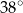
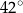
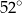
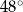
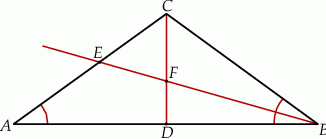
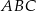 , w którym kąt
, w którym kąt 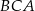 ma miarę
ma miarę 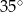 . Punkt
. Punkt 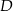 leży na boku
leży na boku 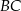 tego trójkąta. Odcinek
tego trójkąta. Odcinek 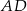 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 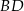 . Kąt
. Kąt 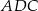 ma miarę
ma miarę 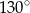 (zobacz rysunek poniżej).
(zobacz rysunek poniżej). 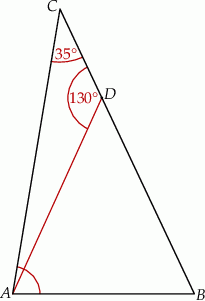
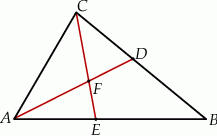
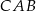 ma miarę
ma miarę 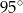
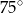
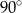
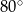
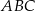 , w którym kąt
, w którym kąt 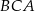 ma miarę
ma miarę 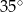 . Punkt
. Punkt 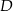 leży na boku
leży na boku 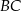 tego trójkąta. Odcinek
tego trójkąta. Odcinek 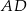 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 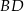 . Kąt
. Kąt 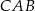 ma miarę
ma miarę 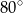 (zobacz rysunek poniżej).
(zobacz rysunek poniżej). 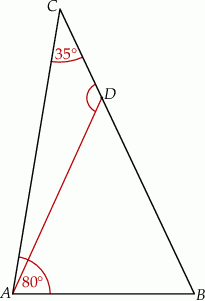
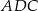 ma miarę
ma miarę 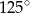
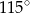
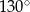
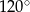
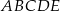
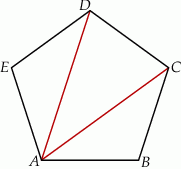
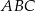 i
i 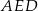 są przystające.
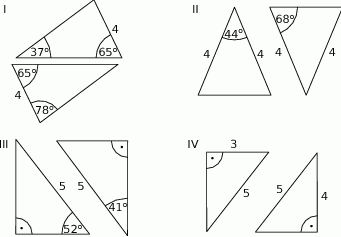
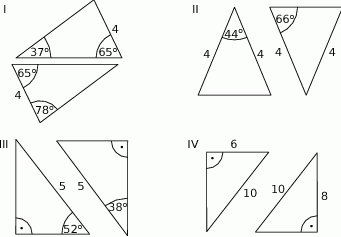
są przystające. 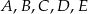 , które są przystające do trójkąta
, które są przystające do trójkąta  .
. 
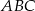 jest prostokątny, ale nie jest równoramienny. Odcinek
jest prostokątny, ale nie jest równoramienny. Odcinek 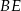 jest wysokością w trójkącie
jest wysokością w trójkącie 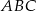 , a półprosta
, a półprosta 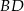 jest dwusieczną kąta prostego.
jest dwusieczną kąta prostego. 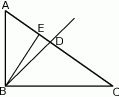
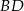 jest dwusieczną kąta
jest dwusieczną kąta 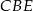 .
. 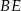 jest wysokością w trójkącie
jest wysokością w trójkącie 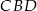 .
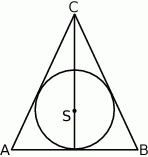
.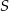 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 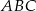 (
(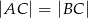 ).
). 
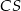 zawiera środkową trójkąta
zawiera środkową trójkąta 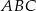 .
.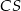 jest symetralną odcinka
jest symetralną odcinka 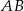
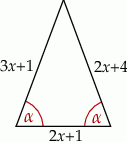
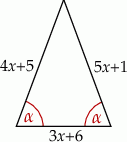
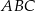 o podstawie
o podstawie 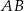 narysowano wysokość
narysowano wysokość 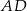 , jak na rysunku. Kąt między tą wysokością a podstawą
, jak na rysunku. Kąt między tą wysokością a podstawą 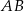 jest równy
jest równy 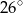 .
. 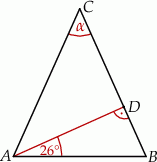
 zaznaczony na rysunku?
zaznaczony na rysunku? 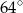
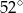
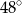
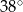
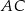 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa 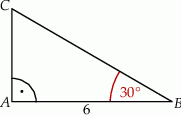
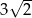
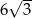
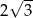
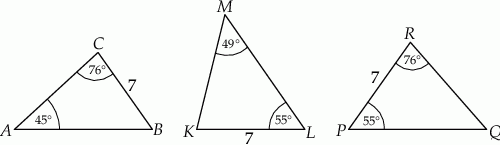
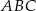 jest przystający do trójkąta
jest przystający do trójkąta 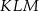 .
. 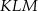 jest przystający do trójkąta
jest przystający do trójkąta 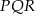 .
. 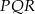 jest przystający do trójkąta
jest przystający do trójkąta 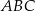 .
. 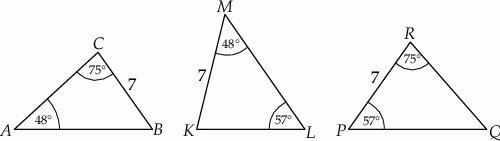
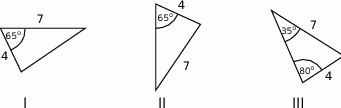
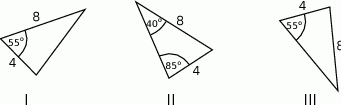
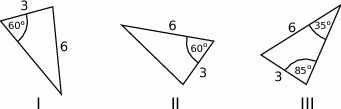
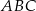 jest przystający do trójkąta
jest przystający do trójkąta 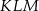 .
. 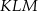 jest przystający do trójkąta
jest przystający do trójkąta 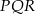 .
. 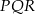 jest przystający do trójkąta
jest przystający do trójkąta 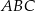 .
. 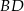 i
i 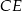 trójkąta równobocznego
trójkąta równobocznego 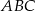 przecinają się w punkcie
przecinają się w punkcie 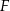 .
. 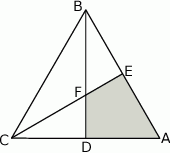
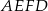 stanowi
stanowi  pola trójkąta
pola trójkąta 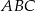 .
.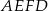 ma miarę
ma miarę 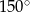 .
. 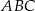 zaznaczono punkty
zaznaczono punkty 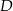 i
i 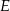 . Odcinek
. Odcinek 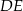 podzielił trójkąt
podzielił trójkąt 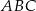 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 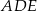 i czworokąt
i czworokąt 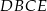 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 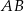 ma długość
ma długość 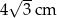 , a odcinek
, a odcinek 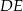 ma długość 3 cm.
ma długość 3 cm. 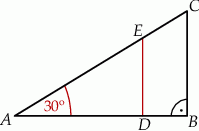
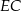 jest równa
jest równa 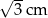
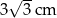
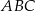 zaznaczono punkty
zaznaczono punkty 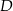 i
i 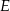 . Odcinek
. Odcinek 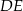 podzielił trójkąt
podzielił trójkąt 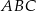 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 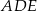 i czworokąt
i czworokąt 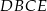 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 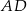 ma długość
ma długość 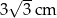 , a odcinek
, a odcinek 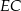 ma długość 2 cm.
ma długość 2 cm. 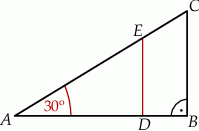
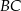 jest równa
jest równa 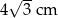
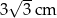
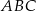 o obwodzie 34 cm poprowadzono odcinek
o obwodzie 34 cm poprowadzono odcinek 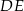 . Obwód trójkąta
. Obwód trójkąta 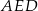 jest równy 16 cm, a obwód czworokąta
jest równy 16 cm, a obwód czworokąta 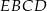 – 30 cm.
– 30 cm. 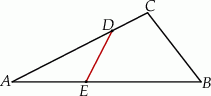
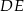 jest równa
jest równa 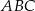 o obwodzie 128 cm poprowadzono odcinek
o obwodzie 128 cm poprowadzono odcinek 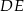 . Obwód trójkąta
. Obwód trójkąta 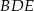 jest równy 84 cm, a obwód czworokąta
jest równy 84 cm, a obwód czworokąta 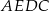 – 100 cm.
– 100 cm. 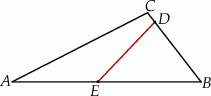
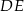 jest równa
jest równa 