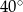Od kartonika w kształcie trójkąta równobocznego odcięto naroża, tak jak pokazano na rysunku i otrzymano sześciokąt foremny o bokach długości 3.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był trójkątem o obwodzie 27. | P | F |
| Suma pól odciętych naroży jest dwa razy mniejsza od pola sześciokąta. | P | F |

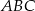 spełnione są warunki:
spełnione są warunki: 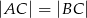 ,
, 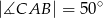 . Odcinek
. Odcinek 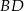 jest dwusieczną kąta
jest dwusieczną kąta 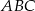 , a odcinek
, a odcinek 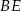 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 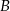 na bok
na bok 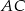 . Miara kąta
. Miara kąta 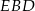 jest równa
jest równa 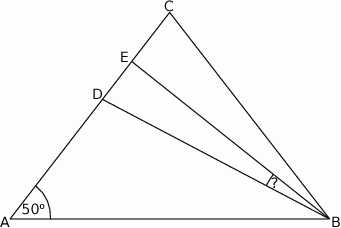
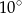
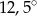
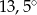
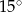
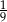
 , drugi ma miarę o
, drugi ma miarę o 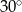 większą niż kąt
większą niż kąt  , a trzeci ma miarę trzy razy większą niż kąt
, a trzeci ma miarę trzy razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest  , drugi ma miarę o
, drugi ma miarę o 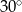 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest  , drugi ma miarę o
, drugi ma miarę o 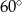 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  .
. 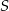 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 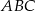 , a punkty
, a punkty 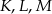 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 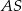 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 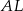 ma długość 24 cm.
ma długość 24 cm. 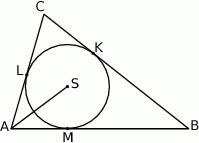
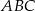 jest równy 9 cm.
jest równy 9 cm.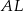 i
i 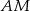 mają tę samą długość.
mają tę samą długość. 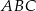 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy 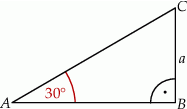
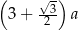
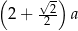
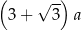
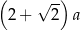
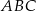 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy 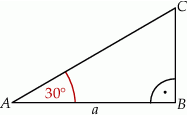
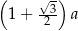
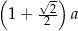
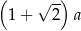
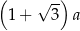
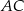 trójkąt równobocznego
trójkąt równobocznego 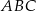 o polu równym
o polu równym 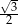 zbudowano równoramienny trójkąt prostokątny
zbudowano równoramienny trójkąt prostokątny  .
. 
 jest równe
jest równe 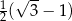 .
.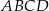 jest równy
jest równy 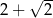 .
.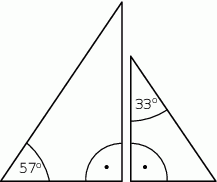
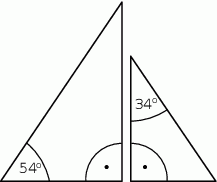
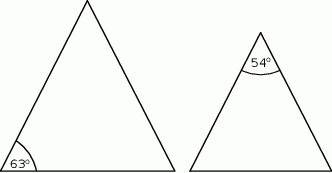

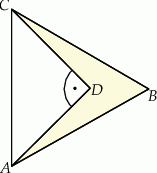
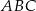 poprowadzono wysokości
poprowadzono wysokości 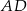 i
i 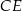 . Odcinek
. Odcinek 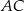 ma taką samą długość
ma taką samą długość 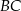 , a kąt
, a kąt 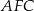 ma miarę
ma miarę 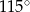 (zobacz rysunek).
(zobacz rysunek). 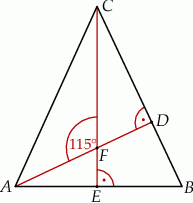
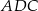 jest równoramienny.
jest równoramienny.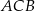 ma miarę
ma miarę 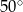 .
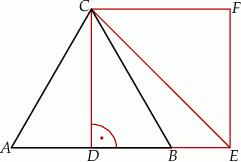
. 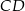 trójkąta równobocznego
trójkąta równobocznego 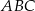 o boku długości 4 zbudowano kwadrat
o boku długości 4 zbudowano kwadrat 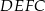 .
. 
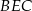 jest równe
jest równe 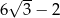
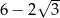
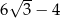
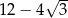
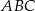 o boku długości 10 cm. W tym trójkącie poprowadzono wysokość
o boku długości 10 cm. W tym trójkącie poprowadzono wysokość 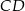 . Obwód trójkąta
. Obwód trójkąta 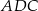 jest równy
jest równy 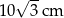
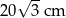
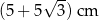
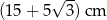
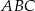 o boku długości 8 cm. W tym trójkącie poprowadzono wysokość
o boku długości 8 cm. W tym trójkącie poprowadzono wysokość 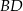 . Obwód trójkąta
. Obwód trójkąta 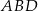 jest równy
jest równy 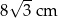
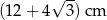
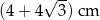
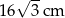
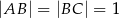 oraz
oraz 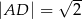 .
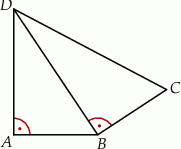
. 
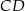 jest równa
jest równa 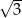
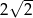
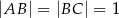 oraz
oraz 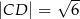 .
. 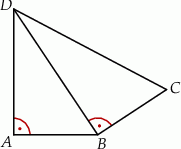
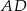 jest równa
jest równa 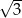
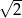
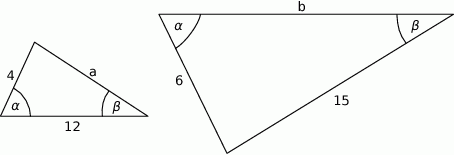
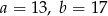
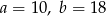
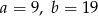
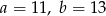
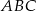 i
i 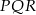 są podobne. Bok
są podobne. Bok 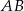 trójkąta
trójkąta 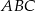 ma długość
ma długość 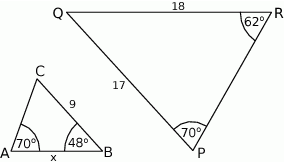
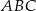 i
i 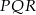 są podobne. Bok
są podobne. Bok 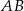 trójkąta
trójkąta 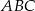 ma długość
ma długość 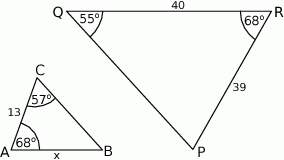
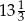
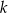 i
i 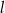 przecięto prostymi
przecięto prostymi 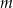 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku. 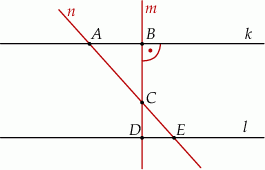
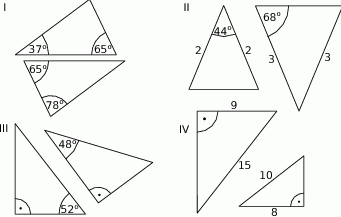
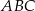 i
i 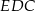 są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C.
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C. 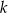 i
i 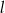 przecięto prostymi
przecięto prostymi 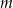 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku. 
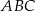 i
i 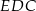 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D. 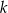 i
i 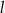 przecięto prostymi
przecięto prostymi 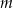 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku. 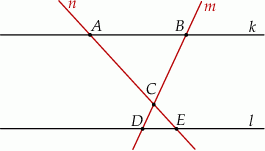
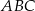 i
i 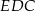 są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
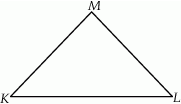
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D. 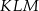 o ramionach
o ramionach 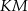 i
i 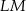 . Miara kąta
. Miara kąta 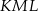 jest dwa razy większa niż miara kąta
jest dwa razy większa niż miara kąta 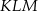 .
. 
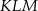 jest równa A/B.
jest równa A/B.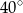
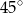
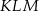 jest C/D.
jest C/D.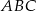 .
.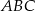 , przechodzącą przez punkt
, przechodzącą przez punkt 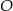 . Punkt przecięcia prostej prostopadłej i tego boku oznaczyć literą
. Punkt przecięcia prostej prostopadłej i tego boku oznaczyć literą 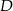 ,
, 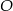 i promieniu
i promieniu 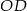 ,
, 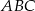 i ich punkt przecięcia oznaczyć literą
i ich punkt przecięcia oznaczyć literą 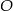 .
.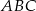 . 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą
. 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą 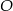 .
.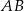 i przechodzącą przez punkt
i przechodzącą przez punkt 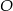 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 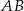 oznaczono literą
oznaczono literą 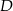 .
.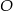 i promieniu
i promieniu 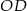 .
.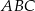 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 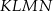 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy 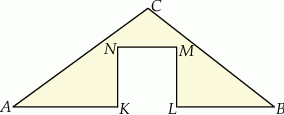
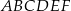 wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
wpisano trójkąt równoboczny tak jak przedstawiono na rysunku. 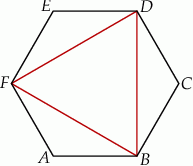
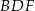 jest większy niż 80% obwodu sześciokąta
jest większy niż 80% obwodu sześciokąta 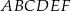 .
.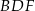 jest 3 razy większe od pola trójkąta
jest 3 razy większe od pola trójkąta 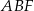 .
. 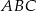 mają miary
mają miary 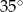 i
i 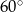 . Trójkąt podobny do trójkąta
. Trójkąt podobny do trójkąta 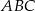 może mieć kąty o miarach
może mieć kąty o miarach 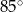 i
i 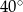
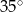 i
i 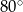
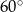 i
i 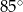
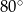 i
i