Dany jest trójkąt prostokątny o polu 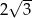 i kącie ostrym
i kącie ostrym 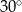 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Oblicz długość...
Dany jest trójkąt prostokątny o polu 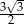 i kącie ostrym
i kącie ostrym 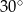 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 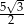 i kącie ostrym
i kącie ostrym  . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny 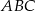 , w którym przyprostokątna
, w którym przyprostokątna 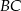 ma długość 6. Punkt
ma długość 6. Punkt 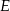 jest środkiem przeciwprostokątnej
jest środkiem przeciwprostokątnej 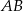 , spodek
, spodek 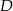 wysokości
wysokości 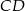 leży między punktami
leży między punktami 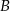 i
i 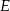 , a odległość między punktami
, a odległość między punktami 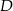 i
i 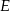 jest równa 7 (zobacz rysunek).
jest równa 7 (zobacz rysunek).
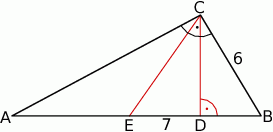
Oblicz obwód trójkąta 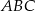 .
.
W trójkącie prostokątnym równoramiennym 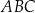 o przeciwprostokątnej
o przeciwprostokątnej 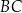 punkt
punkt 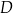 jest środkiem ramienia
jest środkiem ramienia 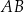 . Odcinek
. Odcinek 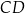 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek).
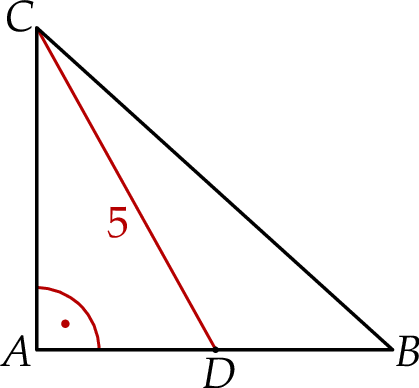
Oblicz obwód trójkąta 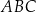 .
.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70, a pole 210.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 40, a pole 60.
Jeden z kątów trójkąta prostokątnego ma miarę 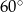 , promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
, promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Promień okręgu opisanego na trójkącie prostokątnym ma długość 3 dm, a długość promienia okręgu wpisanego w trójkąt prostokątny wynosi 1 dm. Oblicz obwód tego trójkąta.
Przekątne trapezu 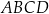 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie 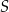 . Podstawa
. Podstawa 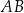 tego trapezu ma długość 15, a odcinki
tego trapezu ma długość 15, a odcinki 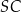 i
i 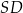 mają odpowiednio długości 6 i 8. Oblicz pole trójkąta
mają odpowiednio długości 6 i 8. Oblicz pole trójkąta 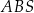 .
.
Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Przeciwprostokątna trójkąta prostokątnego ma długość 34 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Na okręgu o promieniu 2 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.
Na okręgu o promieniu 3 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.
Trójkąty prostokątne 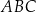 i
i 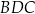 spełniają warunki:
spełniają warunki: 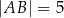 ,
, 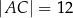 ,
, 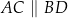 oraz
oraz 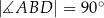 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość odcinka 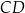 .
.
W trójkącie prostokątnym 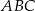 przyprostokątne mają długości:
przyprostokątne mają długości: 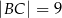 ,
, 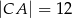 . Na boku
. Na boku 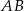 wybrano punkt
wybrano punkt 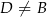 tak, że odcinki
tak, że odcinki 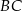 i
i 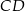 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 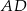 .
.
Pole prostokąta 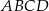 jest równe 60, a promień okręgu wpisanego w trójkąt
jest równe 60, a promień okręgu wpisanego w trójkąt 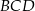 jest równy 2. Oblicz obwód tego prostokąta.
jest równy 2. Oblicz obwód tego prostokąta.
W trójkącie prostokątnym 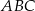 (
(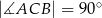 ,
, 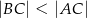 ) poprowadzono prostą przechodzącą przez wierzchołek
) poprowadzono prostą przechodzącą przez wierzchołek 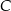 trójkąta która przecina przeciwprostokątną w punkcie
trójkąta która przecina przeciwprostokątną w punkcie 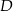 , takim, że
, takim, że 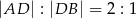 . Oblicz długość przeciwprostokątnej jeśli
. Oblicz długość przeciwprostokątnej jeśli 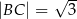 i
i 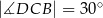 .
.
Stosunek długości przyprostokątnych trójkąta prostokątnego wynosi 3:8, a środkowa poprowadzona do dłuższej przyprostokątnej ma długość 15.
- Oblicz długość przyprostokątnych trójkąta.
- Oblicz odległość środka ciężkości trójkąta od dłuższej przyprostokątnej.
Jeden kąt ostry trójkąta prostokątnego ma miarę  . Wyznacz długości boków tego trójkąta wiedząc, że wysokość poprowadzona z wierzchołka kąta prostego ma długość
. Wyznacz długości boków tego trójkąta wiedząc, że wysokość poprowadzona z wierzchołka kąta prostego ma długość 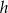 .
.
W trójkącie prostokątnym 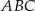 jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta
jedna z przyprostokątnych jest o 7 dłuższa od drugiej, a promień okręgu wpisanego w ten trójkąt jest równy 3. Oblicz obwód trójkąta 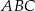 .
.
Wysokość poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego dzieli przeciwprostokątna na odcinki o długościach 1 i 2. Oblicz długości boków tego trójkąta.
W trójkącie prostokątnym 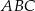 przyprostokątne mają długości:
przyprostokątne mają długości: 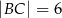 ,
, 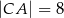 . Na boku
. Na boku 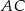 wybrano punkt
wybrano punkt 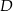 tak, że odcinki
tak, że odcinki 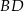 i
i 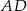 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 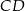 .
.
Trójkąty prostokątne 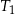 i
i 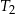 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 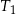 mają długości 5 i 12. Przeciwprostokątna trójkąta
mają długości 5 i 12. Przeciwprostokątna trójkąta 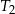 ma długość 26. Oblicz pole trójkąta
ma długość 26. Oblicz pole trójkąta 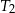 .
.
Trójkąty prostokątne 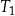 i
i 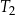 są podobne. Przyprostokątne trójkąta
są podobne. Przyprostokątne trójkąta 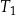 mają długości 7 i 24. Przeciwprostokątna trójkąta
mają długości 7 i 24. Przeciwprostokątna trójkąta 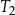 ma długość 50. Oblicz pole trójkąta
ma długość 50. Oblicz pole trójkąta 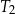 .
.

