Wyznacz wszystkie liczby rzeczywiste 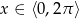 , dla których
, dla których
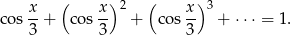
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby rzeczywiste 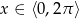 , dla których
, dla których
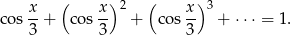
Rozwiąż równanie 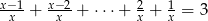 .
.
Rozwiąż równanie 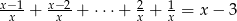 .
.
Rozwiąż równanie 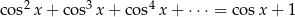
Wyznacz wszystkie liczby rzeczywiste 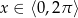 , które spełniają równanie
, które spełniają równanie
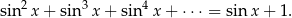
Wyznacz te wartości parametru  , dla których równanie
, dla których równanie
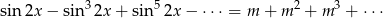
ma rozwiązania?
Dany jest nieskończony szereg geometryczny
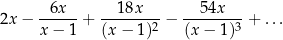
Wyznacz wszystkie wartości zmiennej  (różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa
(różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest równa 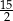 .
.
Dany jest nieskończony szereg geometryczny
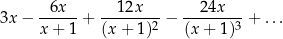
Wyznacz wszystkie wartości zmiennej  (różnej od
(różnej od 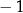 i od 0), dla których suma tego szeregu istnieje i jest równa
i od 0), dla których suma tego szeregu istnieje i jest równa 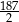 .
.
Rozwiąż równanie 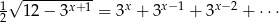 .
.
Rozwiąż równanie
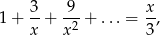
gdzie lewa strona jest sumą kolejnych wyrazów ciągu geometrycznego.
Zbadaj liczbę pierwiastków równania 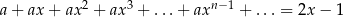 w zależności od wartości parametru
w zależności od wartości parametru  .
.
Rozwiąż równanie
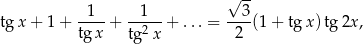
w którym lewa strona jest sumą wyrazów nieskończonego ciągu geometrycznego.
Rozwiąż równanie 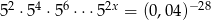 .
.
Rozwiąż równanie 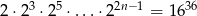 , gdy
, gdy 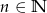 .
.
Dla jakich wartości parametru  równanie
równanie 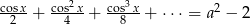 , ma rozwiązanie?
, ma rozwiązanie?
Znajdź największą liczbę naturalną 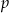 , dla której ciąg
, dla której ciąg 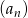 , określony wzorem
, określony wzorem 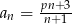 jest malejący. Dla znalezionej wartości
jest malejący. Dla znalezionej wartości 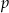 rozwiąż równanie
rozwiąż równanie
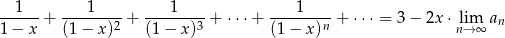
Dla jakich wartości parametru 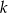 równanie
równanie 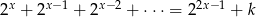 ma dokładnie jedno rozwiązanie?
ma dokładnie jedno rozwiązanie?
O funkcji 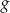 wiadomo, że
wiadomo, że 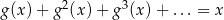 , gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru
, gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru 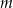 równanie
równanie 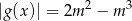 posiada dwa rozwiązania?
posiada dwa rozwiązania?
Rozwiąż równanie 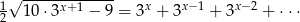 .
.
Dana jest funkcja
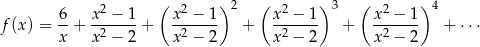
Wyznacz dziedzinę i miejsca zerowe funkcji 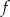 .
.
Rozwiąż równanie:
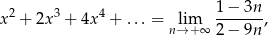
gdzie lewa strona równania jest sumą nieskończonego ciągu geometrycznego.
Rozwiąż równanie 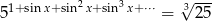 .
.
Dany jest nieskończony ciąg geometryczny
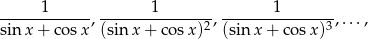
gdzie 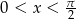 .
.
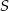 wszystkich wyrazów tego ciągu.
wszystkich wyrazów tego ciągu.  wszystkich wyrazów tego ciągu wynosi
wszystkich wyrazów tego ciągu wynosi 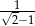 , oblicz
, oblicz  .
.Rozwiąż równanie 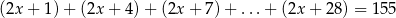 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
Rozwiąż równanie 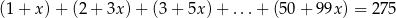 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
Rozwiąż równanie 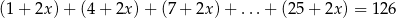 , jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
, jeśli wiadomo, że składniki po lewej stronie są kolejnymi wyrazami pewnego ciągu arytmetycznego.
