W pudełku są 24 kule, z czego 15 białych i 9 czarnych. Do tego pudełka dołożono pewną liczbę kul białych i trzy razy większą liczbę kul czarnych, a następnie wylosowano jedną kulę z pudełka. Prawdopodobieństwo, że wylosowana kula jest biała jest równe 0,34. Ile kul czarnych dołożono do pudełka?
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Szuflady, pudełka
Rozmieszczamy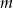 
różnych listów w 
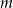rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że:
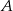– co najmniej jedna skrytka jest pusta? 
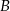– co najmniej dwie skrytki są puste?
W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że w wyniku losowania otrzymamy dwa cukierki czekoladowe?
Ukryj
Podobne zadania
W dwóch pudełkach są cukierki. W pierwszym pudełku jest 15 cukierków czekoladowych i 5 owocowych, a w drugim pudełku jest 20 cukierków czekoladowych i 30 cukierków owocowych. Losujemy cukierek najpierw z pierwszego, a potem z drugiego pudełka. Jakie jest prawdopodobieństwo, że jeden z wylosowanych cukierków będzie czekoladowy, a drugi owocowy?
Rozmieszczamy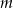 
różnych listów w 
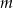rozróżnialnych, ponumerowanych skrytkach. Jakie jest prawdopodobieństwo takiego rozmieszczenia, że dwa ustalone listy znalazły się w różnych skrytkach?
Danych jest 5 pudełek ponumerowanych liczbami od 1 do 5. W każdym pudełku znajduje się 20 kul ponumerowanych liczbami od 1 do 20. Z każdego pudełka wybieramy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że każda z wylosowanych liczb jest mniejsza od wszystkich liczb wylosowanych z pudełek o większych numerach. Wynik podaj w postaci ułamka nieskracalnego.
Do 12 ponumerowanych szuflad wkładamy losowo 13 pojedynczych skarpetek, przy czym dokładnie dwie z nich tworzą parę. Jakie jest prawdopodobieństwo otrzymania konfiguracji, w której żadna szuflada nie jest pusta oraz skarpetki tworzące parę znajdują się w różnych szufladach.
10 kul rozmieszczamy w 10 szufladach. Jakie jest prawdopodobieństwo tego, że każda szuflada będzie zajęta?
W jednej szufladzie znajdują się 3 szaliki czarne i 4 szaliki niebieskie, a w drugiej szufladzie są 2 czapki czarne i 1 niebieska. Wyjmujemy losowo jeden szalik i jedną czapkę. Które prawdopodobieństwo jest większe: zdarzenia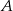 
, że otrzymamy komplet w jednym kolorze, czy zdarzenia 
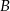, że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:
- wylosujemy dwa klocki białe;
- wylosujemy klocki tego samego koloru.
W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe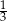 
i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
Pięć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Ukryj
Podobne zadania
Sześć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobieństwo, że przynajmniej dwa listy znajdą się w tej samej skrzynce?
Na stole stoją dwa identyczne koszyki, w których znajduje się po 15 jednakowej wielkości piłeczek. Piłeczki są w kolorze żółtym i czerwonym. W obu koszykach liczba piłeczek żółtych jest taka sama. Z każdego koszyka losujemy jedną piłeczkę. Ile powinno być w każdym koszyku żółtych piłeczek, aby prawdopodobieństwo wylosowania piłeczek różnych kolorów było największe?
W pojemniku umieszczono 50 drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie 15 czerwonych sześcianów, 18 klocków niebieskich i 31 klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą.
W pojemniku znajduje się 28 kul, przy czym 
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby 
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
W jednej szufladzie znajduje się 6 czapek: 3 zielone, 2 czerwone i 1 niebieska, a w drugiej szufladzie jest 7 szalików: 2 zielone, 1 czerwony i 4 niebieskie. Wyjęto losowo jedną czapkę i jeden szalik. Oblicz prawdopodobieństwo zdarzenia A – wylosowana czapka i wylosowany szalik są tego samego koloru.
Ukryj
Podobne zadania
W kuchni stoją dwa koszyki. W pierwszym jest 9 papryk: 1 zielona, 4 czerwone i 4 żółte. W drugim 12 papryk: 4 zielone, 3 czerwone i 5 żółtych. Kucharz wyjmuje losowo po jednej papryce z każdego koszyka. Oblicz prawdopodobieństwo, że obie papryki będą tego samego koloru.
W pojemniku znajdują się dwie kule białe i trzy czerwone. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
Ukryj
Podobne zadania
W pojemniku znajdują się dwie kule czerwone i trzy białe. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
Danych jest osiem kul z numerami od 1 do 8, oraz dziesięć szuflad z numerami od 1 do 10. Rozmieszczamy w dowolny sposób kule w szufladach. Oblicz prawdopodobieństwa następujących zdarzeń:
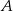– wszystkie kule znajdą się w szufladach z numerami parzystymi. 
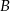– dokładnie dwie szuflady pozostaną puste.
W pudełku znajduje się 8 piłeczek oznaczonych kolejnymi liczbami naturalnymi od 1 do 8. Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez 4. Wynik podaj w postaci ułamka zwykłego.
Listonosz losowo rozmieszcza 7 listów w 5 różnych skrzynkach na listy. Oblicz prawdopodobieństwo, że w każdej skrzynce znajdzie się przynajmniej jeden list.
