Punkty 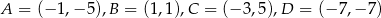 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Trapez
Punkty 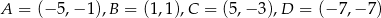 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Punkty o współrzędnych 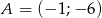 ,
, 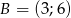 ,
, 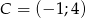 są wierzchołkami trapezu. Ramię trapezu
są wierzchołkami trapezu. Ramię trapezu 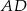 jest prostopadłe do podstaw
jest prostopadłe do podstaw 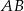 i
i 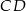 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 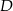 oraz pole powierzchni tego trapezu.
oraz pole powierzchni tego trapezu.
W kartezjańskim układzie współrzędnych 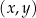 trapez
trapez 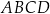 jest wpisany w okrąg o środku w punkcie
jest wpisany w okrąg o środku w punkcie 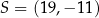 i promieniu
i promieniu 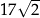 . Wierzchołek
. Wierzchołek 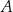 trapezu ma obie współrzędne ujemne, a odcinek
trapezu ma obie współrzędne ujemne, a odcinek 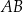 jest dłuższą z podstaw tego trapezu. Przekątna
jest dłuższą z podstaw tego trapezu. Przekątna 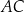 trapezu
trapezu 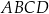 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 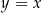 . Oblicz sinus kąta
. Oblicz sinus kąta 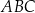 .
.
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/2293968/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 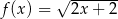 i
i 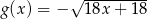 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 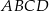 , których wierzchołki
, których wierzchołki 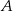 i
i 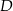 leżą na wykresie funkcji
leżą na wykresie funkcji 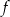 , a wierzchołki
, a wierzchołki 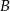 i
i 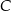 leżą na wykresie funkcji
leżą na wykresie funkcji 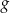 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 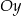 (zobacz rysunek).
(zobacz rysunek).
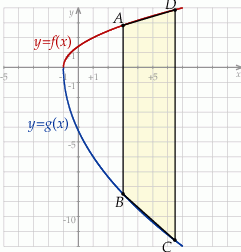
Wykaż, że jeżeli pierwsza współrzędna punktów 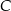 i
i 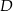 jest równa 7, a druga współrzędna punktu
jest równa 7, a druga współrzędna punktu 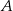 jest równa
jest równa 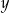 , to pole trapezu
, to pole trapezu 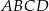 jest równe
jest równe
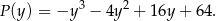
Czworokąt 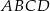 jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki
jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki 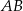 i
i 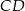 , przy czym
, przy czym 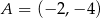 ,
, 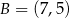 i
i 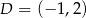 , oblicz pole oraz obwód trapezu.
, oblicz pole oraz obwód trapezu.
Dane są punkty 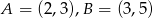 i
i 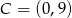 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 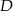 , dla którego czworokąt
, dla którego czworokąt 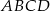 jest trapezem prostokątnym, którego kąt przy wierzchołku
jest trapezem prostokątnym, którego kąt przy wierzchołku 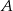 jest prosty.
jest prosty.
Punkty 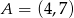 ,
, 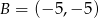 i
i 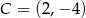 są wierzchołkami trapezu prostokątnego
są wierzchołkami trapezu prostokątnego 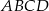 o podstawach
o podstawach 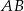 i
i 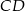 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 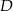 .
.
Wierzchołki trapezu 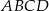 mają współrzędne:
mają współrzędne: 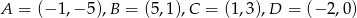 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 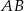 tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona
tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona 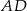 oraz
oraz 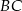 trapezu
trapezu 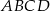 .
.
Wierzchołki trapezu 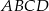 mają współrzędne:
mają współrzędne: 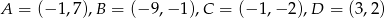 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 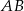 tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu
tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu 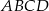 .
.
Punkty 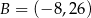 ,
, 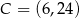 i
i 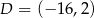 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 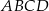 o podstawach
o podstawach 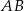 i
i 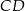 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 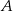 tego trapezu jeżeli wiadomo, że
tego trapezu jeżeli wiadomo, że 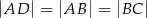 .
.
W okrąg o środku 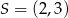 wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu
wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu 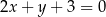 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe 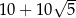 . Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
. Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
W trapezie równoramiennym 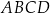 podstawa
podstawa 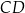 ma długość 5. Punkt
ma długość 5. Punkt 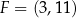 jest środkiem odcinka
jest środkiem odcinka 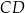 . Prosta o równaniu
. Prosta o równaniu 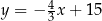 jest osią symetrii tego trapezu oraz
jest osią symetrii tego trapezu oraz 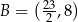 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 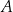 oraz pole tego trapezu.
oraz pole tego trapezu.
Odcinek o końcach 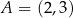 i
i 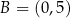 jest podstawą trapezu
jest podstawą trapezu 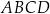 . Druga podstawa o środku w punkcie
. Druga podstawa o środku w punkcie 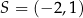 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 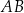 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 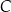 i
i 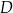 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Punkty 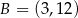 ,
, 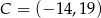 i
i 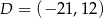 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 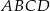 , który nie jest równoległobokiem, i w którym
, który nie jest równoległobokiem, i w którym 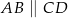 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 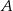 tego trapezu.
tego trapezu.
Przedłużenia ramion 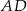 i
i 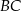 trapezu równoramiennego
trapezu równoramiennego 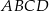 przecinają się w punkcie
przecinają się w punkcie 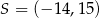 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 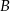 i
i 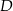 tego trapezu, jeżeli
tego trapezu, jeżeli 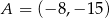 i
i 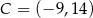 .
.
Wierzchołki czworokąta 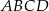 mają współrzędne:
mają współrzędne: 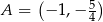 ,
, 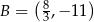 ,
, 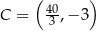 i
i  .
.
- Wykaż, że czworokąt
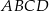 jest trapezem równoramiennym, w który można wpisać okrąg.
jest trapezem równoramiennym, w który można wpisać okrąg. - Wyznacz współrzędne punktu styczności okręgu wpisanego w czworokąt
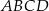 z prostą
z prostą 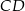 .
.
Trapez równoramienny 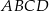 o podstawach
o podstawach 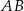 i
i 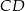 jest opisany na okręgu o równaniu
jest opisany na okręgu o równaniu 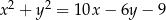 . Okrąg ten przecina boki
. Okrąg ten przecina boki 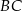 i
i 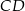 tego trapezu odpowiednio w punktach
tego trapezu odpowiednio w punktach 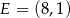 i
i 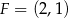 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 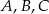 i
i 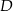 tego trapezu.
tego trapezu.
Punkty 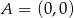 ,
, 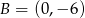 i
i 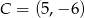 są wierzchołkami trapezu prostokątnego o polu 36 i podstawach
są wierzchołkami trapezu prostokątnego o polu 36 i podstawach 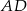 i
i 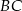 . Oblicz pole trójkąta
. Oblicz pole trójkąta 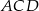 .
.
Punkty 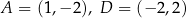 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 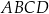 . Prosta
. Prosta 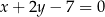 jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
Punkty 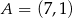 i
i 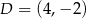 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 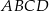 . Podstawa
. Podstawa 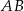 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 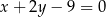 . Osią symetrii tego trapezu jest prosta o równaniu
. Osią symetrii tego trapezu jest prosta o równaniu 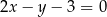 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 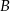 i
i  trapezu.
trapezu.
Wykaż, że czworokąt o wierzchołkach 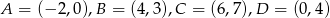 jest trapezem.
jest trapezem.
Dane są punkty 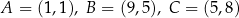 .
.
-
Wyznacz punkt
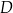 tak, aby czworokąt
tak, aby czworokąt 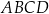 był trapezem prostokątnym, którego kąt przy wierzchołku
był trapezem prostokątnym, którego kąt przy wierzchołku 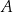 jest prosty.
jest prosty. -
Czy w ten trapez można wpisać okrąg?
Punkty 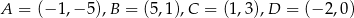 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 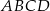 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.

