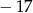Miejscami zerowymi funkcji kwadratowej 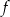 określonej wzorem
określonej wzorem 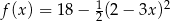 są liczby
są liczby
A) 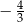 oraz
oraz 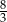 B)
B) 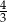 oraz
oraz 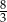 C)
C) 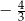 oraz
oraz 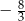 D)
D) 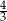 oraz
oraz 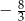
/Szkoła średnia/Zadania testowe/Równania/Kwadratowe/Dane równanie
Równanie 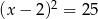 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Równanie 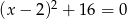 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Równanie 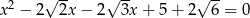
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Rozwiązaniem równania 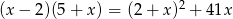 jest:
jest:
A) 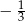 B)
B) 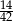 C)
C) 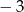 D)
D) 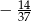
Rozwiązaniem równania 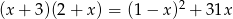 jest:
jest:
A) 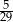 B)
B) 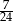 C)
C) 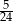 D)
D) 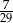
Liczba rozwiązań równania 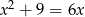 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Równanie 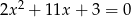
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Równanie 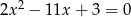
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Liczby 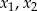 są rozwiązaniami równania
są rozwiązaniami równania 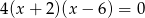 . Suma
. Suma 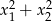 jest równa
jest równa
A) 16 B) 32 C) 40 D) 48
Funkcja kwadratowa jest określona wzorem 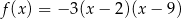 . Liczby
. Liczby 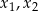 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 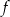 . Zatem
. Zatem
A) 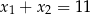 B)
B) 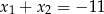 C)
C) 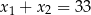 D)
D) 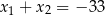
Funkcja kwadratowa jest określona wzorem 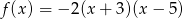 . Liczby
. Liczby 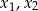 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 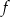 . Zatem
. Zatem
A) 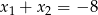 B)
B) 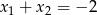 C)
C) 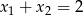 D)
D) 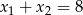
Liczby 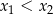 są rozwiązaniami równania
są rozwiązaniami równania 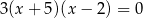 . Różnica
. Różnica 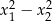 jest równa
jest równa
A) 21 B) 29 C) 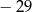 D)
D) 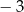
Pierwiastki 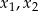 równania
równania 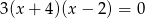 spełniają warunek
spełniają warunek
A) 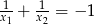 B)
B) 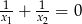 C)
C) 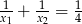 D)
D) 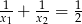
Pierwiastki 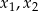 równania
równania 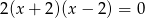 spełniają warunek
spełniają warunek
A) 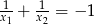 B)
B) 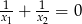 C)
C) 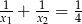 D)
D) 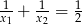
Równanie 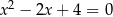
A) nie ma pierwiastków B) ma pierwiastki 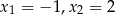
C) ma pierwiastki 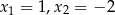 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 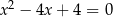
A) nie ma pierwiastków B) ma pierwiastki 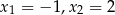
C) ma pierwiastki 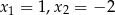 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 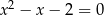
A) nie ma pierwiastków B) ma pierwiastki 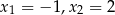
C) ma pierwiastki 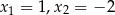 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 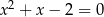
A) nie ma pierwiastków B) ma pierwiastki 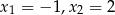
C) ma pierwiastki 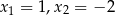 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Liczby 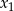 i
i 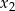 są pierwiastkami równania
są pierwiastkami równania 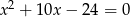 i
i 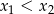 . Oblicz
. Oblicz 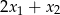 .
.
A) -22 B) -17 C) 8 D) 13
Liczby 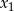 i
i 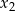 są pierwiastkami równania
są pierwiastkami równania 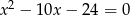 i
i 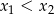 . Oblicz
. Oblicz 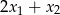 .
.
A) -22 B) -17 C) 8 D) 13
Funkcja kwadratowa jest określona wzorem 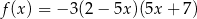 . Liczby
. Liczby 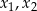 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 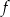 . Zatem
. Zatem
A) 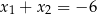 B)
B) 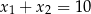 C)
C) 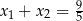 D)
D) 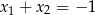
Miejscami zerowymi funkcji kwadratowej 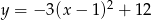 są
są
A) 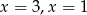 B)
B) 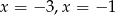 C)
C) 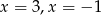 D)
D) 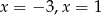
Miejscami zerowymi funkcji kwadratowej 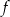 określonej wzorem
określonej wzorem 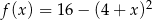 są liczby
są liczby
A) 0 oraz 4 B) 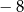 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 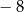 D)
D) 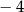 oraz 4
oraz 4
Miejscami zerowymi funkcji kwadratowej 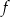 określonej wzorem
określonej wzorem 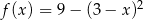 są liczby
są liczby
A) 0 oraz 3 B) 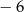 oraz 6 C) 0 oraz
oraz 6 C) 0 oraz 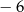 D) 0 oraz 6
D) 0 oraz 6
Funkcje kwadratowe 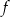 i
i 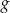 określone są wzorami
określone są wzorami 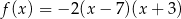 i
i 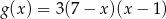 . Liczby
. Liczby 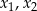 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 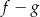 . Zatem
. Zatem
A) 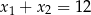 B)
B) 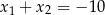 C)
C) 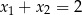 D)
D) 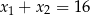
Jednym z miejsc zerowych funkcji kwadratowej 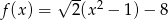 jest liczba
jest liczba
A) 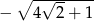 B)
B) 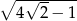 C)
C) 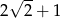 D)
D) 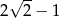
Liczby 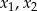 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 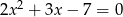 . Suma
. Suma 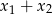 jest równa
jest równa
A) 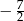 B)
B) 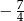 C)
C) 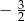 D)
D) 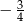
Liczby 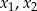 są różnymi rozwiązaniami równania
są różnymi rozwiązaniami równania 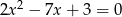 . Iloczyn
. Iloczyn 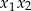 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 
Równanie 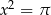
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Równanie 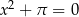
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Równanie 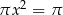
A) ma dwa pierwiastki wymierne B) ma jeden pierwiastek
C) nie ma pierwiastków D) ma dwa pierwiastki niewymierne
Kwadrat liczby  jest większy o co najmniej 4 od kwadratu liczby
jest większy o co najmniej 4 od kwadratu liczby  pomniejszonej o 2. Zatem
pomniejszonej o 2. Zatem
A) 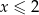 B)
B) 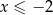 C)
C) 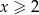 D)
D) 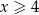
Liczba rozwiązań równania 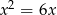 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 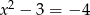 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Równanie 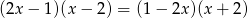 ma dwa rozwiązania. Są to liczby
ma dwa rozwiązania. Są to liczby
A) 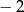 oraz
oraz 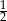 B) 0 oraz
B) 0 oraz 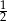 C)
C) 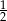 oraz 2 D)
oraz 2 D) 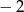 oraz 2
oraz 2
Równanie 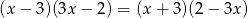 ma dwa rozwiązania. Są to liczby
ma dwa rozwiązania. Są to liczby
A) 0 oraz  B)
B) 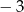 oraz
oraz  C)
C)  oraz 3 D)
oraz 3 D) 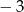 oraz 3
oraz 3
Równanie 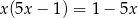 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 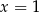 . B) dwa rozwiązania:
. B) dwa rozwiązania: 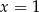 i
i 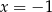 .
.
C) dwa rozwiązania: 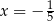 i
i 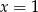 . D) dwa rozwiązania:
. D) dwa rozwiązania: 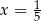 i
i 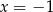 .
.
Równanie 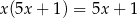 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 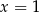 . B) dwa rozwiązania:
. B) dwa rozwiązania: 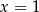 i
i 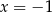 .
.
C) dwa rozwiązania: 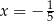 i
i 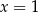 . D) dwa rozwiązania:
. D) dwa rozwiązania: 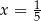 i
i 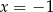 .
.
Równanie 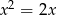 jest równoważne równaniu
jest równoważne równaniu
A) 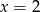 B)
B) 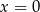 C)
C) 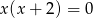 D)
D) 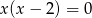
Równanie 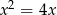 jest równoważne równaniu
jest równoważne równaniu
A) 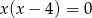 B)
B) 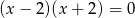 C)
C) 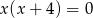 D)
D) 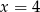
Równanie 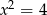 jest równoważne równaniu
jest równoważne równaniu
A) 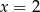 B)
B) 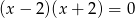 C)
C) 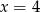 D)
D) 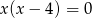
Liczby 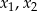 są rozwiązaniami równania
są rozwiązaniami równania 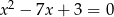 . Liczba
. Liczba 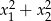 jest równa
jest równa
A) 43 B) 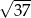 C) 55 D)
C) 55 D) 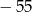
Liczby 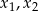 są rozwiązaniami równania
są rozwiązaniami równania 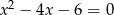 . Liczba
. Liczba 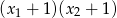 jest równa
jest równa
A) 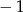 B)
B) 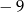 C) 11 D) 3
C) 11 D) 3
Liczby 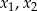 są rozwiązaniami równania
są rozwiązaniami równania 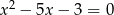 . Liczba
. Liczba 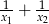 jest równa
jest równa
A) 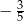 B)
B) 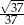 C)
C) 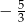 D)
D) 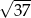
Liczby 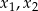 są rozwiązaniami równania
są rozwiązaniami równania 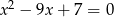 . Liczba
. Liczba 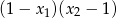 jest równa
jest równa
A) 15 B) 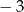 C) 1 D)
C) 1 D) 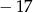
Liczby 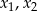 są rozwiązaniami równania
są rozwiązaniami równania 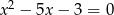 . Liczba
. Liczba 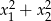 jest równa
jest równa
A) 19 B) 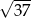 C) 31 D)
C) 31 D) 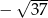
Suma kwadratów odwrotności pierwiastków równania 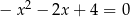 jest równa
jest równa
A) 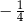 B)
B) 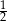 C)
C)  D)
D) 
Liczby 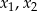 są rozwiązaniami równania
są rozwiązaniami równania 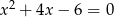 . Liczba
. Liczba 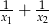 jest równa
jest równa
A) 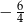 B)
B) 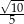 C)
C) 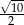 D)
D) 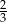
Liczby 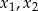 są rozwiązaniami równania
są rozwiązaniami równania 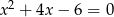 . Liczba
. Liczba 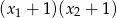 jest równa
jest równa
A) 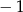 B)
B) 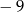 C) 11 D) 3
C) 11 D) 3
Liczby 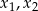 są rozwiązaniami równania
są rozwiązaniami równania 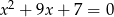 . Liczba
. Liczba 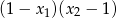 jest równa
jest równa
A) 15 B) 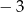 C) 1 D)
C) 1 D)