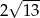Dany jest trójkąt o wierzchołkach 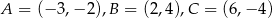 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 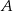 jest równa
jest równa
A) 4 B) 6 C) 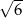 D)
D) 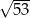
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Trójkąt/Dowolny
Dany jest trójkąt o wierzchołkach 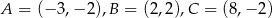 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 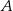 jest równa
jest równa
A) 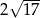 B)
B) 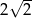 C)
C) 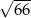 D)
D) 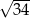
Dany jest trójkąt o wierzchołkach 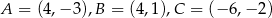 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 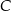 jest równa
jest równa
A) 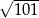 B)
B) 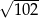 C)
C) 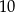 D)
D) 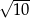
Dany jest trójkąt o wierzchołkach 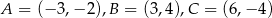 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 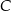 jest równa
jest równa
A) 11 B) 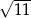 C)
C) 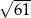 D)
D) 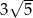
Podstawa 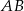 trójkąta
trójkąta 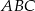 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 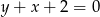 , a wierzchołek
, a wierzchołek 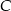 ma współrzędne
ma współrzędne 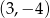 . Wysokość trójkąta opuszczona z wierzchołka
. Wysokość trójkąta opuszczona z wierzchołka 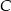 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 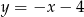 B)
B) 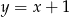 C)
C) 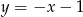 D)
D) 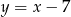
Punkt 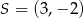 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 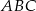 . Prosta zawierająca bok
. Prosta zawierająca bok 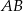 tego trójkąta ma równanie
tego trójkąta ma równanie 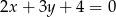 . Prosta zawierająca bok
. Prosta zawierająca bok 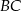 może mieć równanie
może mieć równanie
A) 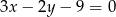 B)
B) 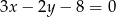 C)
C) 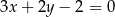 D)
D) 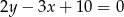
Pole trójkąta 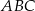 o wierzchołkach
o wierzchołkach 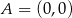 ,
, 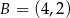 ,
, 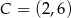 jest równe
jest równe
A) 5 B) 10 C) 15 D) 20
Pole trójkąta 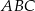 o wierzchołkach
o wierzchołkach 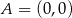 ,
, 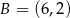 ,
, 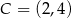 jest równe
jest równe
A) 10 B) 5 C) 20 D) 15
Na bokach 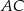 i
i 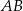 trójkąta
trójkąta 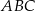 o wierzchołkach
o wierzchołkach 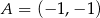 ,
, 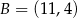 i
i 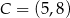 , wybrano punkty
, wybrano punkty 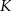 i
i 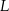 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 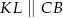 . Pole trapezu
. Pole trapezu 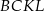 stanowi
stanowi 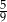 pola trójkąta
pola trójkąta 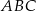 . Zatem
. Zatem
A) 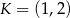 B)
B) 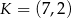 C)
C) 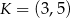 D)
D) 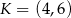
W okrąg o równaniu 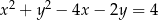 wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze
wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze 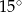 . Podstawa tego trójkąta ma długość
. Podstawa tego trójkąta ma długość
A) 1,5 B) 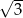 C) 3 D)
C) 3 D) 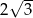
W układzie współrzędnych dany jest trójkąt o wierzchołkach 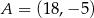 ,
, 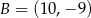 i
i 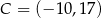 . Na boku
. Na boku 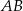 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 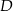 tak, że pole trójkąta
tak, że pole trójkąta 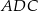 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 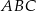 . Wówczas
. Wówczas
A) 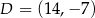 B)
B) 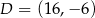 C)
C) 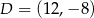 D)
D) 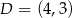
Punkty 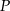 i
i 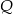 są środkami boków
są środkami boków 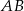 i
i 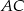 trójkąta
trójkąta 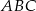 . Bok
. Bok 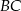 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 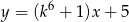 , a punkty
, a punkty 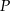 i
i 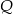 leżą na prostej
leżą na prostej 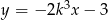 . Wynika stąd, że
. Wynika stąd, że
A) 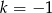 B)
B) 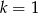 C)
C) 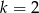 D)
D) 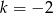
Wiadomo, że 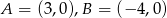 i punkty
i punkty 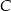 i
i 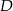 leżą na prostej
leżą na prostej 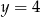 . Pole trójkąta
. Pole trójkąta 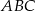 jest równe
jest równe 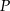 , a pole trójkąta
, a pole trójkąta 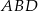 jest równe
jest równe 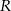 . Zatem
. Zatem
A) 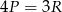 B)
B) 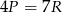 C)
C) 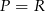 D)
D) 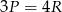
Wiadomo, że 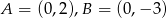 , a punkty
, a punkty 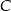 i
i 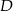 leżą na prostej
leżą na prostej 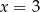 . Pole trójkąta
. Pole trójkąta 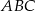 jest równe
jest równe 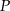 , a pole trójkąta
, a pole trójkąta 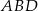 jest równe
jest równe 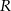 . Zatem
. Zatem
A) 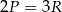 B)
B) 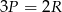 C)
C) 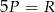 D)
D) 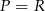
Wiadomo, że 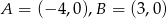 i punkty
i punkty 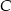 i
i 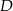 leżą na prostej
leżą na prostej 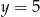 . Pole trójkąta
. Pole trójkąta 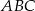 jest równe
jest równe 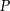 , a pole trójkąta
, a pole trójkąta 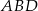 jest równe
jest równe 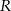 . Zatem
. Zatem
A) 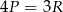 B)
B) 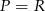 C)
C) 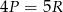 D)
D) 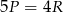
Dane są punkty 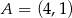 ,
, 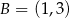 ,
, 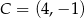 . Pole trójkąta
. Pole trójkąta 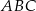 jest równe
jest równe
A) 3 B) 6 C) 8 D) 16
Dane są punkty 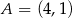 ,
, 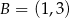 ,
, 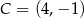 . Pole trójkąta
. Pole trójkąta 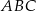 jest równe
jest równe
A) 2 B) 3 C) 6 D) 12
Dany jest trójkąt 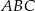 , w którym
, w którym 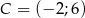 ,
, ![−→ CB = [4;− 2]](https://img.zadania.info/zad/8646781/HzadT2x.gif) oraz środek ciężkości
oraz środek ciężkości 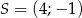 . Współrzędne wierzchołka
. Współrzędne wierzchołka 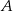 są równe
są równe
A) 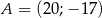 B)
B) 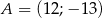 C)
C) 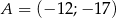 D)
D) 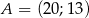
Punkt przecięcia środkowych w trójkącie 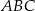 , gdzie
, gdzie 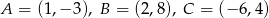 ma współrzędne:
ma współrzędne:
A) 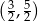 B)
B) 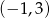 C)
C) 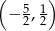 D)
D) 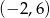
Na płaszczyźnie dane są punkty: 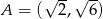 ,
, 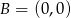 i
i 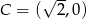 . Kąt
. Kąt 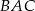 jest równy
jest równy
A) 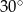 B)
B) 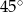 C)
C) 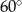 D)
D) 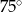
Na płaszczyźnie dane są punkty: 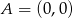 ,
, 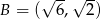 i
i 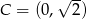 . Kąt
. Kąt 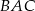 jest równy
jest równy
A) 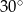 B)
B) 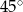 C)
C) 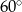 D)
D) 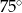
Na płaszczyźnie dane są punkty: 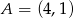 ,
, 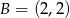 i
i 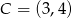 . Kąt
. Kąt 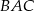 jest równy
jest równy
A) 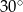 B)
B) 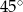 C)
C) 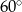 D)
D) 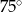
Pole trójkąta wyznaczonego przez wykresy funkcji 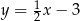 i
i 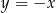 oraz oś
oraz oś 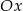 jest równe
jest równe
A) 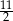 B)
B) 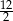 C)
C) 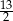 D)
D) 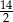
Pole trójkąta wyznaczonego przez wykresy funkcji 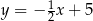 i
i 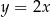 oraz oś
oraz oś 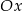 jest równe
jest równe
A) 20 B) 10 C) 32 D) 40
W trójkącie 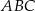 dane są wierzchołki
dane są wierzchołki 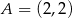 ,
, 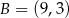 ,
, 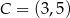 . Trójkąt
. Trójkąt 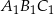 jest obrazem trójkąta
jest obrazem trójkąta 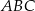 w jednokładności o środku
w jednokładności o środku 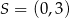 i skali
i skali 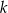 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 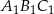 ma długość
ma długość 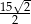 . Skala jednokładności
. Skala jednokładności 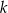 wynosi
wynosi
A) 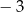 B)
B) 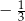 C)
C) 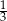 D) 3
D) 3
Punkt 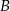 jest symetryczny do punktu
jest symetryczny do punktu 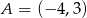 względem osi
względem osi 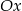 układu współrzędnych, a punkt
układu współrzędnych, a punkt 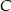 jest symetryczny do punktu
jest symetryczny do punktu 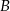 względem osi
względem osi 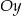 . Zatem trójkąt
. Zatem trójkąt 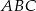 jest
jest
A) równoboczny
B) prostokątny i równoramienny
C) prostokątny i żaden z jego kątów nie jest równy 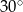
D) prostokątny z kątem ostrym równym 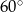
Wierzchołki trójkąta 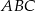 mają współrzędne
mają współrzędne 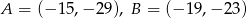 i
i 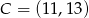 . Bok
. Bok 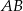 trójkąta
trójkąta 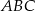 ma długość
ma długość
A) 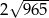 B)
B) 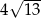 C)
C) 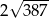 D)
D)