Krótsza podstawa trapezu ma długość 2, a ramiona długości 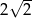 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 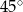 i
i 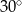 . Oblicz pole trapezu.
. Oblicz pole trapezu.
/Szkoła podstawowa/Geometria/Czworokąty/Trapez
Krótsza podstawa trapezu ma długość 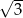 , a ramiona długości
, a ramiona długości 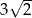 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 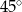 i
i 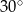 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.
Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
Wykaż, że w dowolnym trapezie suma długości ramion jest mniejsza od sumy długości przekątnych.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego wynosi 50 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 5 cm i 12 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Obwód trapezu równoramiennego jest równy 56 cm, ramię ma długość 15 cm, a różnica długości podstaw wynosi 18 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Podstawy trapezu równoramiennego 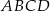 mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe
mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe 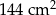 . Oblicz obwód trapezu
. Oblicz obwód trapezu 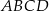 .
.
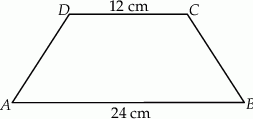
W trapezie 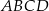 mamy
mamy 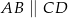 oraz
oraz 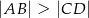 . Punkt
. Punkt 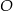 jest środkiem ramienia
jest środkiem ramienia 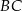 , a punkt
, a punkt 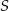 jest punktem wspólnym prostych
jest punktem wspólnym prostych 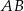
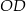 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 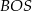 jest równe polu trójkąta
jest równe polu trójkąta 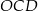 .
.
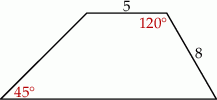
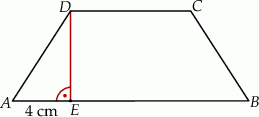
Oblicz pole i obwód trapezu przedstawionego na rysunku.
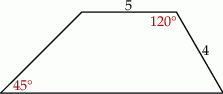
Oblicz pole i obwód trapezu przedstawionego na rysunku.
Paweł wyciął z kartonu trójkąt prostokątny 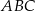 o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt  wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez  (rysunek II).
(rysunek II).
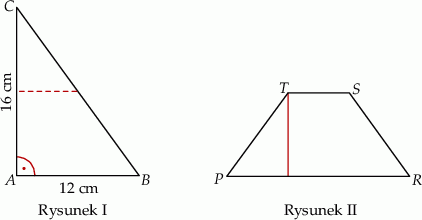
Oblicz różnicę obwodów trójkąta  i trapezu
i trapezu 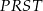 .
.
Karol wyciął z kartonu trójkąt prostokątny 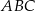 (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
(rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt 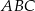 wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez 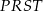 o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
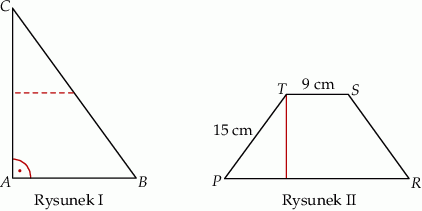
Oblicz różnicę obwodów trójkąta 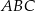 i trapezu
i trapezu 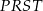 .
.
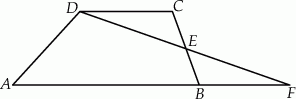
Na rysunku przedstawiono trapez 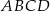 i trójkąt
i trójkąt 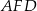 . Punkt
. Punkt 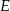 leży w połowie odcinka
leży w połowie odcinka 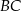 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 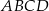 i pole trójkąta
i pole trójkąta  są równe.
są równe.
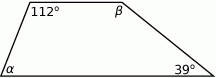
Oblicz miary kątów  i
i  w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku.
Oblicz miary kątów  i
i 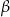 w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku.
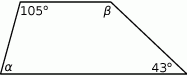
Oblicz miary kątów  i
i 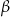 w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku.

Oblicz miary kątów  i
i 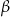 w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku.

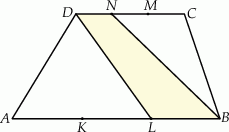
Punkty 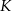 i
i 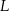 dzielą podstawę
dzielą podstawę 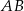 trapezu
trapezu 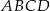 na trzy równe części, a punkty
na trzy równe części, a punkty 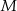 i
i 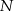 dzielą podstawę
dzielą podstawę 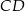 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 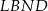 jest równe
jest równe 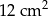 . Oblicz pole trapezu
. Oblicz pole trapezu 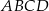 .
.
W trapezie 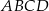 punkt
punkt 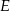 jest środkiem ramienia
jest środkiem ramienia 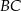 . Z wierzchołka
. Z wierzchołka 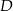 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 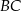 w punkcie
w punkcie 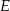 . Proste
. Proste 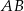 i
i 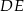 przecinają się w punkcie
przecinają się w punkcie 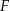 (zobacz rysunek). Wykaż, że
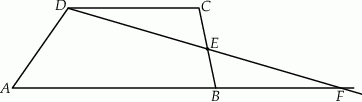
(zobacz rysunek). Wykaż, że 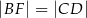 .
.
Boki trapezu równoramiennego mają długości 5 cm, 6 cm, 5 cm i 12 cm. Oblicz pole tego trapezu.
Boki trapezu równoramiennego mają długości 10 cm, 5 cm, 10 cm i 17 cm. Oblicz pole tego trapezu.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 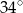 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 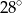 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
Pole trapezu przedstawionego na rysunku jest równe 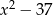 . Oblicz
. Oblicz  .
.
Trapez równoramienny 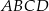 , którego pole jest równe
, którego pole jest równe 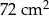 , podzielono na trójkąt
, podzielono na trójkąt 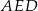 i trapez
i trapez 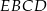 . Odcinek
. Odcinek 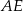 ma długość równą 4 cm, a odcinek
ma długość równą 4 cm, a odcinek 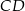 jest od niego 2 razy dłuższy. Oblicz pole trójkąta
jest od niego 2 razy dłuższy. Oblicz pole trójkąta 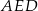 .
.
W prostokącie 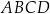 bok
bok 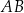 jest cztery razy dłuższy od boku
jest cztery razy dłuższy od boku 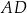 . Punkty
. Punkty 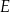 i
i 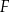 dzielą odcinek
dzielą odcinek 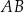 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
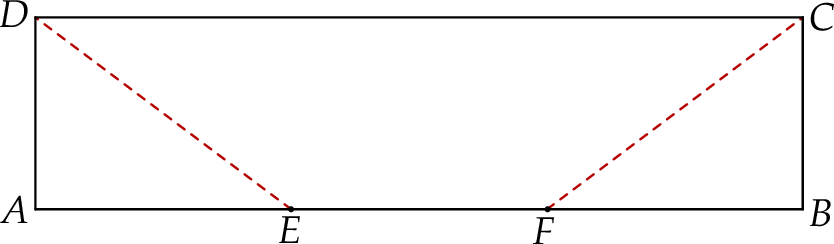
Oblicz pole trapezu 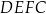 jeżeli wiadomo, że jego obwód jest równy 52 cm.
jeżeli wiadomo, że jego obwód jest równy 52 cm.
Wyprowadź wzór na pole trapezu ze wzorów na pole równoległoboku i trójkąta.
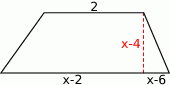
Oblicz pole i obwód trapezu prostokątnego przedstawionego na rysunku.
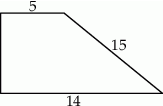
Oblicz pole i obwód trapezu prostokątnego przedstawionego na rysunku.
W trapezie 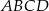 podstawy
podstawy 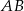 i
i 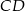 oraz ramię
oraz ramię 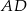 mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię
mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię 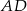 , by przecięło się z przedłużeniem ramienia
, by przecięło się z przedłużeniem ramienia 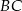 ?
?

