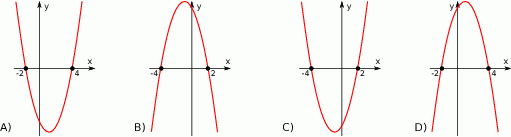
Na rysunku przedstawiono fragment wykresu funkcji 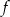 określonej wzorem
określonej wzorem 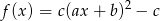 .
.
Współczynniki 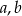 i
i  spełniają warunki:
spełniają warunki:
A) 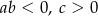 B)
B) 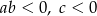 C)
C) 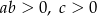 D)
D) 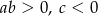
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment wykresu funkcji 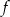 określonej wzorem
określonej wzorem 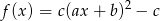 .
.

Współczynniki 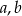 i
i  spełniają warunki:
spełniają warunki:
A) 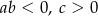 B)
B) 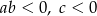 C)
C) 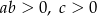 D)
D) 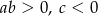
Funkcja kwadratowa 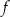 jest określona wzorem
jest określona wzorem 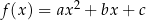 , gdzie
, gdzie 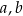 oraz
oraz  są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 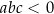 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 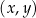 . Fragment wykresu funkcji
. Fragment wykresu funkcji 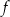 przedstawiono na rysunku
przedstawiono na rysunku
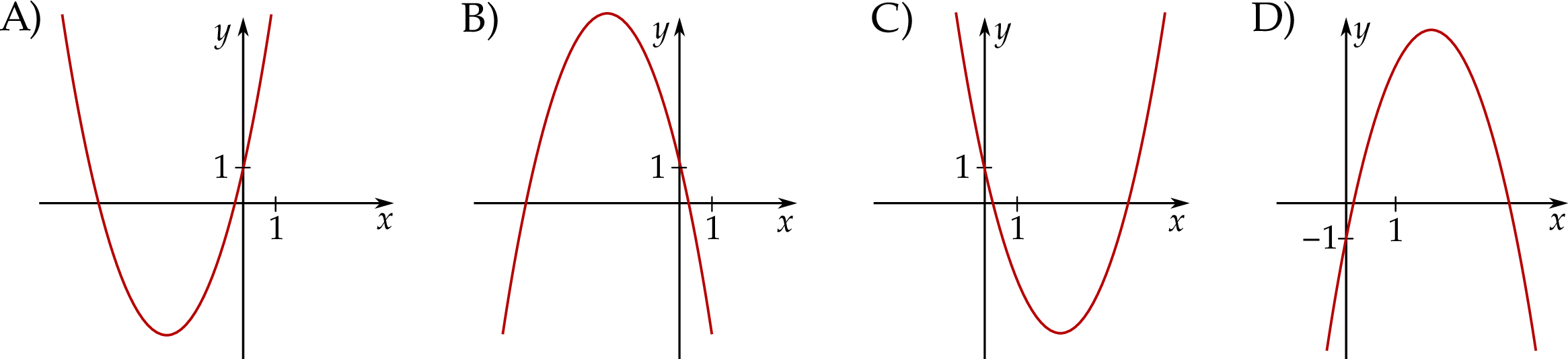
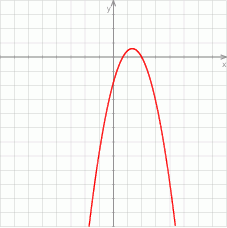
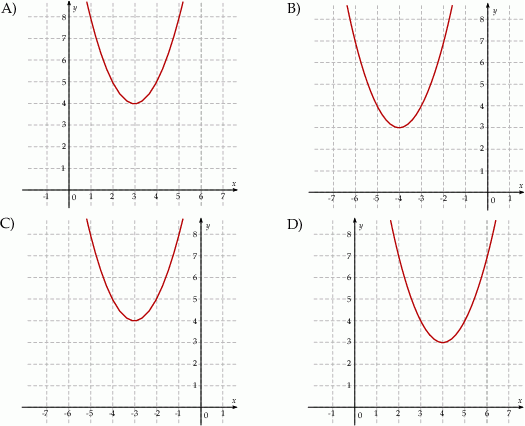
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 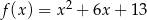 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 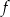 .
.
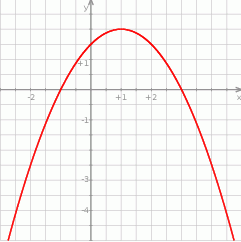
Funkcja 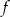 jest określona wzorem
jest określona wzorem
A) 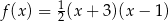 B)
B) 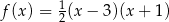
C) 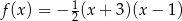 D)
D) 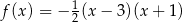
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 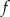 .
.
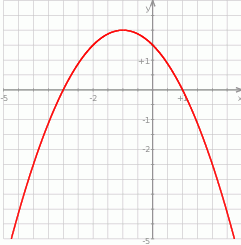
Funkcja 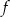 jest określona wzorem
jest określona wzorem
A) 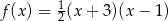 B)
B) 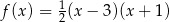
C) 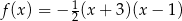 D)
D) 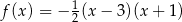
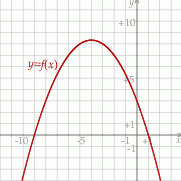
Dana jest funkcja kwadratowa 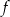 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji  jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja 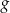 jest określona za pomocą funkcji
jest określona za pomocą funkcji 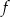 następująco:
następująco: 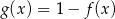 . Wykres funkcji
. Wykres funkcji 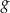 przedstawiono na rysunku
przedstawiono na rysunku
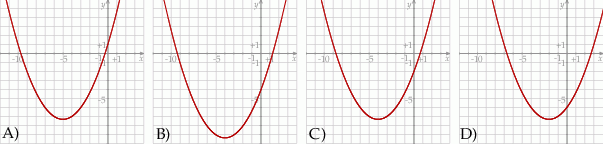
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 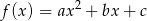 , której miejsca zerowe to:
, której miejsca zerowe to: 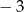 i 1.
i 1.
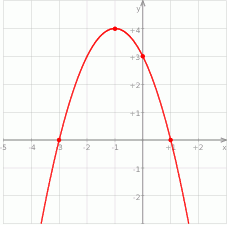
Współczynnik  we wzorze funkcji
we wzorze funkcji 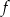 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 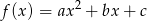 , której miejsca zerowe to:
, której miejsca zerowe to: 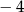 i 2.
i 2.
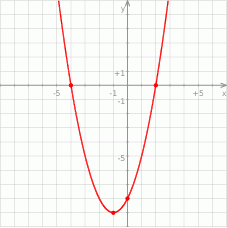
Współczynnik  we wzorze funkcji
we wzorze funkcji 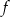 jest równy
jest równy
A) 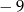 B)
B) 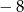 C) 4 D)
C) 4 D) 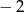
W kartezjańskim układzie współrzędnych 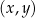 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 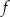 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 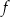 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
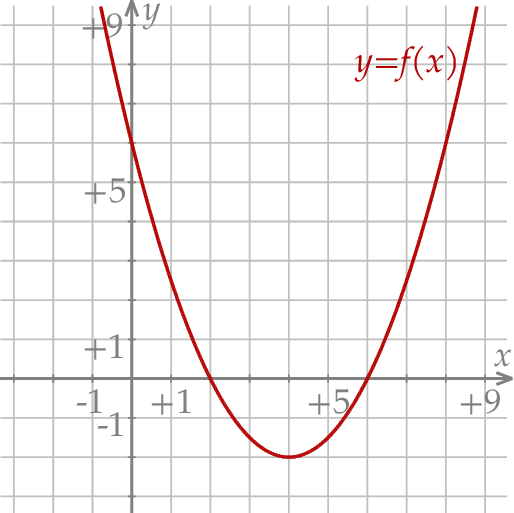
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 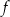 można przedstawić w postaci:
można przedstawić w postaci:
A) 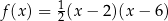 B)
B) 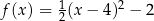
C) 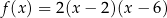 D)
D) 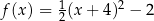
E) 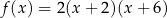 F)
F) 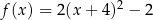
W kartezjańskim układzie współrzędnych 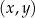 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 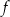 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 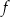 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
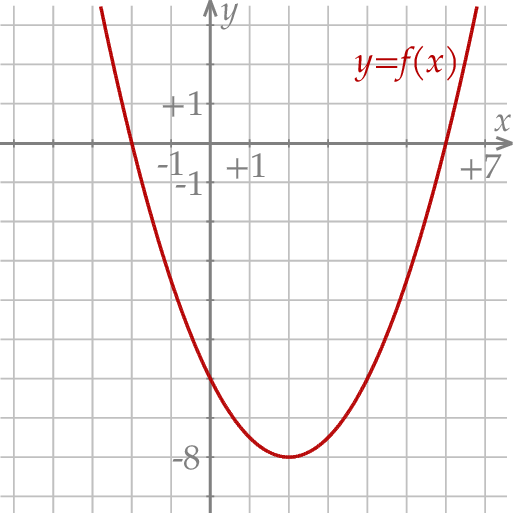
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 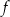 można przedstawić w postaci:
można przedstawić w postaci:
A) 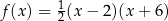 B)
B) 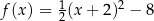
C) 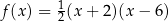 D)
D) 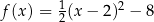
E) 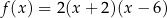 F)
F) 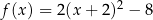
W kartezjańskim układzie współrzędnych 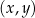 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 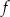 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 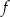 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
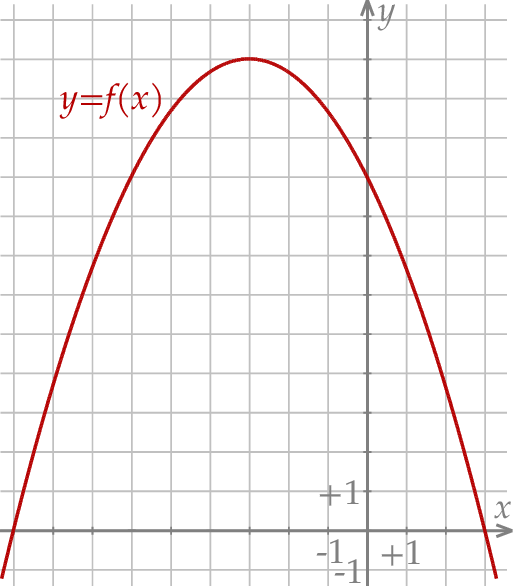
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 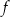 można przedstawić w postaci:
można przedstawić w postaci:
A) 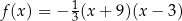 B)
B) 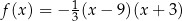
C) 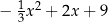 D)
D) 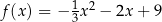
E) 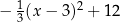 F)
F) 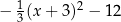
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 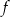 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 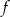 należy punkt
należy punkt 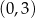 . Prosta o równaniu
. Prosta o równaniu 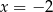 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 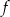 .
.
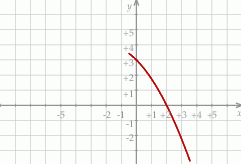
Drugim miejscem zerowym funkcji 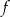 jest liczba
jest liczba
A) 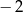 B)
B) 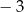 C)
C) 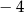 D)
D) 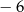
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 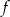 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 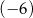 . Do wykresu funkcji
. Do wykresu funkcji 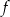 należy punkt
należy punkt 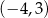 . Prosta o równaniu
. Prosta o równaniu 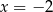 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 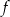 .
.
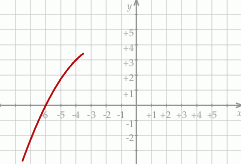
Drugim miejscem zerowym funkcji 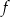 jest liczba
jest liczba
A) 2 B) 1 C) 0 D) 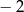
Funkcja kwadratowa 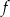 jest określona wzorem
jest określona wzorem 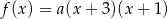 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 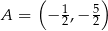 .
.
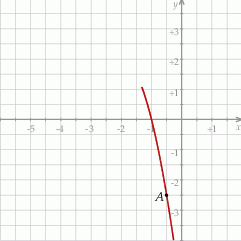
Osią symetrii paraboli będącej wykresem funkcji 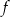 jest prosta o równaniu
jest prosta o równaniu
A) 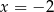 B)
B) 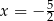 C)
C) 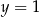 D)
D) 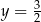
Funkcja kwadratowa 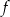 jest określona wzorem
jest określona wzorem 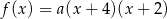 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 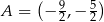 .
.
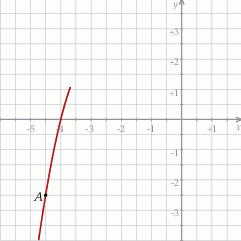
Najmniejsza wartość funkcji 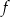 w przedziale
w przedziale 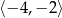 jest równa
jest równa
A) 0 B) 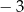 C)
C) 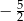 D)
D) 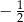
Dane są funkcje 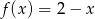 oraz
oraz 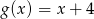 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 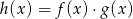 .
.
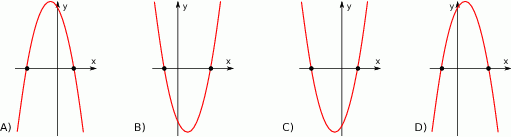
Dane są funkcje 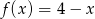 oraz
oraz 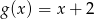 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 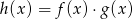 .
.
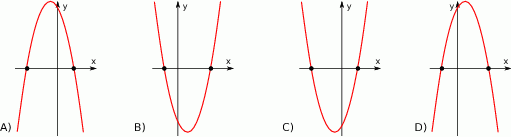
Który z rysunków może przedstawiać wykres funkcji kwadratowej 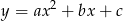 takiej, że
takiej, że 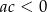 ?
?
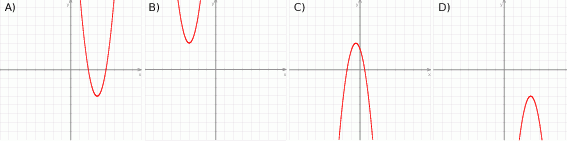
Który z rysunków może przedstawiać wykres funkcji kwadratowej 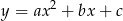 takiej, że
takiej, że 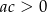 ?
?
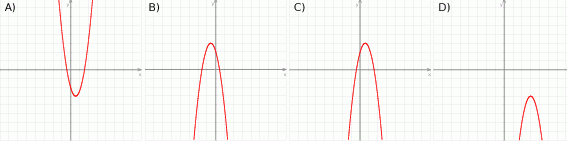
Wykresem funkcji 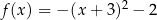 jest:
jest:
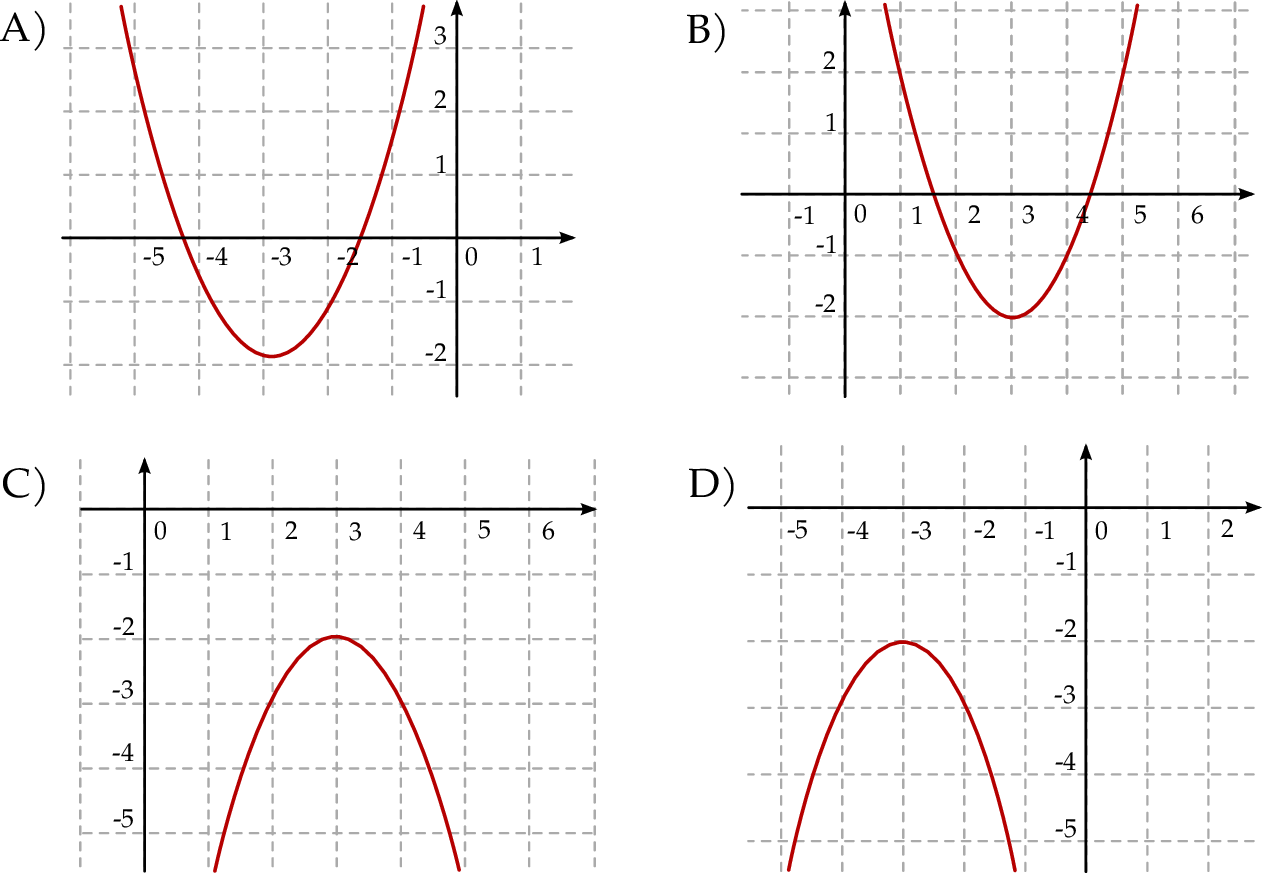
Wykres funkcji 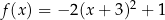 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
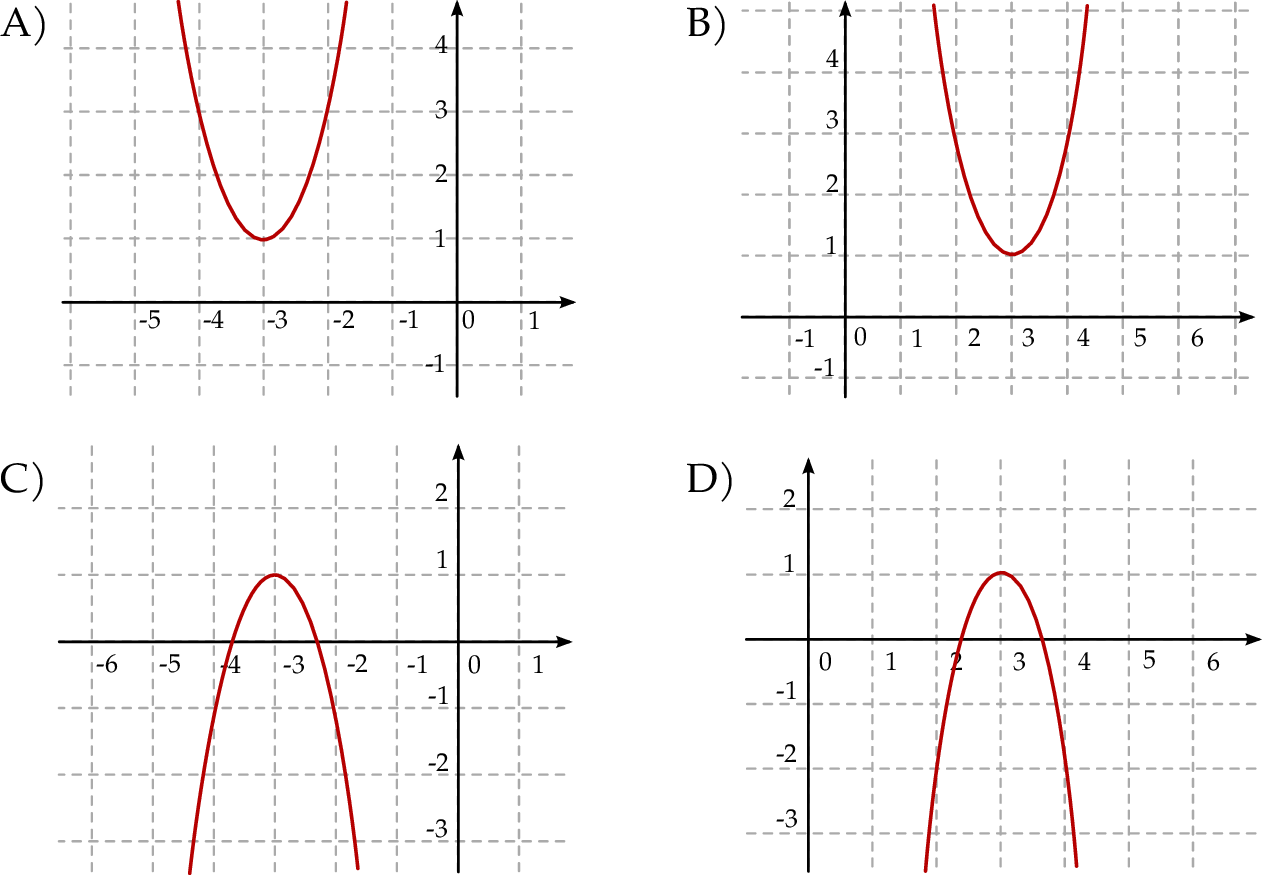
Funkcja kwadratowa 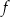 jest określona wzorem
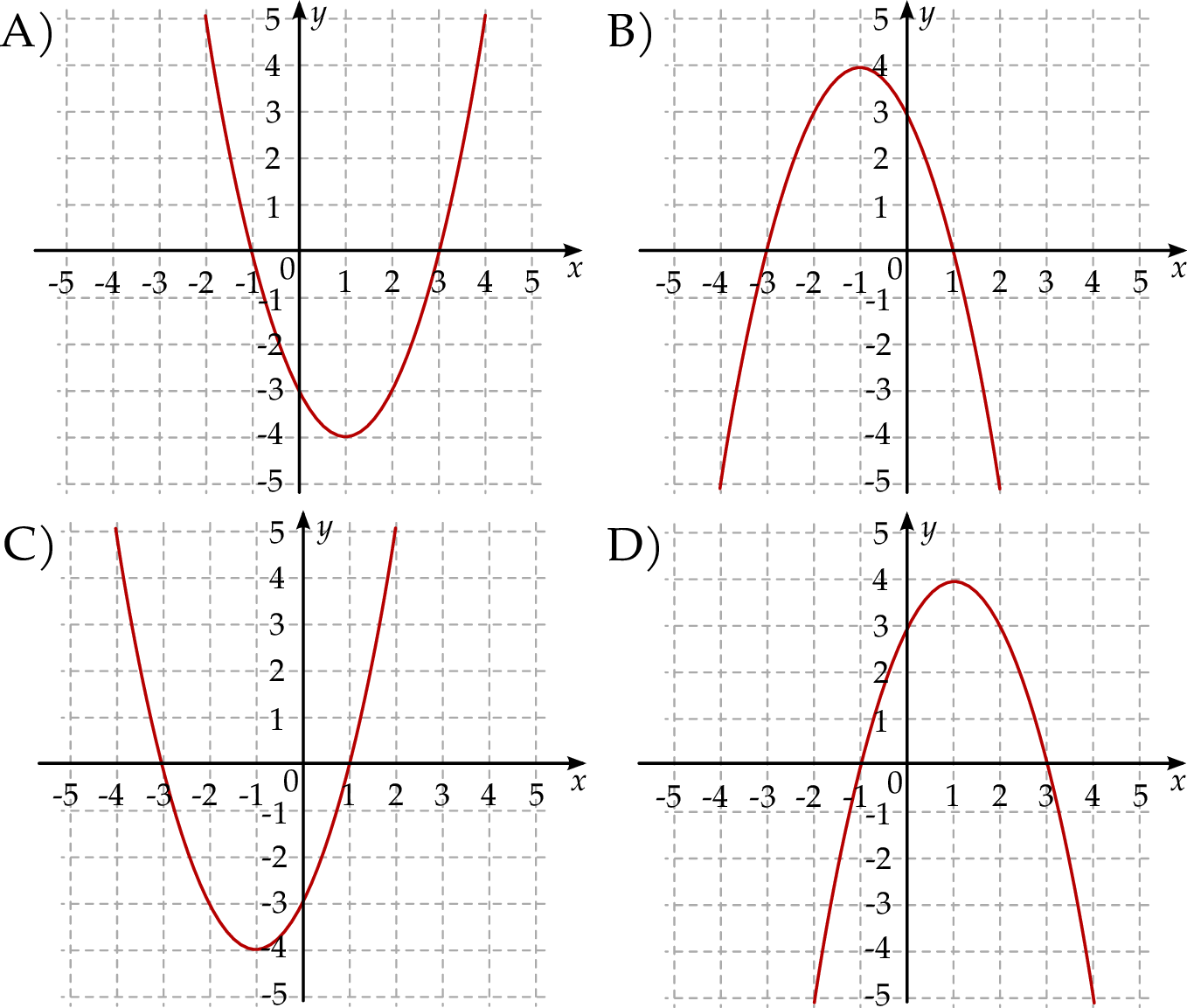
jest określona wzorem 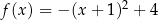 . Fragment wykresu funkcji
. Fragment wykresu funkcji 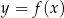 przedstawiono na rysunku
przedstawiono na rysunku
Na rysunku przedstawiono wykres funkcji kwadratowej postaci 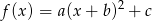 .
.
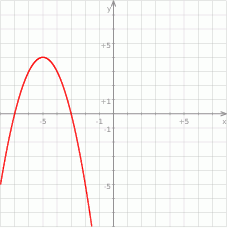
Zatem
A) 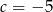 B)
B) 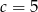 C)
C) 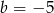 D)
D) 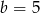
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
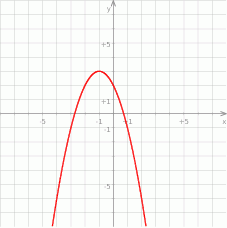
A) 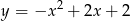 B)
B) 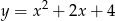 C)
C) 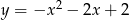 D)
D) 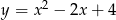
Wzorem funkcji kwadratowej 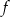 , której fragment wykresu przedstawiono na rysunku jest:
, której fragment wykresu przedstawiono na rysunku jest:
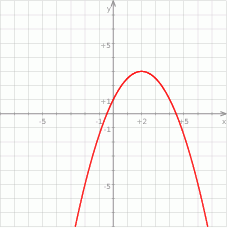
A) 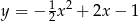 B)
B) 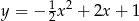 C)
C) 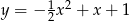 D)
D) 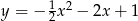
Dany jest fragment wykresu pewnej funkcji kwadratowej 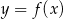 . Funkcja ta ma wzór
. Funkcja ta ma wzór
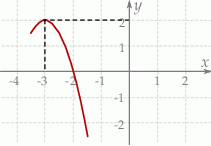
A) 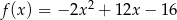 B)
B) 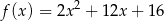
C) 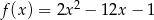 D)
D) 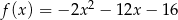
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 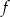 .
.
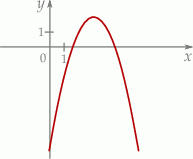
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 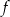 .
.
A) 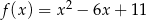 B)
B) 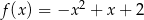
C) 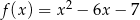 D)
D) 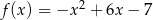
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 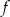 .
.
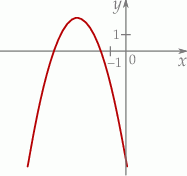
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 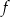 .
.
A) 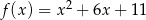 B)
B) 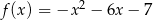
C) 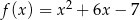 D)
D) 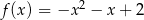
Jaki jest wzór funkcji kwadratowej, której wykres przedstawiono na rysunku?
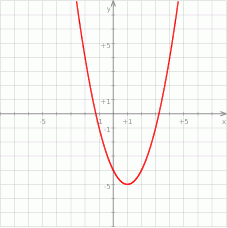
A) 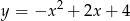 B)
B) 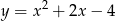 C)
C) 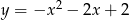 D)
D) 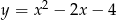
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 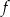 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 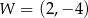 . Liczby 0 i 4 to miejsca zerowe funkcji
. Liczby 0 i 4 to miejsca zerowe funkcji 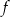 .
.
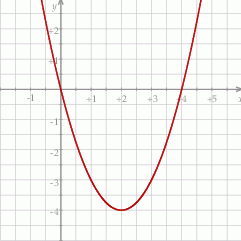
Osią symetrii wykresu funkcji 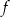 jest prosta o równaniu
jest prosta o równaniu
A) 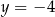 B)
B) 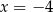 C)
C) 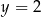 D)
D) 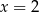
Funkcja kwadratowa 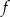 jest określona wzorem
jest określona wzorem 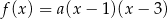 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 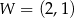 .
.
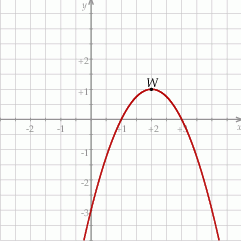
Osią symetrii paraboli będącej wykresem funkcji 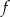 jest prosta o równaniu
jest prosta o równaniu
A) 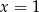 B)
B) 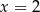 C)
C) 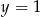 D)
D) 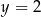
Funkcja kwadratowa 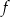 jest określona wzorem
jest określona wzorem 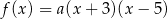 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 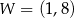 .
.
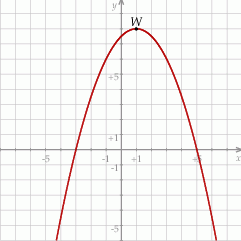
Osią symetrii paraboli będącej wykresem funkcji 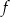 jest prosta o równaniu
jest prosta o równaniu
A) 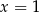 B)
B) 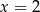 C)
C) 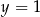 D)
D) 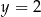
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 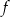 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 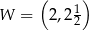 . Liczby
. Liczby 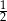 i
i 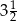 to miejsca zerowe funkcji
to miejsca zerowe funkcji 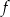 .
.
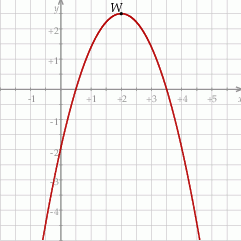
Osią symetrii wykresu funkcji 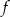 jest prosta o równaniu
jest prosta o równaniu
A) 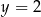 B)
B) 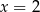 C)
C) 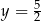 D)
D) 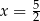
W kartezjańskim układzie współrzędnych 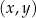 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 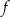 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 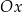 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite.
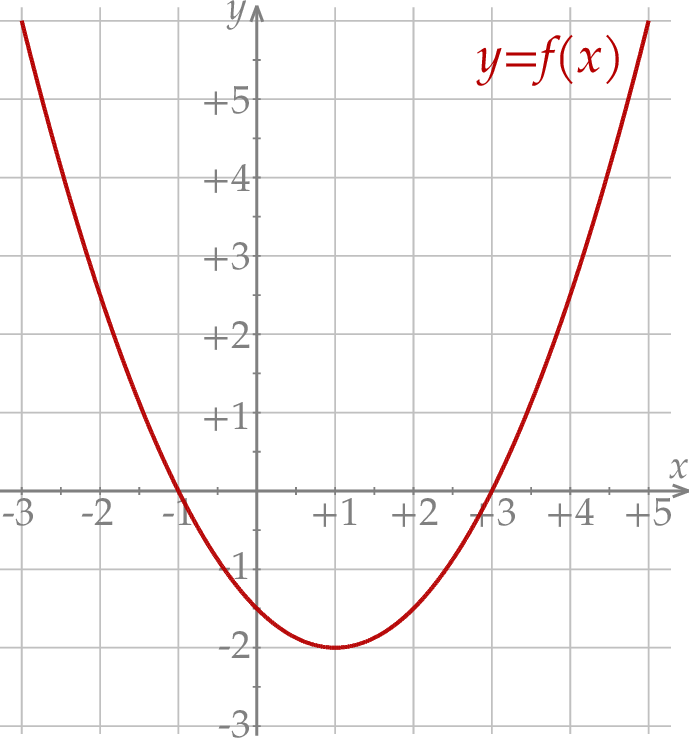
Osią symetrii wykresu funkcji 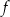 jest prosta o równaniu
jest prosta o równaniu
A) 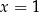 B)
B) 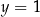 C)
C) 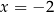 D)
D) 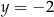
Na rysunku przedstawiono fragmenty dwóch wykresów: funkcji liniowej 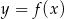 i funkcji
i funkcji ![y = g(x) = [f (x)]2](https://img.zadania.info/zad/3591919/HzadT1x.gif) . Oba wykresy przechodzą przez punkty o współrzędnych
. Oba wykresy przechodzą przez punkty o współrzędnych 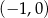 i
i 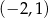 .
.
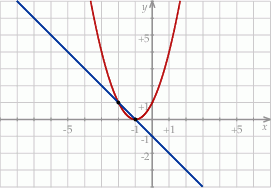
Zbiorem wartości funkcji 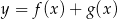 jest przedział
jest przedział
A) 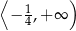 B)
B) 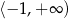 C)
C) 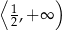 D)
D) 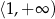
W kartezjańskim układzie współrzędnych 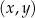 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 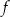 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 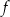 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
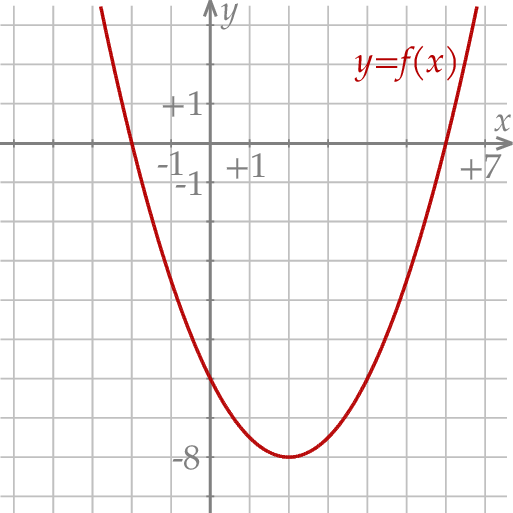
Funkcja kwadratowa 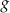 jest określona za pomocą funkcji
jest określona za pomocą funkcji 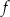 następująco:
następująco: 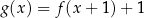 . Fragment wykresu funkcji
. Fragment wykresu funkcji  przedstawiono na rysunku
przedstawiono na rysunku
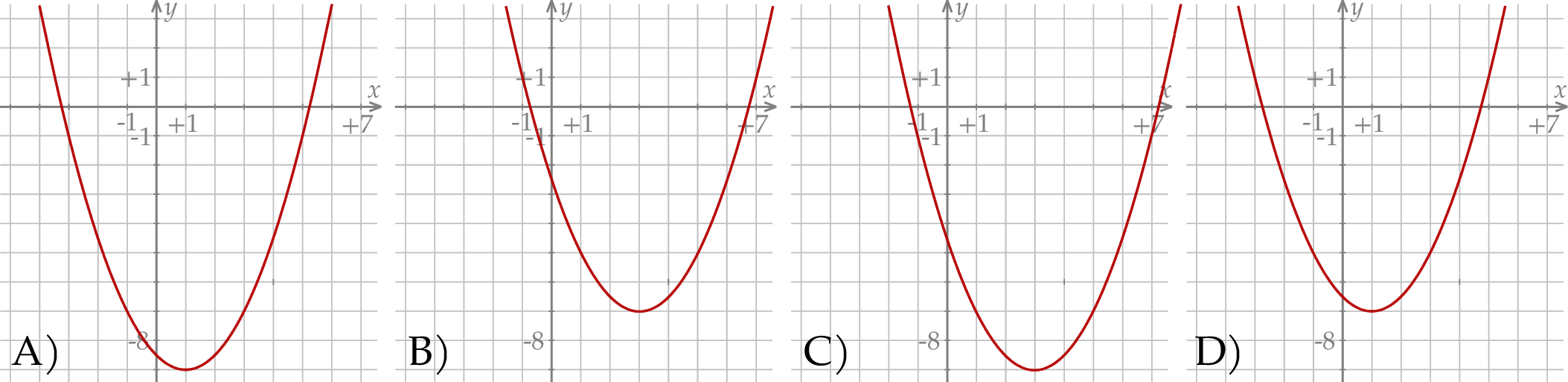
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 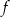 określonej wzorem
określonej wzorem 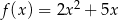 .
.
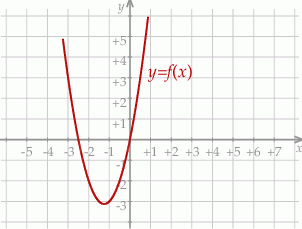
 jest określona wzorem
jest określona wzorem 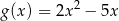 . Wykres funkcji
. Wykres funkcji 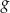 jest
jest 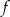 względem osi
względem osi 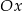 .
. 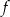 względem osi
względem osi 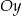 .
. 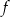 względem początku układu współrzędnych.
względem początku układu współrzędnych. 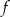 o 10 jednostek w kierunku przeciwnym do zwrotu osi
o 10 jednostek w kierunku przeciwnym do zwrotu osi 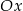 .
. Dane są funkcje liniowe 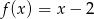 oraz
oraz 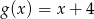 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 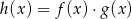 .
.
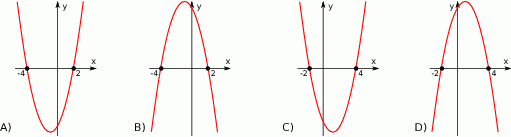
Dane są funkcje liniowe 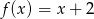 oraz
oraz 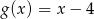 określone dla wszystkich liczb rzeczywistych
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 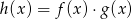 .
.