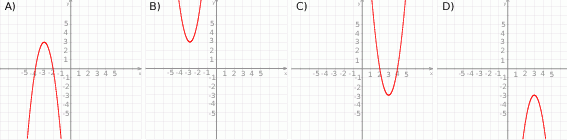
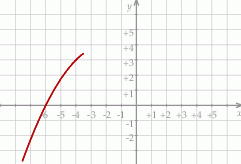
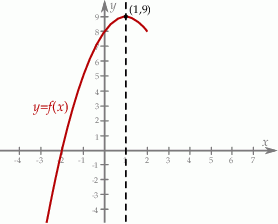
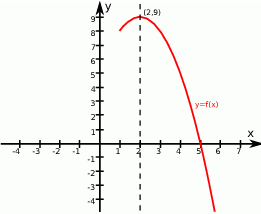
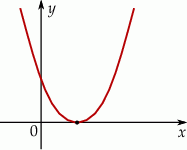
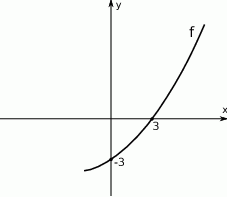
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 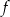 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 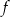 należy punkt
należy punkt 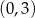 . Prosta o równaniu
. Prosta o równaniu 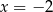 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 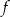 .
.
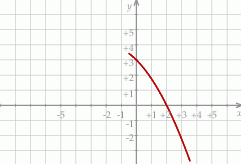
Wartość funkcji 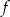 dla argumentu
dla argumentu 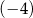 jest równa
jest równa
A) 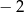 B) 0 C) 3 D) 4
B) 0 C) 3 D) 4

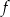 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 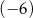 . Do wykresu funkcji
. Do wykresu funkcji 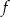 należy punkt
należy punkt 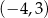 . Prosta o równaniu
. Prosta o równaniu 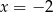 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 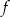 .
. 
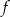 dla argumentu 0 jest równa
dla argumentu 0 jest równa 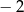
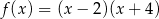 .
. 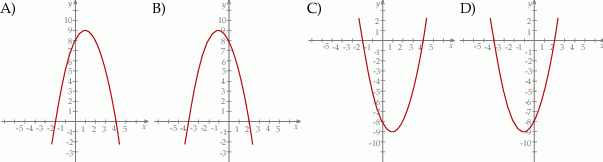
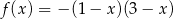 . Wskaż ten rysunek.
. Wskaż ten rysunek. 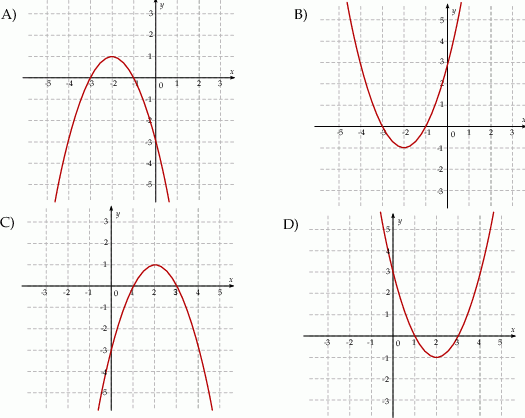
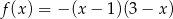 . Wskaż ten rysunek.
. Wskaż ten rysunek. 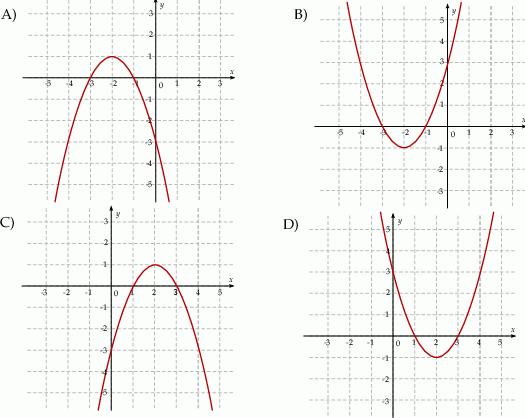
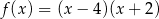 .
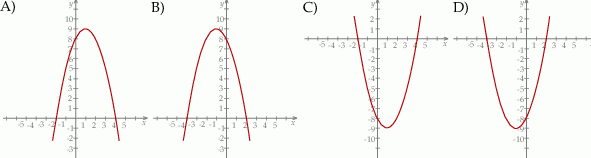
. 
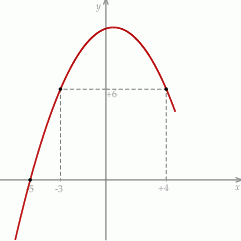
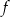 , określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty
, określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty 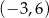 i
i 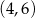 , a liczba
, a liczba 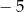 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 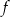 .
. 
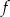 jest liczba
jest liczba 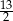
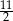
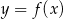 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe. 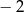 oraz 4.
oraz 4. 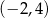 .
. 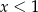 .
. 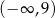 .
. 
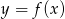 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe. 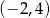 .
. 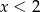 .
. 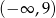 .
. 
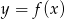 wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe. 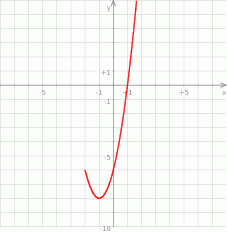
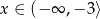 to
to 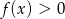 .
. 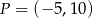 .
. 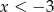 .
. 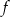 są liczby: 1 oraz -4.
są liczby: 1 oraz -4. 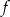 , określonej na zbiorze
, określonej na zbiorze 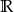 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe. 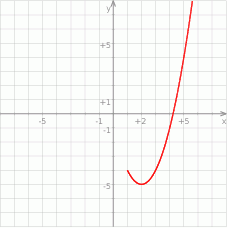
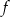 przecina oś
przecina oś 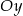 w punkcie
w punkcie 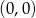 .
. 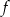 przyjmuje wartość 2.
przyjmuje wartość 2. 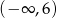 .
. 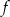 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 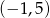 .
.  wskaż, które zdanie jest prawdziwe.
wskaż, które zdanie jest prawdziwe. 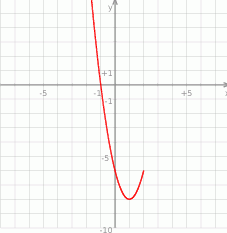
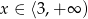 to
to 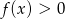 .
. 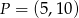 .
. 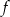 są liczby: -1 oraz 4.
są liczby: -1 oraz 4. 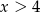 .
. 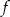 , określonej na zbiorze
, określonej na zbiorze  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe. 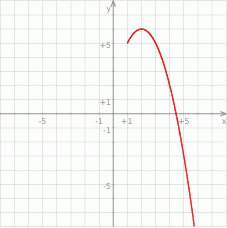
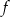 przecina oś
przecina oś 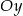 w punkcie
w punkcie 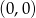 .
. 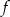 przyjmuje wartość 2.
przyjmuje wartość 2. 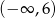 .
. 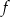 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 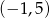 .
. 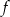 , określonej na zbiorze
, określonej na zbiorze 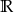 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe. 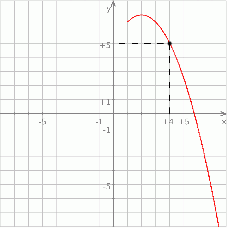
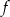 przecina oś
przecina oś 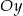 w punkcie
w punkcie 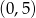 .
. 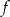 przyjmuje wartość 2.
przyjmuje wartość 2. 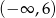 .
. 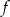 ma dwa miejsca zerowe, należące do przedziału
ma dwa miejsca zerowe, należące do przedziału 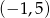 .
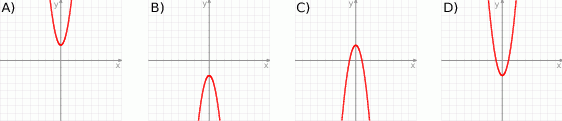
. 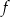 określonej wzorem
określonej wzorem 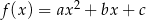 .
. 
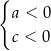
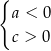
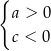
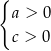
 określonej wzorem
określonej wzorem 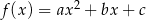 .
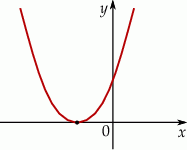
. 
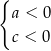
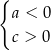
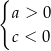
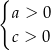
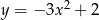 ?
? 
 ?
? 
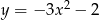 ?
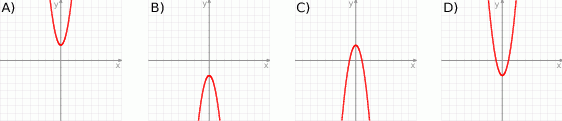
? 
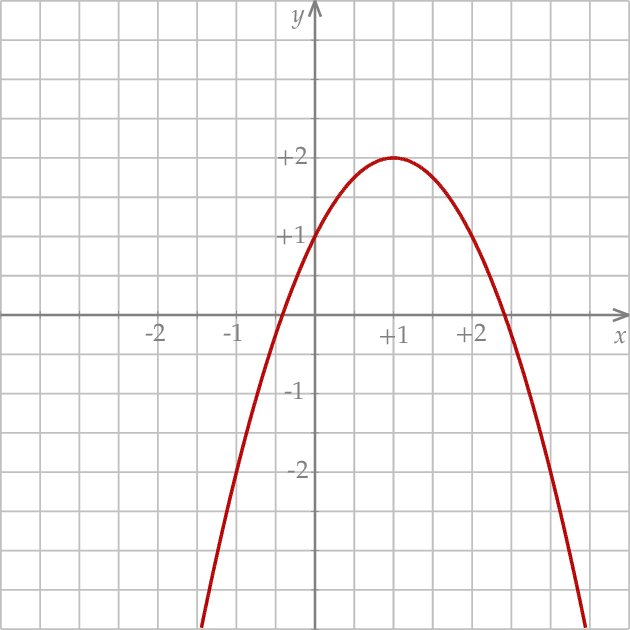
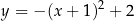
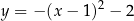
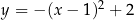
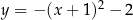
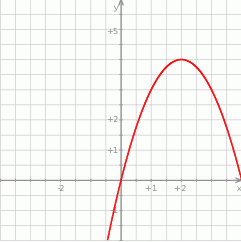
 , która jest wykresem funkcji kwadratowej
, która jest wykresem funkcji kwadratowej 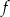 .
. 
 może być opisana wzorem
może być opisana wzorem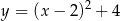
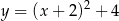
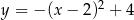
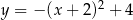
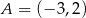 , która jest wykresem funkcji kwadratowej
, która jest wykresem funkcji kwadratowej 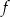 .
. 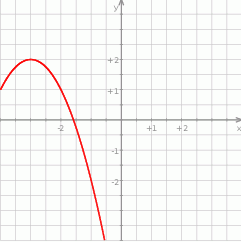
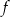 może być opisana wzorem
może być opisana wzorem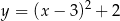
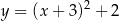
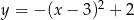
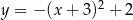
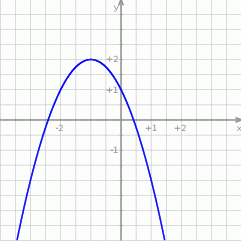
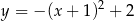
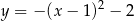
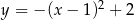
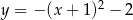
 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 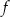 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite. 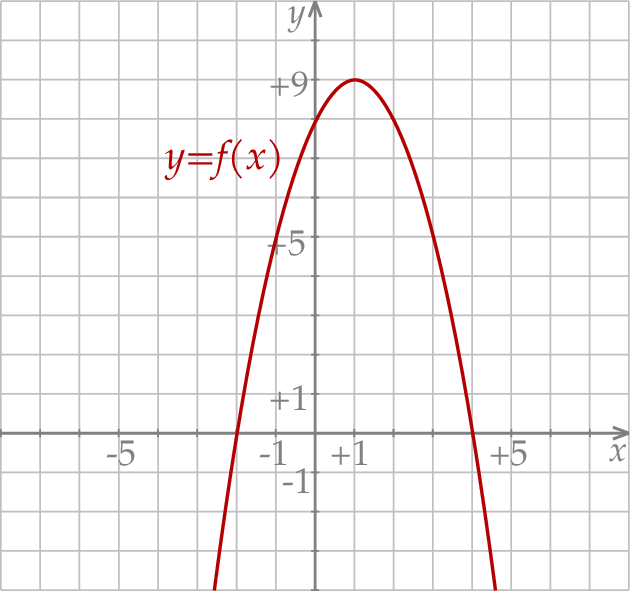
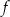 jest określona wzorem
jest określona wzorem 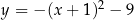
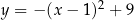
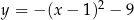
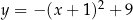
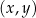 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 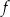 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osią 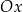 układu współrzędnych mają obie współrzędne całkowite.
układu współrzędnych mają obie współrzędne całkowite. 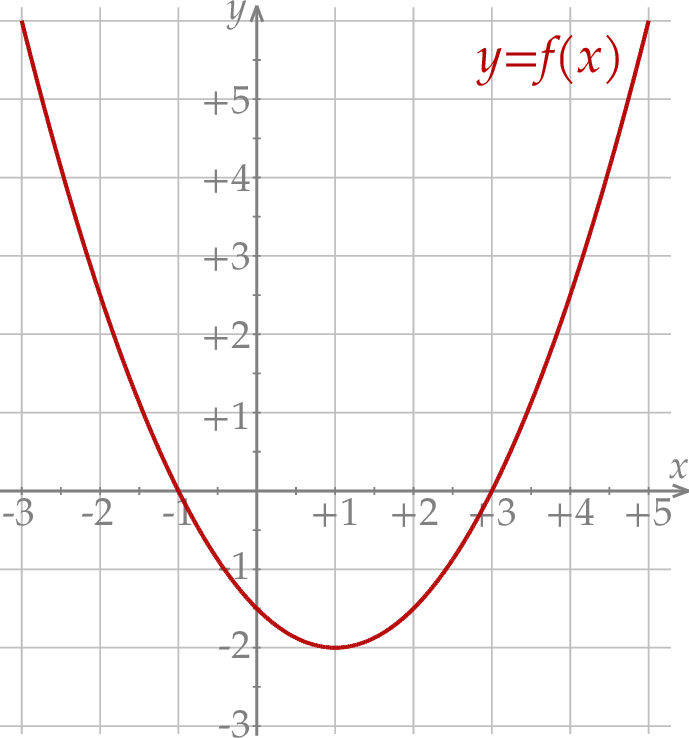
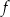 jest określona wzorem
jest określona wzorem 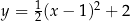
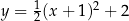
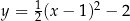
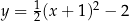
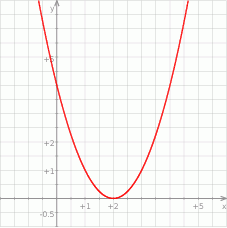
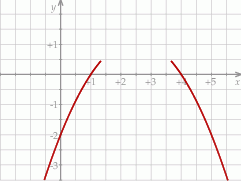
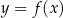 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 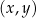 na rysunku poniżej.
na rysunku poniżej. 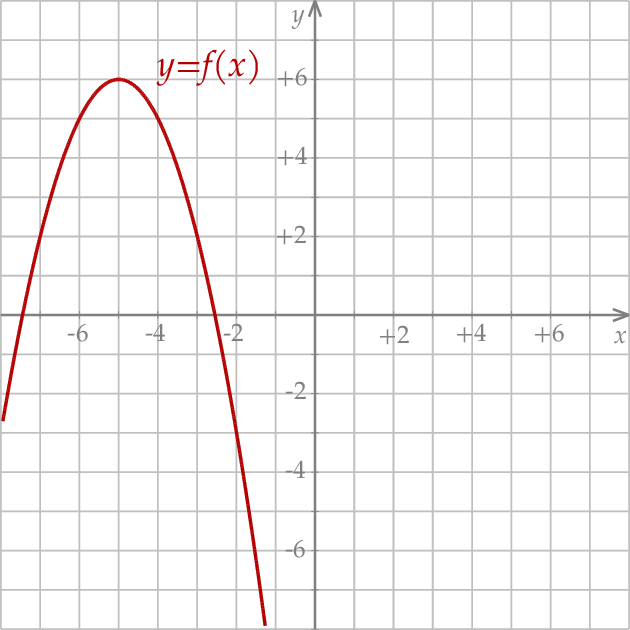
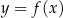 jest określona wzorem
jest określona wzorem 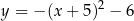
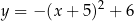
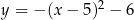
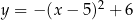
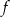 .
. 
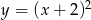
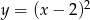
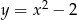
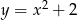
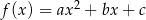 , której miejsca zerowe to:
, której miejsca zerowe to: 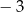 i 2. Do wykresu tego należy punkt
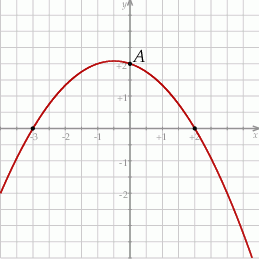
i 2. Do wykresu tego należy punkt 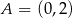 .
. 
 we wzorze funkcji
we wzorze funkcji 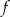 jest równy
jest równy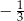
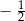
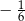
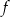 jest określona wzorem
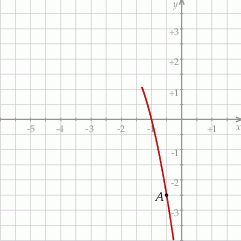
jest określona wzorem 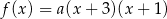 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 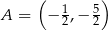 .
. 
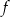 w przedziale
w przedziale 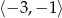 jest równa
jest równa 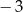
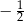
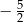
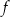 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 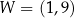 . Liczby
. Liczby 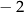 i 4 to miejsca zerowe funkcji
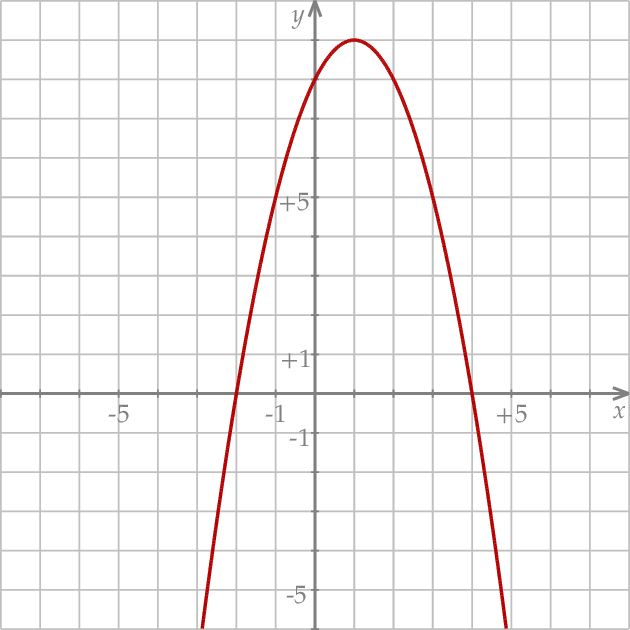
i 4 to miejsca zerowe funkcji 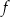 .
. 
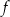 w przedziale
w przedziale 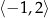 jest równa
jest równa 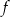 jest określona wzorem
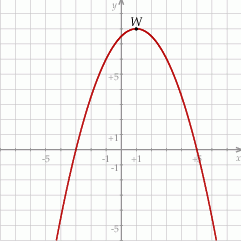
jest określona wzorem 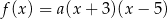 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 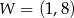 .
. 
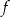 w przedziale
w przedziale 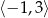 jest równa
jest równa 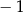
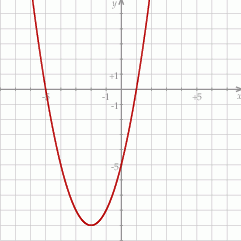
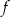 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 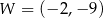 . Liczby
. Liczby 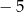 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 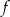 .
. 
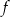 w przedziale
w przedziale 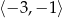 jest równa
jest równa 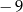
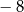
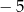
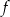 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 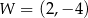 . Liczby 0 i 4 to miejsca zerowe funkcji
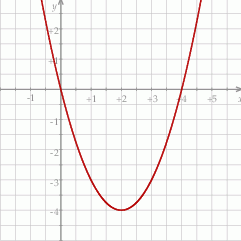
. Liczby 0 i 4 to miejsca zerowe funkcji 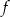 .
. 
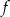 w przedziale
w przedziale 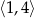 jest równa
jest równa 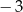
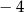
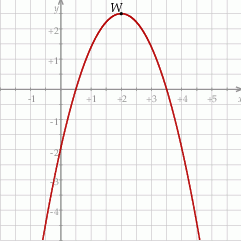
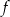 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 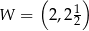 . Liczby
. Liczby 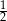 i
i 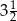 to miejsca zerowe funkcji
to miejsca zerowe funkcji 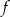 .
. 
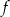 w przedziale
w przedziale 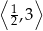 jest równa
jest równa 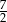
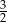

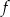 jest określona wzorem
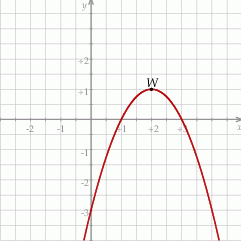
jest określona wzorem 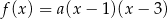 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 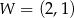 .
. 
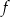 w przedziale
w przedziale 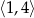 jest równa
jest równa 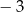
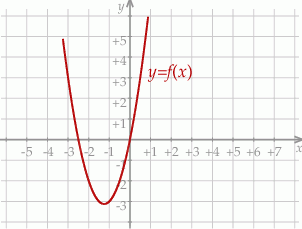
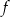 określonej wzorem
określonej wzorem 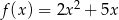 .
. 
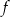 jest prosta o równaniu
jest prosta o równaniu 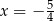
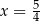
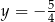
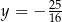
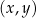 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 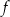 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite. 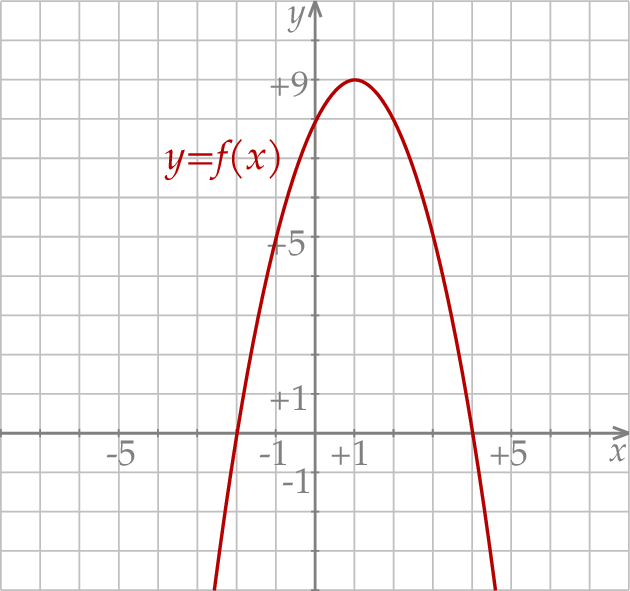
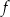 prawdziwa jest równość
prawdziwa jest równość 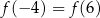
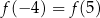
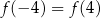
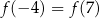
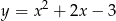 . Wskaż ten rysunek.
. Wskaż ten rysunek. 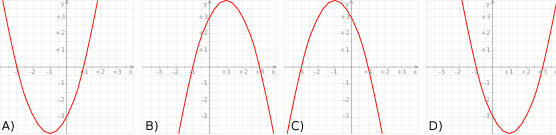
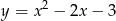 . Wskaż ten rysunek.
. Wskaż ten rysunek. 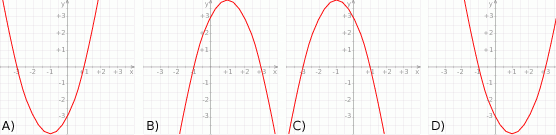
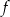 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 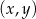 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 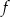 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 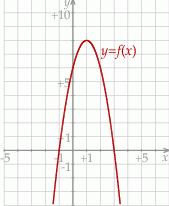
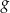 jest określona za pomocą funkcji
jest określona za pomocą funkcji 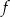 następująco:
następująco: 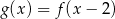 . Wykres funkcji
. Wykres funkcji 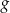 przedstawiono na rysunku
przedstawiono na rysunku 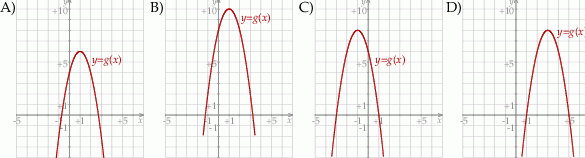
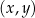 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 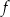 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 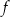 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 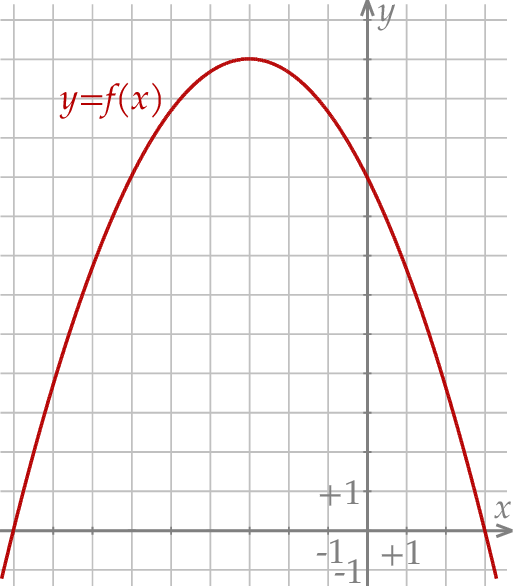
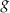 jest określona za pomocą funkcji
jest określona za pomocą funkcji 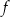 następująco:
następująco: 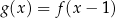 . Fragment wykresu funkcji
. Fragment wykresu funkcji 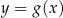 przedstawiono na rysunku
przedstawiono na rysunku 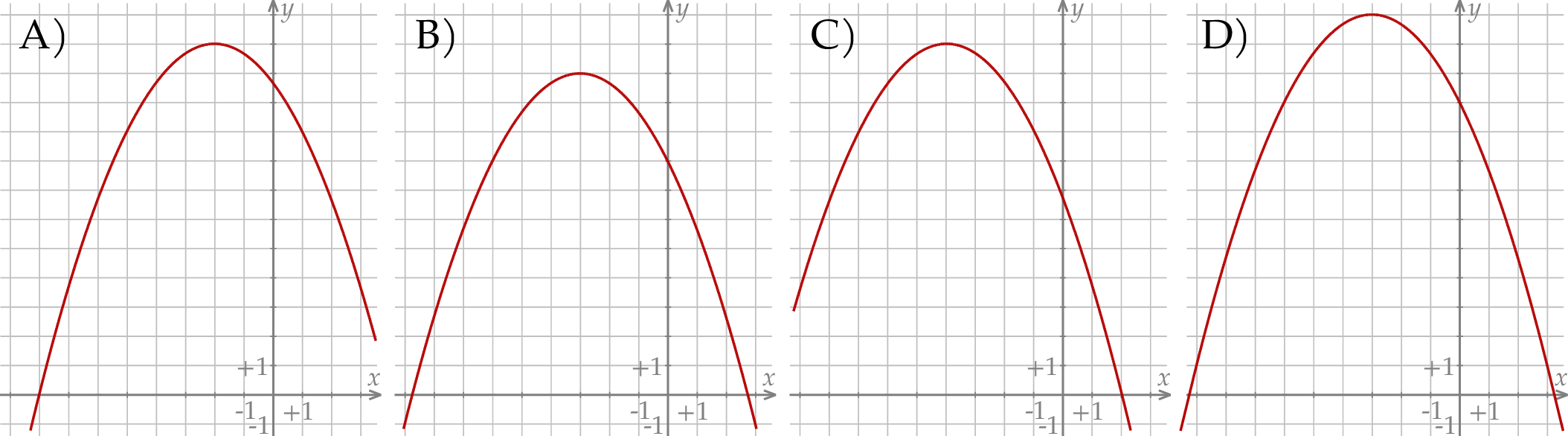
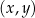 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 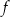 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 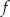 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 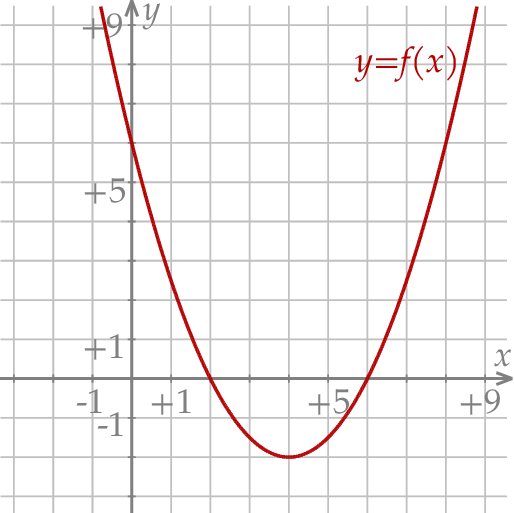
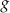 jest określona za pomocą funkcji
jest określona za pomocą funkcji 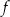 następująco:
następująco: 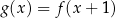 . Fragment wykresu funkcji
. Fragment wykresu funkcji 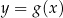 przedstawiono na rysunku
przedstawiono na rysunku 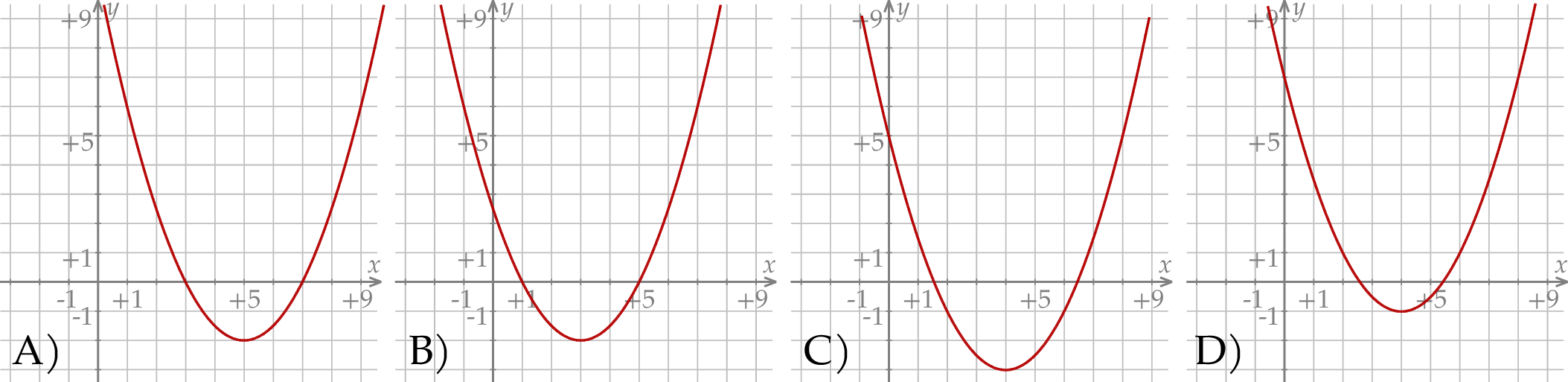
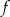 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 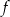 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite. 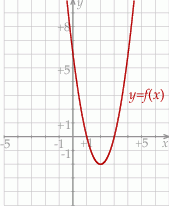
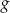 jest określona za pomocą funkcji
jest określona za pomocą funkcji 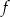 następująco:
następująco: 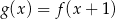 . Wykres funkcji
. Wykres funkcji 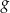 przedstawiono na rysunku
przedstawiono na rysunku 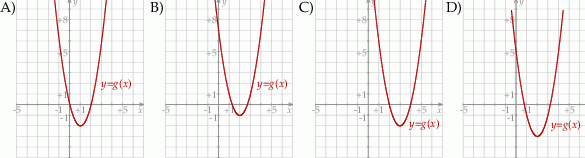
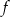 . Osią symetrii paraboli jest prosta o równaniu
. Osią symetrii paraboli jest prosta o równaniu 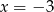 .
. 
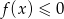 jest zbiór
jest zbiór 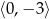
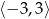
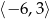
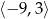
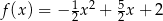
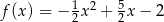
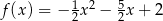
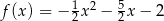
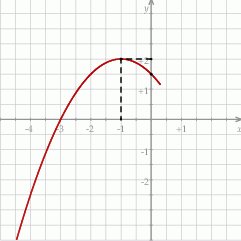
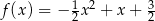
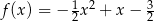
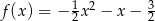
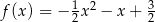
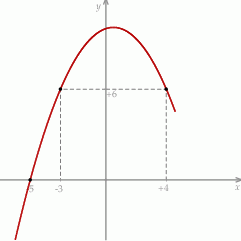
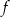 , określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty
, określonej dla wszystkich liczb rzeczywistych. Do tego wykresu należą punkty 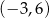 i
i 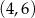 , a liczba
, a liczba 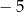 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 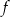 .
. 
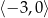 , to
, to 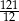
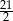
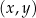 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 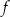 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite. 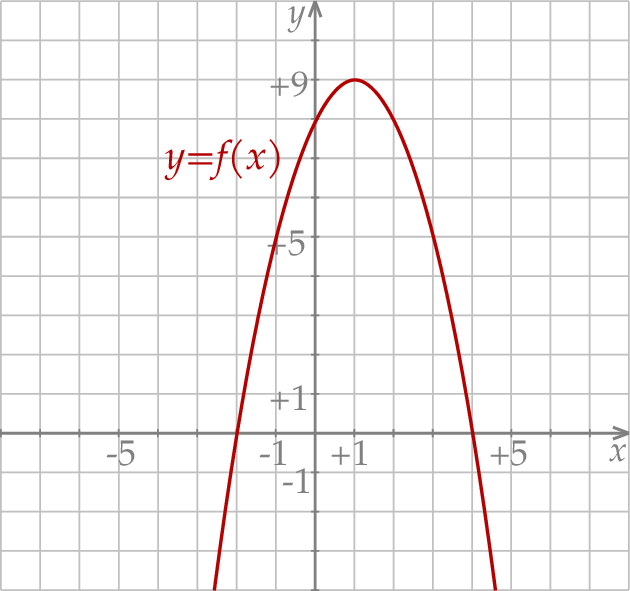
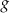 jest określona za pomocą funkcji
jest określona za pomocą funkcji 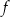 następująco:
następująco: 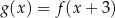 . Fragment wykresu funkcji
. Fragment wykresu funkcji 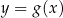 przedstawiono na rysunku
przedstawiono na rysunku 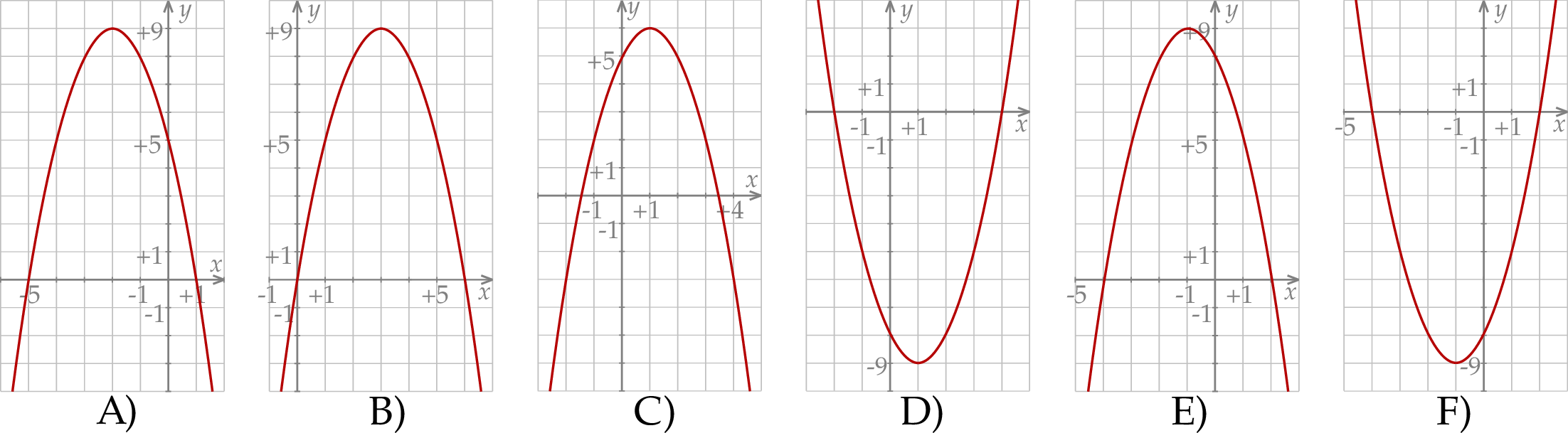
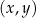 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 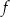 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite. 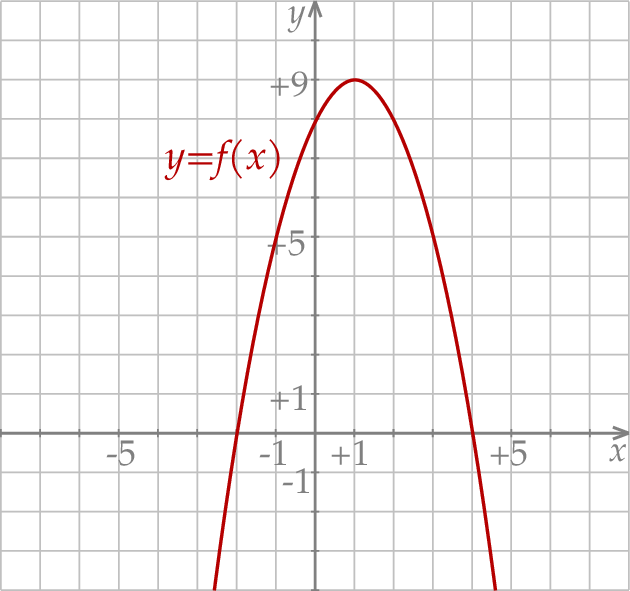
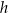 jest określona za pomocą funkcji
jest określona za pomocą funkcji 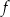 następująco:
następująco: 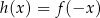 . Fragment wykresu funkcji
. Fragment wykresu funkcji 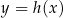 przedstawiono na rysunku
przedstawiono na rysunku 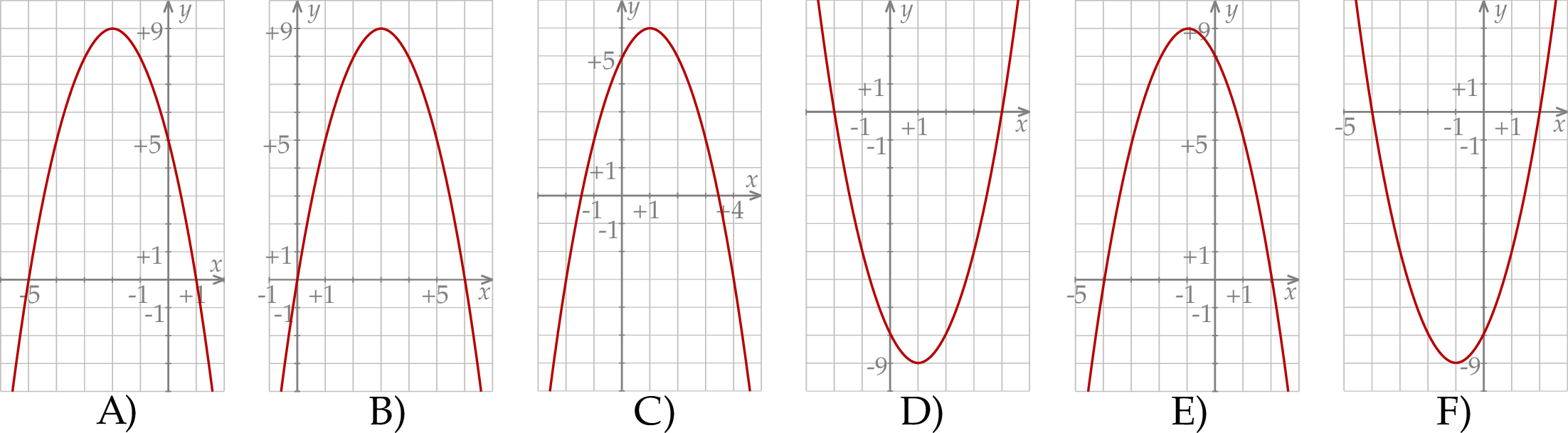
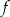 określonej wzorem
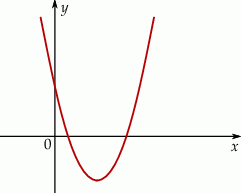
określonej wzorem 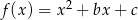 .
. 
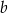 i
i  spełniają warunki:
spełniają warunki: 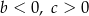
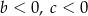
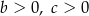
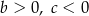
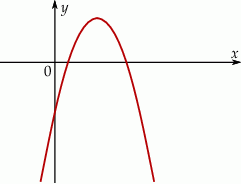
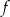 określonej wzorem
określonej wzorem 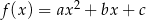 .
. 
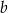 i
i  spełniają warunki:
spełniają warunki: 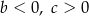
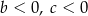
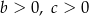
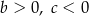
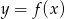 jest rozłączny z przedziałem
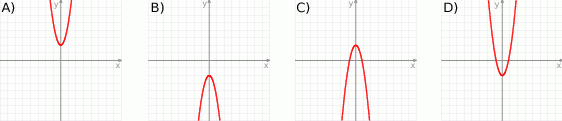
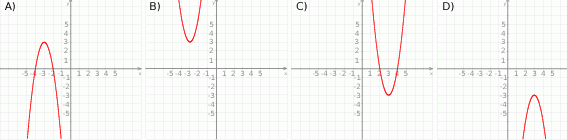
jest rozłączny z przedziałem 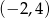 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 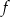 ?
? 
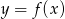 jest rozłączny z przedziałem
jest rozłączny z przedziałem 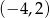 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 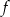 ?
?