Niech 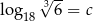 . Wykaż, że
. Wykaż, że 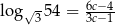 .
.
/Szkoła średnia/Liczby/Logarytmy/Tożsamości
Udowodnij, że jeśli liczby dodatnie  i
i 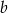 spełniają warunek
spełniają warunek 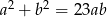 , to
, to 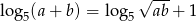 .
.
Wykaż, że jeżeli 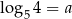 oraz
oraz 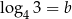 , to
, to 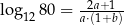 .
.
Udowodnij, że dla 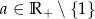 oraz
oraz 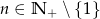 spełniona jest równość:
spełniona jest równość:
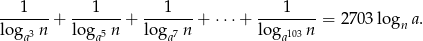
Wykaż, że 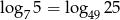 .
.
Niech 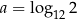 . Wykaż, że
. Wykaż, że 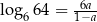 .
.
Niech 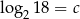 . Wykaż, że
. Wykaż, że 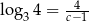 .
.
Niech 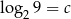 . Wykaż, że
. Wykaż, że 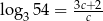 .
.
Wykaż, że jeżeli 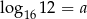 , to
, to 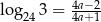 .
.
Niech 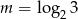 . Wykaż, że
. Wykaż, że 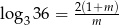 .
.
Niech 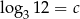 . Wykaż, że
. Wykaż, że 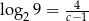 .
.
Niech 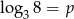 . Wykaż, że
. Wykaż, że 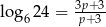 .
.
Niech 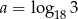 . Wykaż, że
. Wykaż, że 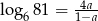 .
.
Niech 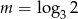 . Wykaż, że
. Wykaż, że 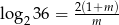 .
.
Udowodnij, że
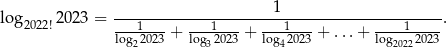
Wykaż, że jeżeli 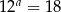 , to
, to 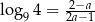 .
.
Dodatnie liczby rzeczywiste  i
i 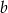 takie, że
takie, że 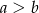 , spełniają warunek
, spełniają warunek
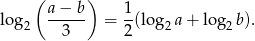
Wykaż, że dla liczb  i
i 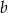 prawdziwa jest równość
prawdziwa jest równość 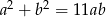 .
.
Korzystając ze wzoru
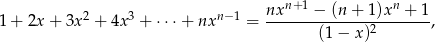
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 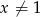 , wykaż, że
, wykaż, że
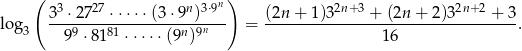
Wykaż, że dla liczb spełniających odpowiednie założenia (podaj te założenia) prawdziwy jest wzór: 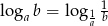 .
.
Wykaż, że jeżeli 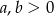 i
i 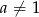 , to dla dowolnej liczby całkowitej dodatniej
, to dla dowolnej liczby całkowitej dodatniej  prawdziwy jest wzór
prawdziwy jest wzór
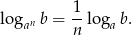
Niech 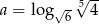 . Wykaż, że
. Wykaż, że 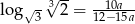 .
.
Wykaż, że dla 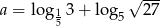 i
i 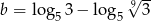 prawdziwa jest równość
prawdziwa jest równość 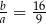 .
.
Wykaż, że dla każdej dodatniej i różnej od jedności liczby  i dla każdej dodatniej i różnej od jedności liczby
i dla każdej dodatniej i różnej od jedności liczby 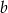 spełniona jest równość
spełniona jest równość
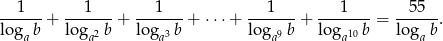
Dane są liczby rzeczywiste  i
i 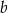 takie, że
takie, że 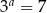 i
i 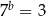 . Wykaż, ze
. Wykaż, ze
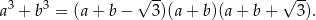
Liczby rzeczywiste 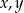 spełniają warunki:
spełniają warunki: 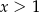 ,
, 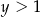 oraz
oraz 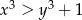 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
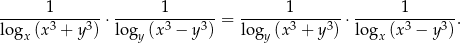
Udowodnij, że liczby 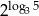 i
i 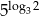 są równe.
są równe.
Uzasadnij, że 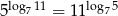 .
.
Wykaż, że dla każdej dodatniej liczby rzeczywistej  różnej od 1 oraz dla każdej dodatniej liczby rzeczywistej
różnej od 1 oraz dla każdej dodatniej liczby rzeczywistej 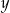 różnej od 1 prawdziwa jest równość
różnej od 1 prawdziwa jest równość
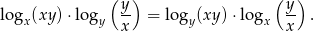
Udowodnij, że jeżeli 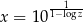 i
i 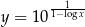 , to
, to 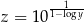 .
.
Wiadomo, że 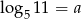 . Wykaż, że
. Wykaż, że 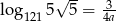 .
.

