Z liczb ośmioelementowego zbioru 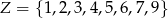 tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
tworzymy ośmiowyrazowy ciąg, którego wyrazy się nie powtarzają. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Własności cyfr
Ze zbioru liczb dwucyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest dodatnią liczbą złożoną?
Ze zbioru liczb 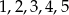 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 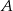 – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Ze zbioru liczb 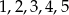 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 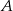 – otrzymana liczba jest większa od 324.
– otrzymana liczba jest większa od 324.
Ze zbioru 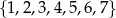 losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
losujemy kolejno, bez zwracania trzy cyfry i tworzymy liczbę trzycyfrową: pierwsza wylosowana cyfra jest cyfrą setek, druga – cyfrą dziesiątek, a trzecia – cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że otrzymana liczba ma następującą własność: różnica między największą i najmniejszą cyfrą tej liczby jest nie większa niż 3.
Spośród wszystkich czterocyfrowych całkowitych liczb dodatnich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba będzie parzysta, a w jej zapisie dziesiętnym wystąpią dokładnie jedna cyfra 2 i dokładnie jedna cyfra 3.
Spośród wszystkich liczb naturalnych sześciocyfrowych, których wszystkie cyfry należą do zbioru 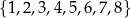 , losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
, losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
Ze zbioru liczb 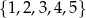 losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 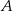 – otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
– otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
Spośród cyfr 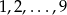 losujemy bez zwracania dwie i tworzymy z nich liczbę dwucyfrową, której cyfrą dziesiątek jest pierwsza z wylosowanych cyfr. Oblicz prawdopodobieństwo że otrzymana liczba jest parzysta.
losujemy bez zwracania dwie i tworzymy z nich liczbę dwucyfrową, której cyfrą dziesiątek jest pierwsza z wylosowanych cyfr. Oblicz prawdopodobieństwo że otrzymana liczba jest parzysta.
Z cyfr 0, 1, 2, 3, 4 układamy wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Ze zbioru takich liczb losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 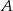 – wybrana liczba trzycyfrowa ma tę własność, że cyfry: setek, dziesiątek oraz jedności (w podanej kolejności) tworzą ciąg arytmetyczny.
– wybrana liczba trzycyfrowa ma tę własność, że cyfry: setek, dziesiątek oraz jedności (w podanej kolejności) tworzą ciąg arytmetyczny.
Oblicz prawdopodobieństwo wylosowania spośród wszystkich liczb trzycyfrowych liczby, której suma cyfr jest równa 2?
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba całkowita dodatnia mniejsza od 10000 jest czterocyfrowa.
Zbiór 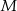 tworzą wszystkie liczby naturalne dwucyfrowe, w zapisie których występują dwie różne cyfry spośród: 1, 2, 3, 4, 5. Ze zbioru
tworzą wszystkie liczby naturalne dwucyfrowe, w zapisie których występują dwie różne cyfry spośród: 1, 2, 3, 4, 5. Ze zbioru 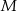 losujemy jedną liczbę, przy czym każda liczba z tego zbioru może być wylosowana z tym samym prawdopodobieństwem. Oblicz prawdopodobieństwo, że wylosujemy liczbę większą od 20, w której cyfra dziesiątek jest mniejsza od cyfry jedności.
losujemy jedną liczbę, przy czym każda liczba z tego zbioru może być wylosowana z tym samym prawdopodobieństwem. Oblicz prawdopodobieństwo, że wylosujemy liczbę większą od 20, w której cyfra dziesiątek jest mniejsza od cyfry jedności.
Ze zbioru liczb trzycyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest liczbą parzystą?
Ze zbioru liczb trzycyfrowych, które nie mają dwóch takich samych cyfr losujemy jedną liczbę. Jakie jest prawdopodobieństwo otrzymania liczby, której iloczyn cyfr jest liczbą niezerową podzielną przez 7?
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 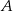 polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 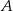 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 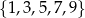 , i jednocześnie cyfrę jedności, która należy do zbioru
, i jednocześnie cyfrę jedności, która należy do zbioru 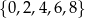 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 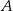 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Z cyfr 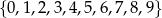 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
Z cyfr 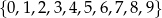 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
Z cyfr 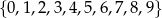 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.
Ze zbioru wszystkich liczb naturalnych ośmiocyfrowych, w których zapisie dziesiętnym występują tylko cyfry ze zbioru 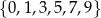 , losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
, losujemy jedną. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma cyfr wylosowanej liczby jest równa 3.
Spośród liczb naturalnych ośmiocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby o sumie cyfr równej 4, jeżeli wiadomo, że żadna cyfra wylosowanej liczby nie jest równa 2, 3, 6 ani 8.
Spośród cyfr 1, 2, 3, 4, 5, 6 losujemy kolejno dwa razy po jednej cyfrze ze zwracaniem. Tworzymy liczbę dwucyfrową w ten sposób, że pierwsza z wylosowanych cyfr jest cyfrą dziesiątek, a druga cyfrą jedności tej liczby. Oblicz prawdopodobieństwo utworzenia liczby większej od 52.

