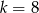Jednym z rozwiązań równania 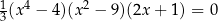 jest liczba
jest liczba
A) 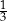 B)
B) 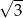 C)
C) 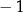 D)
D) 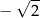
/Szkoła średnia/Zadania testowe/Równania/Wielomianowe/Wyższego stopnia
Dany jest wielomian 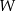 określony wzorem
określony wzorem 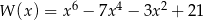 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 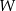 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 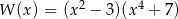 B)
B) 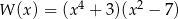
C) 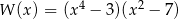 D)
D) 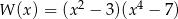
Liczba ujemnych pierwiastków równania 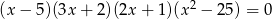 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 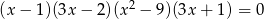 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 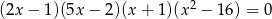 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Suma wszystkich rozwiązań równania 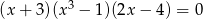 jest równa
jest równa
A) 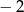 B)
B) 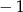 C) 0 D) 2
C) 0 D) 2
Iloczyn wszystkich rozwiązań równania 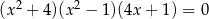 jest równy
jest równy
A) 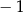 B)
B) 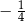 C)
C) 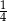 D) 1
D) 1
Funkcja 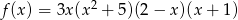 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Funkcja 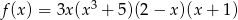 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Równanie 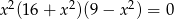 ma dokładnie
ma dokładnie
A) pięć rozwiązań: 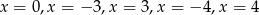
B) trzy rozwiązania: 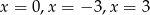
C) dwa rozwiązania: 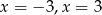
D) jedno rozwiązanie: 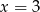
Rozwiązaniami równania 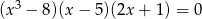 są liczby
są liczby
A) 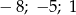 B)
B) 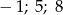 C)
C) 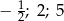 D)
D) 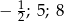
Rozwiązaniami równania 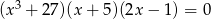 są liczby
są liczby
A) 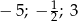 B)
B) 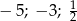 C)
C) 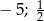 D)
D) 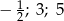
Spośród liczb, które są rozwiązaniami równania 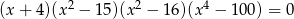 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest liczbą
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest liczbą
A) ujemną B) całkowitą C) niewymierną D) większą od 100
Iloczyn wszystkich rzeczywistych pierwiastków równania
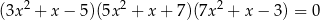
jest równy
A) 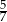 B) 1 C)
B) 1 C) 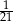 D)
D) 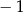
Liczba niewymiernych rozwiązań równania 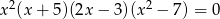 jest równa
jest równa
A) 0 B) 1 C) 5 D) 2
Liczba niewymiernych rozwiązań równania 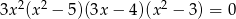 jest równa
jest równa
A) 1 B) 2 C) 4 D) 5
Liczba rozwiązań równania 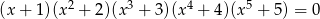 jest równa
jest równa
A) 9 B) 5 C) 3 D) 1
Równanie 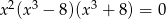 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Równanie 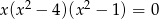 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Równanie 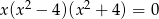 z niewiadomą
z niewiadomą 
A) nie ma rozwiązań w zbiorze liczb rzeczywistych.
B) ma dokładnie dwa rozwiązania w zbiorze liczb rzeczywistych.
C) ma dokładnie trzy rozwiązania w zbiorze liczb rzeczywistych.
D) ma dokładnie pięć rozwiązań w zbiorze liczb rzeczywistych.
Spośród liczb, które są rozwiązaniami równania 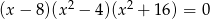 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A) 12 B) 10 C) 6 D) 4
Spośród liczb, które są rozwiązaniami równania 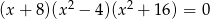 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A) 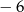 B)
B) 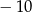 C) 6 D) 24
C) 6 D) 24
Liczba pierwiastków całkowitych wielomianu 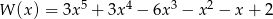 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Suma rozwiązań równania 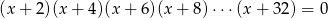 jest równa
jest równa
A) 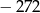 B)
B) 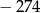 C)
C) 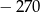 D)
D) 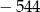
Liczba rzeczywistych pierwiastków równania 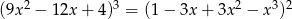 jest równa
jest równa
A) 4 B) 2 C) 1 D) 0
Suma pierwiastków wielomianu 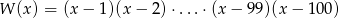 jest równa
jest równa
A) 100 B) 10000 C) 10100 D) 5050
Suma pierwiastków wielomianu 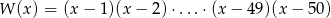 jest równa
jest równa
A) 1275 B) 2550 C) 5100 D) 5050
Suma pierwiastków wielomianu 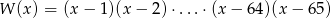 jest równa
jest równa
A) 4290 B) 2145 C) 2080 D) 8580
Liczba rzeczywistych rozwiązań równania 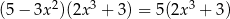 jest równa
jest równa
A) 5 B) 3 C) 2 D) 4
Liczba -1 jest miejscem zerowym wielomianu 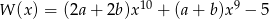 i
i 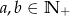 . Wynika stąd, że
. Wynika stąd, że
A)  i
i 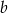 to liczby parzyste
to liczby parzyste
B)  i
i 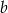 to liczby nieparzyste
to liczby nieparzyste
C) jedna z liczb 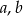 jest parzysta, a druga nieparzysta
jest parzysta, a druga nieparzysta
D) 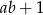 jest liczbą parzystą
jest liczbą parzystą
Liczba -1 jest miejscem zerowym wielomianu 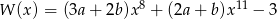 i
i 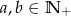 . Wynika stąd, że
. Wynika stąd, że
A)  i
i 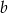 to liczby parzyste
to liczby parzyste
B) jedna z liczb 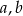 jest parzysta, a druga nieparzysta
jest parzysta, a druga nieparzysta
C)  i
i 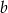 to liczby nieparzyste
to liczby nieparzyste
D) 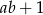 jest liczbą parzystą
jest liczbą parzystą
Liczba -1 jest miejscem zerowym wielomianu 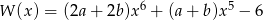 i
i 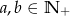 . Wynika stąd, że
. Wynika stąd, że
A)  i
i 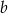 są liczbami o tej samej parzystości
są liczbami o tej samej parzystości
B)  i
i 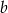 to liczby nieparzyste
to liczby nieparzyste
C) jedna z liczb 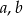 jest parzysta, a druga nieparzysta
jest parzysta, a druga nieparzysta
D) 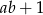 jest liczbą parzystą
jest liczbą parzystą
Równanie 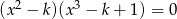 nie ma rozwiązań niewymiernych. Liczba
nie ma rozwiązań niewymiernych. Liczba 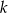 może być równa
może być równa
A) 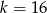 B)
B) 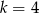 C)
C) 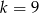 D)
D)