Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 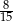 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 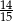 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej jest równe
A) 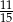 B)
B) 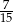 C)
C) 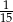 D)
D) 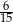
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo/Urna
Z szuflady zawierającej piłki w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej piłki czerwonej jest równe 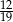 , a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej piłki zielonej jest równe 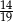 . Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie jednej piłki czerwonej jest równe
A) 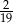 B)
B) 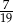 C)
C) 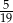 D)
D) 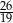
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 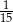 B)
B) 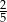 C)
C) 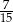 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 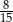 B)
B) 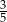 C)
C) 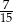 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 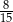 B)
B) 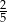 C)
C) 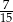 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 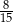 B)
B) 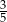 C)
C) 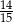 D)
D) 
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są jedna kula biała i sześć kul czarnych, w drugiej urnie są cztery kule białe i trzy kule czarne. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy kulę białą w tym doświadczeniu, jest równe
A) 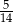 B)
B) 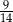 C)
C)  D)
D) 
W każdym z czterech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 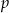 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z czterech wylosowanych kul będą niebieskie. Wtedy
A) 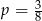 B)
B) 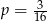 C)
C) 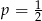 D)
D) 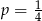
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie trzy razy w czterech losowaniach wyciągniemy kulę koloru białego, jest równe
A) 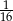 B)
B)  C)
C) 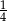 D)
D) 
W każdym z pięciu pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 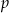 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z pięciu wylosowanych kul będą niebieskie. Wtedy
A) 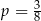 B)
B) 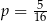 C)
C) 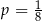 D)
D) 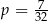
W pudełku znajdują się dwie kule: czarna i biała. Czterokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy w czterech losowaniach wyciągniemy kulę koloru czarnego, jest równe
A) 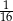 B)
B)  C)
C) 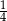 D)
D) 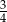
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była czarna. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z pierwszej z tych urn, jest równe
A) 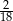 B)
B) 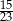 C)
C) 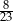 D)
D) 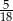
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była biała. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z drugiej z tych urn, jest równe
A) 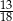 B)
B) 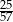 C)
C) 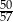 D)
D) 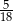
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli białej jest równe 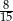 , a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli białej jest równe 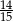 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych jest równe
A) 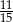 B)
B) 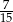 C)
C) 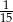 D)
D) 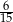
Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo wylosowania co najmniej jednej kuli niebieskiej jest równe 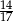 , a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe
, a prawdopodobieństwo wybrania co najwyżej jednej kuli niebieskiej jest równe 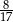 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul niebieskich jest równe
A) 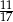 B)
B) 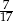 C)
C) 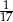 D)
D) 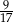
Z pudełka zwierającego losy wygrywające i przegrywające wybieramy dwa losy. Prawdopodobieństwo wylosowania co najmniej jednego losu wygrywającego jest równe 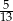 , a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe
, a prawdopodobieństwo wybrania co najwyżej jednego losu wygrywającego jest równe 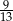 . Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch losów wygrywających jest równe
A) 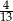 B)
B) 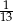 C)
C) 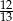 D)
D) 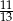
W pudełku znajdują się dwie kule: niebieska i czerwona. Dziewięciokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie osiem z wylosowanych kul jest tego samego koloru jest równe
A) 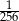 B)
B) 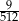 C)
C) 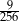 D)
D) 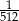
W pudełku znajdują się dwie kule: niebieska i czerwona. Ośmiokrotnie losujemy ze zwracaniem jedną kulę z tego pudełka. Prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie siedem z wylosowanych kul jest tego samego koloru jest równe
A) 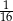 B)
B) 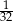 C)
C) 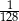 D)
D) 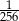
W pudełku znajdują się wyłącznie kule białe i czarne. Kul czarnych jest 18. Z tego pudełka w sposób losowy wyciągamy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kulę czarną, jest równe  . Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
. Liczba kul białych w pudełku, przed wyciągnięciem jednej kuli, była równa
A) 9 B) 12 C) 15 D) 30
W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul białych do liczby kul czarnych jest równy 3:4. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)  B)
B)  C)
C) 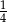 D)
D) 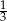
W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul czarnych do liczby kul białych jest równy 4:5. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)  B)
B)  C)
C) 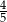 D)
D) 
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 3:4. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 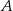 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 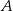 jest równe
jest równe
A) 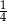 B)
B) 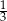 C)
C) 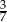 D)
D) 
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4:5. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 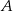 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 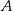 jest równe
jest równe
A) 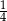 B)
B) 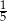 C)
C) 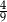 D)
D) 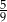
W pojemniku są wyłącznie kule białe i czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 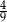 B)
B)  C)
C) 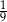 D)
D) 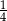
W woreczku są tylko koraliki białe i czerwone. Białych koralików jest cztery razy więcej niż czerwonych. Losujemy jeden koralik. Prawdopodobieństwo, że wylosujemy biały koralik, jest równe
A) 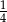 B)
B) 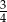 C)
C) 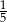 D)
D) 
W pudełku są 4 kule białe i  kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe
kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe  , gdy
, gdy
A) 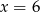 B)
B) 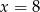 C)
C) 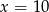 D)
D) 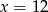
Z pudełka, w którym jest tylko 6 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe 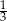 . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 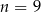 B)
B) 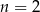 C)
C) 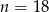 D)
D) 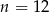
Z pudełka, w którym jest tylko 8 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe  . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 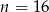 B)
B) 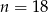 C)
C) 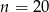 D)
D) 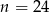
W pudełku jest 5 kul czerwonych i  kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe
kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe  , gdy
, gdy
A) 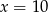 B)
B) 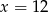 C)
C) 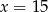 D)
D) 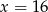
W pudełku jest 40 kul. Wśród nich jest 35 kul białych, a pozostałe to kule czerwone. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę czerwoną, jest równe
A)  B)
B) 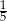 C)
C) 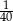 D)
D) 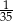
W pudełku jest 60 kul. Wśród nich jest 27 kul białych, 18 kul niebieskich, a pozostałe to kule żółte. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę, która nie jest niebieska, jest równe
A) 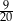 B)
B) 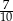 C)
C) 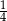 D)
D) 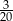
W pokoju w kilkunastu ponumerowanych workach znajdują się kolorowe piłki. Miłosz z zamkniętymi oczami wybiera losowo jeden z tych worków, a potem z wybranego worka wybiera jedną piłkę. Prawdopodobieństwo wybrania białej piłki z worka numer 1 jest równe 0,3, a prawdopodobieństwo, że Miłosz wybierze worek numer 1 jest równe 0,4. Jakie jest prawdopodobieństwo tego, że Miłosz wybierze worek numer 1 i z tego worka wyjmie piłkę, która nie jest biała?
A) 0,7 B) 0,9 C) 0,12 D) 0,28
W urnie zawierającej kule białe i czarne jest 60 kul. Losujemy jedną kulę. Jeśli prawdopodobieństwo wylosowania kuli białej jest równe  , to kul czarnych w tej urnie jest
, to kul czarnych w tej urnie jest
A) 30 B) 24 C) 20 D) 36
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B) 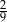 C)
C)  D)
D) 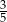
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej lub białej jest równe
A)  B)
B) 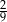 C)
C) 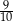 D)
D) 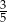
W pojemniku są wyłącznie kule białe, czerwone, niebieskie i żółte. Kul białych jest tyle samo co kul niebieskich, kul czerwonych jest dwa razy więcej niż kul żółtych, a stosunek liczby kul żółtych do liczby kul niebieskich jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli, która nie jest czerwona jest równe
A) 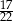 B)
B) 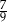 C)
C) 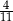 D)
D) 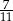
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 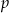 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie z trzech wylosowanych kul będą czerwone. Wtedy
A) 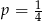 B)
B) 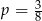 C)
C) 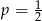 D)
D) 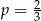
W każdym z trzech pojemników znajduje się para kul, z których jedna jest czerwona, a druga – niebieska. Z każdego pojemnika losujemy jedną kulę. Niech 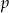 oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
oznacza prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie jedna z trzech wylosowanych kul będzie czerwona. Wtedy
A) 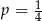 B)
B) 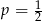 C)
C) 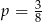 D)
D) 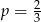
W pudełku znajdują się kule w trzech kolorach: czerwone, białe i niebieskie, przy czym prawdopodobieństwo wylosowania kuli czerwonej jest dwa razy mniejsze od prawdopodobieństwa wylosowania kuli białej, a prawdopodobieństwo wylosowania kuli niebieskiej jest trzy razy mniejsze od prawdopodobieństwa wylosowania kuli czerwonej. Prawdopodobieństwo wylosowania kuli białej jest równe
A)  B)
B)  C)
C) 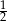 D)
D) 
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czerwonej i dwa razy mniejsze niż wylosowanie kuli białej. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest równe
A) 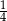 B)
B) 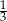 C)
C)  D)
D) 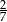
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli czerwonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli białej i dwa razy mniejsze niż wylosowanie kuli zielonej. Prawdopodobieństwo wylosowania z pudełka kuli białej jest równe
A) 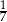 B)
B) 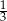 C)
C)  D)
D)