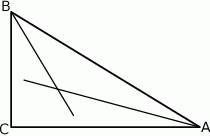
W trójkącie prostokątnym 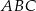 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 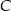 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 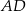 i
i 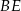 . Udowodnij, że
. Udowodnij, że 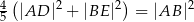 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...
Punkty 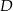 i
i 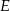 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 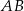 trójkąta prostokątnego
trójkąta prostokątnego 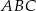 , że
, że 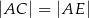 i
i 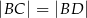 . Wykaż, że
. Wykaż, że 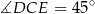 .
.
Dany jest trójkąt prostokątny 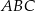 , w którym
, w którym 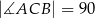 i
i 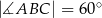 . Niech
. Niech 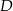 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 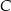 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 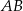 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 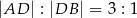 .
.
Na przeciwprostokątnej 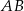 trójkąta prostokątnego
trójkąta prostokątnego 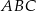 zbudowano kwadrat
zbudowano kwadrat 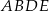 .
.
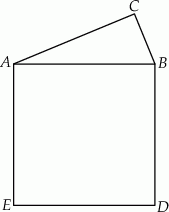
Stosunek pola trójkąta do pola kwadratu jest równy 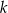 . Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa
. Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa 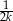 .
.
Przez środek 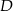 przyprostokątnej
przyprostokątnej 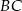 trójkąta prostokątnego
trójkąta prostokątnego 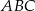 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 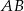 . Prosta ta przecina proste
. Prosta ta przecina proste 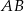 i
i 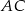 odpowiednio w punktach
odpowiednio w punktach 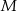 i
i 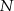 . Wykaż, że
. Wykaż, że 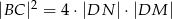 .
.
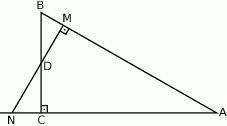
Przez środek 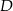 przyprostokątnej
przyprostokątnej 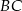 trójkąta prostokątnego
trójkąta prostokątnego 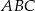 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 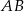 . Prosta ta przecina proste
. Prosta ta przecina proste 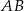 i
i 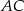 odpowiednio w punktach
odpowiednio w punktach 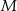 i
i 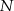 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 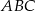 i
i 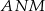 jest równa
jest równa 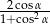 .
.
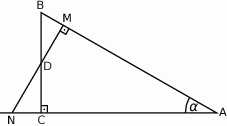
Na przyprostokątnych 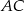 i
i 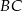 trójkąta prostokątnego
trójkąta prostokątnego 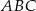 zbudowano trójkąty równoramienne
zbudowano trójkąty równoramienne 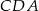 i
i 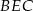 w ten sposób, że
w ten sposób, że 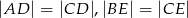 oraz punkty
oraz punkty 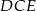 leżą na jednej prostej. Wykaż, że proste
leżą na jednej prostej. Wykaż, że proste 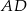 i
i 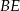 są równoległe.
są równoległe.
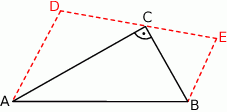
Uzasadnij, że przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu na nim opisanego.
W trójkącie prostokątnym 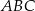 punkt
punkt 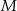 leży na przeciwprostokątnej
leży na przeciwprostokątnej 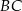 . Z punktu
. Z punktu 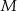 poprowadzono odcinki
poprowadzono odcinki 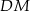 i
i 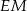 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 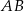 i
i 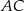 (rysunek).
(rysunek).
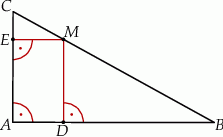
Udowodnij, że
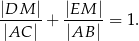
Trójkąt 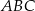 jest prostokątny. Z punktu
jest prostokątny. Z punktu 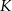 należącego do przeciwprostokątnej
należącego do przeciwprostokątnej 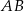 poprowadzono odcinki
poprowadzono odcinki 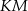 oraz
oraz 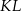 prostopadłe odpowiednio do przyprostokątnych
prostopadłe odpowiednio do przyprostokątnych 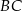 oraz
oraz 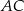 (rysunek).
(rysunek).
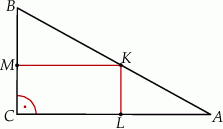
Wykaż, że
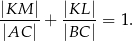
Na zewnątrz równoramiennego trójkąta prostokątnego zbudowano kwadraty – jeden na przyprostokątnej, a drugi na przeciwprostokątnej. Wykaż, że przeciwprostokątna dzieli odcinek łączący środki kwadratów na dwie równe części.
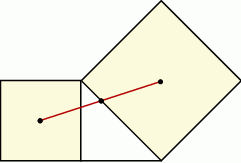
Przez środek 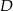 przyprostokątnej
przyprostokątnej 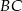 trójkąta prostokątnego
trójkąta prostokątnego 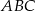 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 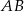 . Prosta ta przecina proste
. Prosta ta przecina proste 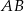 i
i 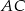 odpowiednio w punktach
odpowiednio w punktach 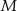 i
i 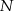 . Wykaż, że
. Wykaż, że 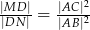 .
.
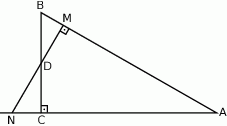
Wykaż, że jeżeli pole trójkąta prostokątnego jest równe 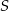 , to długość jego przeciwprostokątnej jest nie mniejsza niż
, to długość jego przeciwprostokątnej jest nie mniejsza niż 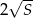 .
.
Dwusieczna kąta ostrego 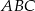 przecina przyprostokątną
przecina przyprostokątną 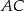 trójkąta prostokątnego
trójkąta prostokątnego 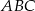 w punkcie
w punkcie 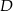 .
.
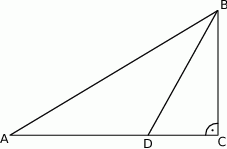
Udowodnij, że jeżeli 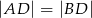 , to
, to 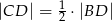 .
.
Dwusieczna kąta ostrego 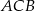 przecina przyprostokątną
przecina przyprostokątną 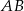 trójkąta prostokątnego
trójkąta prostokątnego 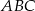 w punkcie
w punkcie  .
.
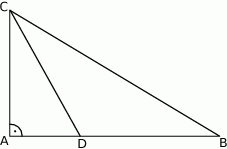
Udowodnij, że jeżeli 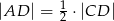 , to
, to 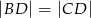 .
.
Dany jest trójkąt prostokątny, którego przyprostokątne mają długości  i
i 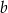 . Punkt
. Punkt 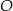 leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
leży na przeciwprostokątnej tego trójkąta i jest środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
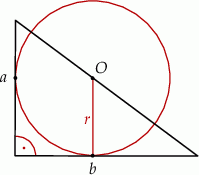
Wykaż, że promień  tego okręgu jest równy
tego okręgu jest równy 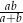 .
.
Uzasadnij, że trójkąty prostokątne 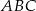 i
i 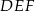 (patrz rysunek) są podobne.
(patrz rysunek) są podobne.
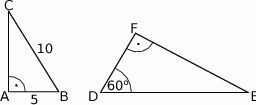
Uzasadnij, że trójkąty prostokątne 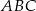 i
i 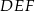 (patrz rysunek) są podobne.
(patrz rysunek) są podobne.
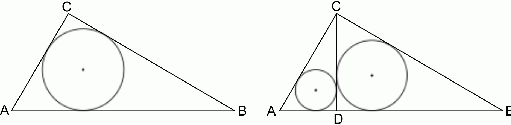
Dany jest trójkąt prostokątny 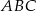 , w którym
, w którym 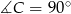 . W trójkącie tym poprowadzono wysokość
. W trójkącie tym poprowadzono wysokość 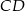 . Wykaż, że
. Wykaż, że 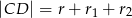 , gdzie
, gdzie 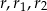 są odpowiednio długościami promieni okręgów wpisanych w trójkąty
są odpowiednio długościami promieni okręgów wpisanych w trójkąty 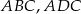 i
i  .
.
Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.
Dany jest trójkąt prostokątny o polu 6, w którym długość przeciwprostokątnej jest liczbą z przedziału 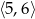 . Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału
. Wykaż, że suma długości przyprostokątnych tego trójkąta jest liczbą z przedziału 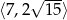 .
.
Uzasadnij, że jeżeli 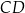 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 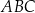 , w którym
, w którym 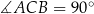 to
to 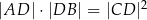 .
.

Wykaż, że jeżeli długości boków 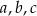 trójkąta prostokątnego są liczbami całkowitymi, to liczba
trójkąta prostokątnego są liczbami całkowitymi, to liczba 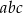 jest parzysta.
jest parzysta.
Uzasadnij, że kąt ostry między dwusiecznymi kątów ostrych trójkąta prostokątnego jest równy 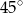 .
.