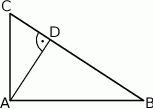
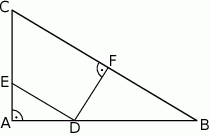
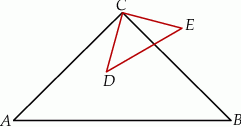
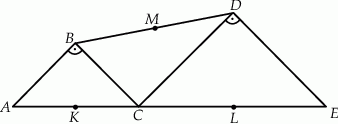
Dany jest trójkąt prostokątny  , w którym
, w którym  oraz
oraz  . Punkty
. Punkty 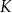 i
i 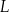 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 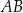 i
i 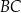 tak, że
tak, że 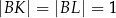 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 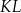 przecina wysokość
przecina wysokość 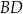 tego trójkąta w punkcie
tego trójkąta w punkcie 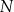 , a ponadto
, a ponadto 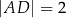 .
.
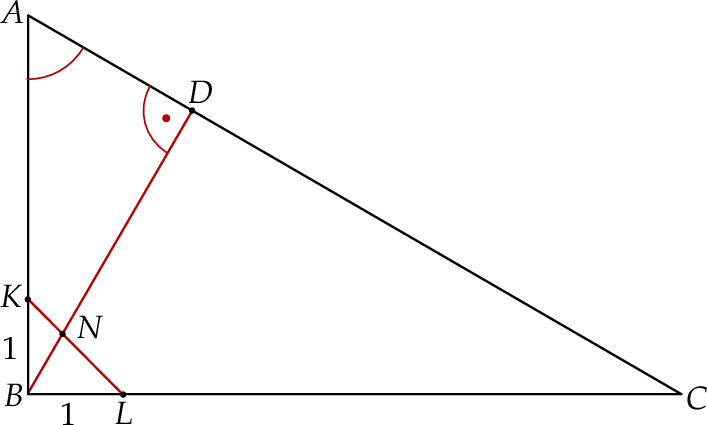
Wykaż, że 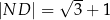 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt prostokątny 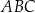 , w którym
, w którym 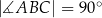 oraz
oraz 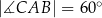 . Punkty
. Punkty 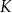 i
i 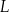 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 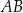 i
i 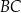 tak, że
tak, że 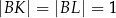 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 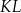 przecina wysokość
przecina wysokość 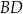 tego trójkąta w punkcie
tego trójkąta w punkcie 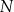 , a ponadto
, a ponadto 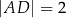 .
.
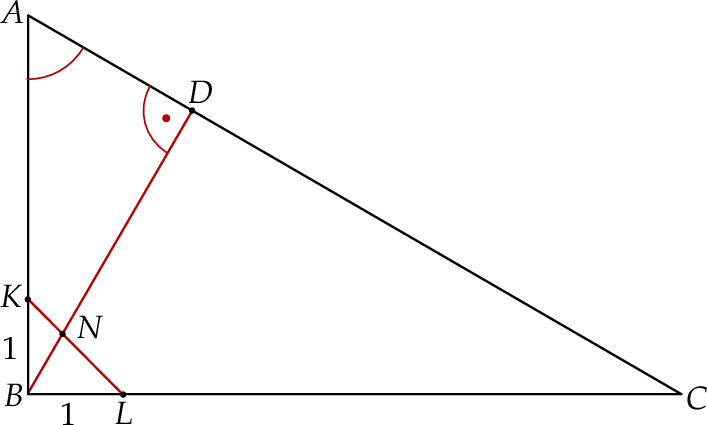
Wykaż, że 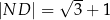 .
.
Wykaż, że wysokość 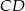 trójkąta prostokątnego
trójkąta prostokątnego 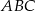 poprowadzona z wierzchołka
poprowadzona z wierzchołka 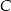 kąta prostego dzieli przeciwprostokątną na odcinki
kąta prostego dzieli przeciwprostokątną na odcinki 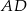 i
i 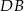 , których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio
, których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio 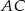 i
i 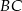 tego trójkąta.
tego trójkąta.
Dany jest trójkąt prostokątny 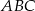 , w którym
, w którym 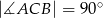 i
i 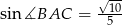 . Niech
. Niech 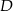 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 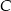 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 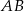 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 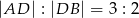 .
.
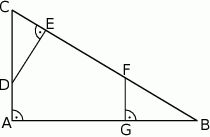
Dany jest trójkąt prostokątny 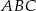 . Na przyprostokątnych
. Na przyprostokątnych 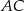 i
i 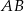 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 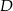 i
i 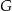 . Na przeciwprostokątnej
. Na przeciwprostokątnej 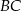 wyznaczono punkty
wyznaczono punkty  i
i  takie, że
takie, że 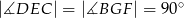 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 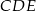 jest podobny do trójkąta
jest podobny do trójkąta 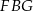 .
.
Dany jest trójkąt prostokątny  . Na przyprostokątnych
. Na przyprostokątnych 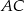 i
i 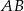 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 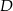 i
i 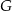 . Na przeciwprostokątnej
. Na przeciwprostokątnej 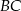 wyznaczono punkty
wyznaczono punkty  i
i  takie, że
takie, że 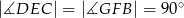 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 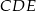 jest podobny do trójkąta
jest podobny do trójkąta 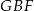 .
.
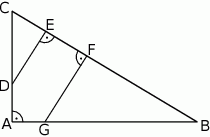
Dany jest trójkąt prostokątny 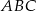 . Na przyprostokątnych
. Na przyprostokątnych 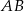 i
i 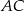 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 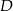 i
i 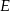 takie, że
takie, że 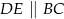 . Na przeciwprostokątnej
. Na przeciwprostokątnej 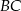 wyznaczono punkt
wyznaczono punkt 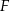 taki, że
taki, że 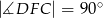 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 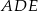 jest podobny do trójkąta
jest podobny do trójkąta 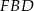 .
.
Na zewnątrz równoramiennego trójkąta prostokątnego o przyprostokątnych równych  zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 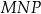 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 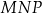 jest równe
jest równe 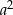 .
.
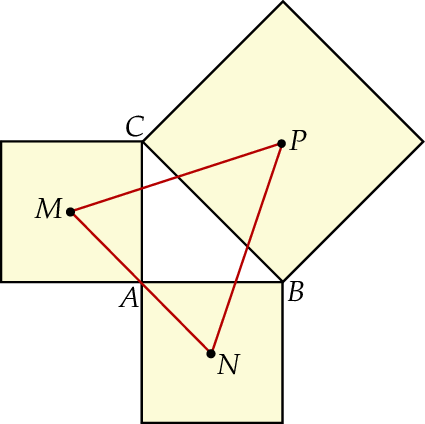
Na zewnątrz równoramiennego trójkąta prostokątnego  zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 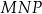 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 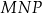 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 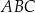 .
.
Uzasadnij, że nie istnieje trójkąt prostokątny, w którym przeciwprostokątna ma długość 24, a kąty ostre  i
i 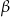 są takie, że
są takie, że 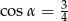 i
i 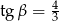 .
.
Wykaż, że jeżeli pole koła opisanego na trójkącie prostokątnym jest 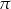 razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
Trójkąty prostokątne równoramienne 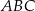 i
i 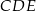 są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 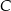 jest prosty). Wykaż, że
jest prosty). Wykaż, że 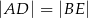 .
.
Trójkąty prostokątne równoramienne  i
i 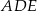 są położone tak, jak na poniższym rysunku.
są położone tak, jak na poniższym rysunku.
Wykaż, że 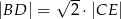 .
.
Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.
Rozważmy trójkąt prostokątny 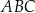 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 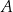 . Niech każdy z boków tego trójkąta:
. Niech każdy z boków tego trójkąta: 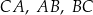 będzie podstawą trójkątów podobnych, odpowiednio:
będzie podstawą trójkątów podobnych, odpowiednio: 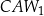 ,
, 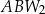 ,
, 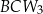 . Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach:
. Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: 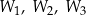 .
.

Pola trójkątów: 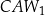 ,
, 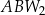 ,
, 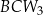 oznaczymy odpowiednio jako
oznaczymy odpowiednio jako 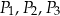 . Udowodnij, że
. Udowodnij, że
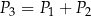
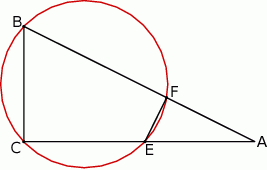
Okrąg przechodzący przez końce przyprostokątnej 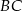 trójkąta prostokątnego
trójkąta prostokątnego 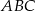 przecina drugą przyprostokątną
przecina drugą przyprostokątną 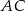 oraz przeciwprostokątną
oraz przeciwprostokątną 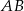 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 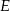 i
i 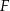 . Wykaż, że promień okręgu opisanego na trójkącie
. Wykaż, że promień okręgu opisanego na trójkącie 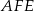 jest równy
jest równy 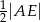 .
.
Punkt  przyprostokątnej
przyprostokątnej 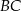 trójkąta prostokątnego
trójkąta prostokątnego 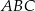 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 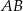 otrzymując punkt
otrzymując punkt 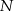 . Wykaż, że
. Wykaż, że 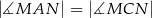 .
.
W trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 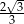 . Wykaż, że iloczyn sinusów tych kątów jest równy
. Wykaż, że iloczyn sinusów tych kątów jest równy 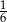 .
.
W trójkącie prostokątnym suma sinusów kątów ostrych jest równa  . Wykaż, że iloczyn cosinusów tych kątów jest równy
. Wykaż, że iloczyn cosinusów tych kątów jest równy  .
.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 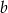 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 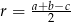 .
.
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy dłuższy od drugiego.
W trójkącie prostokątnym jedna przyprostokątna jest 3 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 9 razy dłuższy od drugiego.
Wykaż, że jeśli 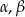 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 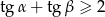 .
.
W trójkącie prostokątnym 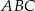 przyprostokątne mają długości
przyprostokątne mają długości 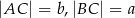 , a wysokość opuszczona z wierzchołka kąta prostego ma długość
, a wysokość opuszczona z wierzchołka kąta prostego ma długość 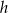 .
.
Wykaż, że jeżeli 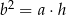 to
to  .
.
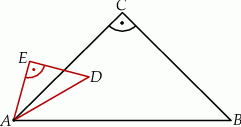
Trójkąty 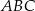 i
i 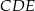 są prostokątne oraz
są prostokątne oraz 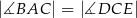 . Punkty
. Punkty 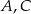 i
i 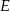 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 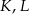 i
i 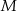 są środkami odcinków
są środkami odcinków 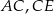 i
i 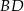 (zobacz rysunek). Wykaż, że kąt
(zobacz rysunek). Wykaż, że kąt 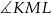 jest prosty.
jest prosty.
Trójkąty 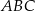 i
i 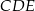 są równoramienne i prostokątne. Punkty
są równoramienne i prostokątne. Punkty 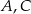 i
i 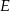 leżą na jednej prostej, a punkty
leżą na jednej prostej, a punkty 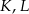 i
i 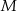 są środkami odcinków
są środkami odcinków 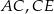 i
i 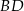 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 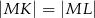 .
.
Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
Na przyprostokątnych  i
i  trójkąta prostokątnego
trójkąta prostokątnego  zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 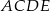 i
i 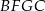 . Odcinek
. Odcinek 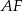 przecina przyprostokątną
przecina przyprostokątną 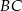 w punkcie
w punkcie 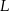 , a odcinek
, a odcinek 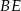 przecina przyprostokątną
przecina przyprostokątną 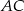 w punkcie
w punkcie 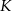 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 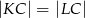 .
.
Trójkąt  jest prostokątny. Punkt
jest prostokątny. Punkt  jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 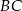 oraz
oraz 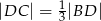 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 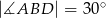 .
.