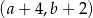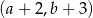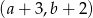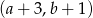Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 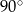 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
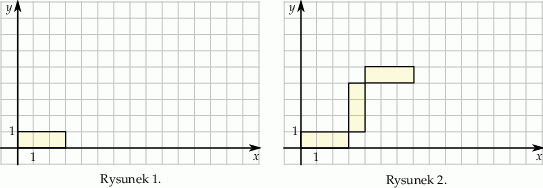
Marcel narysował w ten sposób pięć prostokątów. Współrzędna
 prawego górnego wierzchołka piątego prostokąta jest równa
prawego górnego wierzchołka piątego prostokąta jest równaA) 11 B) 10 C) 9 D) 8

 jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to 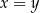
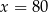
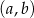 . Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe
. Współrzędne prawego górnego wierzchołka kolejnego prostokąta są równe 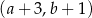
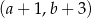
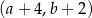
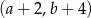
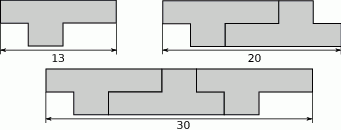

 ma długość
ma długość
 ma długość
ma długość będzie całkowitą szerokością wzoru ułożonego z
będzie całkowitą szerokością wzoru ułożonego z  płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 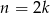 jest liczbą parzystą, to
jest liczbą parzystą, to 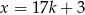 .
. 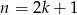 jest liczbą nieparzystą, to
jest liczbą nieparzystą, to 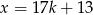
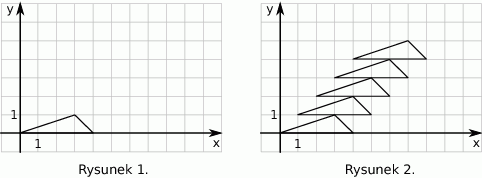
 trójkątów. Współrzędna
trójkątów. Współrzędna  górnego wierzchołka tego trójkąta jest równa
górnego wierzchołka tego trójkąta jest równa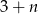
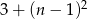
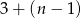

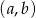 . Współrzędne środka podstawy w następnym trójkącie będą równe
. Współrzędne środka podstawy w następnym trójkącie będą równe 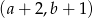
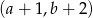
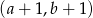
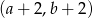
 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 1.
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 1. 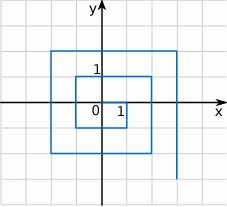
 jest liczbą parzystą, to odcinek o numerze
jest liczbą parzystą, to odcinek o numerze  jest równoległy do osi
jest równoległy do osi 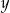 .
.  jest liczbą nieparzystą, to długość odcinka o numerze
jest liczbą nieparzystą, to długość odcinka o numerze  jest równa
jest równa 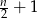 .
.
 i wysokości 11 cegieł potrzeba
i wysokości 11 cegieł potrzeba 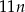 cegieł.
cegieł. 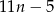 cegieł.
cegieł. 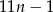 cegieł.
cegieł. 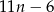 cegieł.
cegieł. 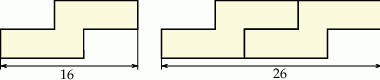

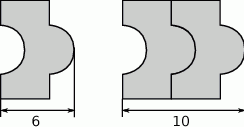
 ma długość
ma długość odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek? 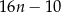
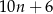
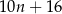
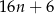
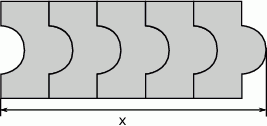
 ma długość
ma długość odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek? 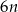
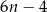
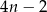
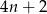
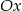 , przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi
, przesunięcia o 3 jednostki w prawo, i odsunięcia o 1 jednostkę od osi 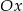 (rysunek 2.).
(rysunek 2.). 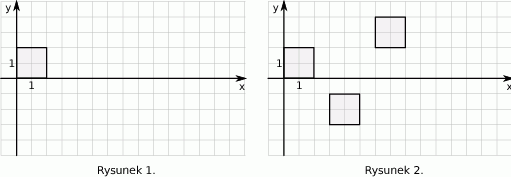
 środka tego kwadratu jest równa
środka tego kwadratu jest równa 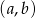 i
i 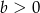 , to współrzędne środka kolejnego kwadratu będą równe
, to współrzędne środka kolejnego kwadratu będą równe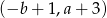
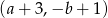
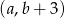
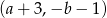
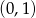 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 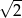 .
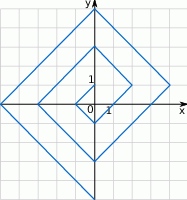
. 
 jest liczbą parzystą, to odcinek o numerze
jest liczbą parzystą, to odcinek o numerze  jest równoległydo odcinka o numerze 3.
jest równoległydo odcinka o numerze 3. jest liczbą nieparzystą, to długość odcinka o numerze
jest liczbą nieparzystą, to długość odcinka o numerze  jest równa
jest równa 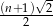 .
. 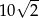 .
.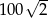 .
.  budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2. 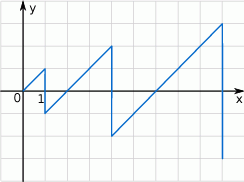
 jest liczbą nieparzystą, to odcinek o numerze
jest liczbą nieparzystą, to odcinek o numerze  jest równoległy doodcinka o numerze 1.
jest równoległy doodcinka o numerze 1. jest liczbą parzystą, to długość odcinka o numerze
jest liczbą parzystą, to długość odcinka o numerze  jest równa
jest równa 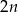 .
. 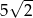 .
.  jest liczbą parzystą, to długość odcinka o numerze
jest liczbą parzystą, to długość odcinka o numerze 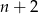 jest o 2 większa od długości odcinka o numerze
jest o 2 większa od długości odcinka o numerze  .
. 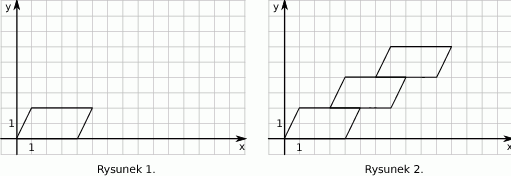
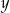 prawego górnego wierzchołka tego równoległoboku jest równa
prawego górnego wierzchołka tego równoległoboku jest równa równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równa
równoległoboków. Współrzędna y prawego górnego wierzchołka ostatniego równoległoboku jest równa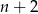
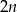
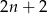
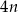
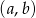 . Współrzędne takiego wierzchołka w następnym równoległoboku będą równe
. Współrzędne takiego wierzchołka w następnym równoległoboku będą równe