Boki 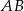 i
i 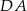 rombu
rombu 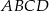 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 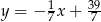 i
i 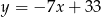 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 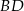 tego rombu, jeżeli jego środek ma współrzędne
tego rombu, jeżeli jego środek ma współrzędne 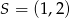 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Romb
Przekątna 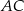 rombu
rombu 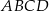 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 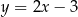 . Wierzchołki
. Wierzchołki 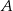 i
i 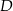 mają współrzędne
mają współrzędne 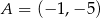 i
i 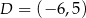 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 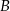 i
i 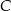 oraz pole rombu
oraz pole rombu 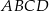 .
.
Punkt 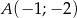 jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej
jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej 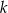 o równaniu
o równaniu 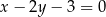 . Środkiem symetrii tego rombu jest punkt
. Środkiem symetrii tego rombu jest punkt 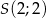 . Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
. Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
Dany jest okrąg 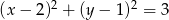 . Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 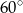 .
.
Dany jest okrąg 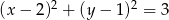 . Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 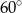 .
.
Przekątne 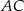 i
i 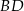 rombu
rombu 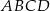 przecinają się w punkcie
przecinają się w punkcie 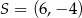 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 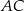 wiedząc, że prosta zawierająca przekątną
wiedząc, że prosta zawierająca przekątną 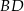 ma równanie
ma równanie 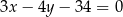 .
.
Przekątne rombu 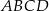 przecinają się w punkcie
przecinają się w punkcie 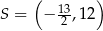 . Punkty
. Punkty 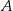 i
i 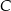 leżą na prostej o równaniu
leżą na prostej o równaniu 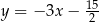 . Wyznacz równanie prostej
. Wyznacz równanie prostej 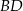 .
.
Przekątne rombu 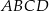 przecinają się w punkcie
przecinają się w punkcie 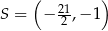 . Punkty
. Punkty 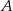 i
i 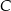 leżą na prostej o równaniu
leżą na prostej o równaniu 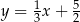 . Wyznacz równanie prostej
. Wyznacz równanie prostej 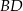 .
.
Punkt 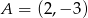 jest wierzchołkiem rombu
jest wierzchołkiem rombu 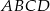 o polu równym 300. Punkt
o polu równym 300. Punkt 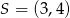 jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Punkty przecięcia paraboli 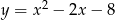 z prostą
z prostą 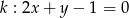 są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
Punkty 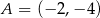 i
i 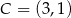 są wierzchołkami rombu
są wierzchołkami rombu 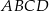 , którego wierzchołek
, którego wierzchołek 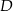 leży na prostej
leży na prostej 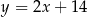 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 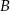 i
i 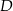 .
.
Dane są punkty 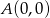 i
i 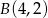 .
.
- Znajdź takie punkty
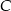 i
i 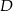 aby trójkąty
aby trójkąty 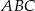 i
i 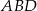 były równoboczne.
były równoboczne. - Znajdź równanie okręgu wpisanego w romb
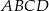 .
. - Oblicz pole figury, którą otrzymamy po usunięciu z rombu
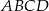 wnętrza wpisanego w niego koła.
wnętrza wpisanego w niego koła.
Punkty 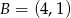 i
i 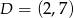 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 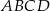 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 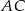 tego rombu.
tego rombu.
Punkty 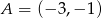 i
i 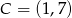 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 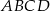 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 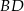 tego rombu.
tego rombu.
Prosta o równaniu 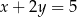 zawiera przekątną
zawiera przekątną 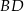 rombu
rombu 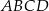 , którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli
, którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli 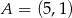 .
.
Punkty 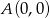 oraz
oraz 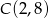 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 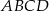 o boku długości
o boku długości 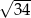 . Wyznacz współrzędne pozostałych wierzchołków tego rombu.
. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Oblicz pole i obwód rombu 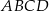 wiedząc, że przekątna
wiedząc, że przekątna 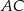 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 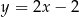 oraz
oraz 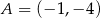 i
i 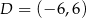 .
.
Punkty 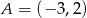 i
i 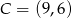 są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
W rombie 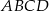 , którego pole jest równe 10 dane są przeciwległe wierzchołki
, którego pole jest równe 10 dane są przeciwległe wierzchołki 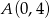 i
i 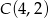 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Punkty 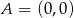 i
i 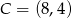 są wierzchołkami rombu
są wierzchołkami rombu 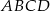 , którego jeden z boków zawiera się w prostej
, którego jeden z boków zawiera się w prostej 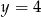 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Na okręgu o równaniu 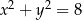 opisano romb o polu
opisano romb o polu 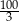 . Dłuższa przekątna rombu zawiera się w prostej o równaniu
. Dłuższa przekątna rombu zawiera się w prostej o równaniu 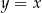 . Oblicz współrzędne wierzchołków tego rombu.
. Oblicz współrzędne wierzchołków tego rombu.
Punkt 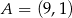 jest wierzchołkiem rombu
jest wierzchołkiem rombu 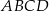 o polu 60. Przekątna
o polu 60. Przekątna 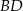 zawiera się w prostej
zawiera się w prostej 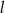 o równaniu
o równaniu 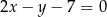 . Wyznacz równanie okręgu wpisanego w ten romb.
. Wyznacz równanie okręgu wpisanego w ten romb.
W rombie 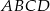 dane są
dane są 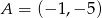 i punkt przecięcia przekątnych
i punkt przecięcia przekątnych 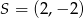 . Wierzchołek
. Wierzchołek 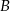 leży na prostej
leży na prostej 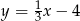 . Oblicz współrzędne pozostałych wierzchołków rombu.
. Oblicz współrzędne pozostałych wierzchołków rombu.
Punkt 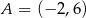 jest wierzchołkiem rombu
jest wierzchołkiem rombu 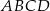 o polu 90. Przekątna
o polu 90. Przekątna 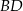 zawiera się w prostej
zawiera się w prostej 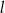 o równaniu
o równaniu 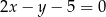 . Wyznacz długość boku tego rombu.
. Wyznacz długość boku tego rombu.
Punkty przecięcia paraboli 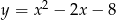 z prostą
z prostą 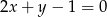 są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.

