Malarz chcąc rozjaśnić 20 litrów granatowej farby postąpił w następujący sposób: odlał jeden litr farby i dolał 1 litr farby białej, a potem całość dokładnie wymieszał. Procedurę tę powtórzył w sumie 8 razy. Ile litrów granatowej farby pozostało w otrzymanej mieszaninie? Wynik podaj z dokładnością do 1 litra.
/Szkoła średnia/Zadania z treścią/Zmiana ilości
W skarbcu królewskim było 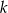 monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę
monet. Pierwszego dnia rano skarbnik dorzucił 25 monet, a każdego następnego ranka dorzucał o 2 monety więcej niż dnia poprzedniego. Jednocześnie ze skarbca król zabierał w południe każdego dnia 50 monet. Oblicz najmniejszą liczbę 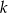 , dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości
, dla której w każdym dniu w skarbcu była co najmniej jedna moneta, a następnie dla tej wartości 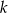 oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
oblicz, w którym dniu w skarbcu była najmniejsza liczba monet.
Parking wyłożono płytami betonowymi w kształcie prostokątów. Gdyby ten sam parking wyłożyć prostokątnymi płytami o powierzchni większej o 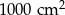 to liczba użytych płyt zmniejszyłaby się o 8. Gdyby natomiast użyć płyt o powierzchni mniejszej o
to liczba użytych płyt zmniejszyłaby się o 8. Gdyby natomiast użyć płyt o powierzchni mniejszej o 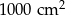 , to liczba użytych płyt zwiększyłaby się o 12. Oblicz pole powierzchni parkingu.
, to liczba użytych płyt zwiększyłaby się o 12. Oblicz pole powierzchni parkingu.
W chwili początkowej 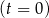 masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej
masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 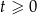 funkcja
funkcja 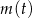 określa masę substancji w gramach po
określa masę substancji w gramach po 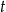 pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji
pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 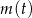 . Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.
. Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.
W chwili początkowej 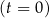 masa substancji jest równa 12 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 21% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej
masa substancji jest równa 12 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 21% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 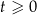 funkcja
funkcja 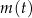 określa masę substancji w gramach po
określa masę substancji w gramach po 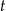 pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji
pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 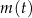 . Oblicz, przez ile pełnych dób masa tej substancji będzie przekraczać 3 gramy.
. Oblicz, przez ile pełnych dób masa tej substancji będzie przekraczać 3 gramy.
W hurtowni owoców zmagazynowano 15 ton jabłek. Codziennie hurtownia sprzedaje 120kg jabłek.
- Napisz wzór wyrażający zależność między ilością jabłek pozostających w hurtowni a liczbą dni sprzedaży.
- Określ dziedzinę otrzymanej funkcji.
- Podaj na ile dni sprzedaży wystarczy zgromadzonych jabłek.
W dwóch sadach rosło razem 8400 drzewek. W ciągu roku zwiększono liczbę drzewek w każdym sadzie. W pierwszym o 20%, a w drugim o 50%. Okazało się wtedy, że liczba drzewek w pierwszym sadzie jest 2 razy większa niż w drugim. Ile drzew było początkowo w każdym sadzie?
W dwóch silosach zbożowych znajdowało się łącznie 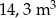 zboża. W ciągu dwóch tygodni zwiększono ilość zboża w pierwszym silosie o 28%, a w drugim o 60%. Po tej zmianie ilość zboża w pierwszym silosie jest dwa razy mniejsza od ilości zboża w drugim silosie. Ile metrów sześciennych zboża znajdowało się początkowo w każdym z silosów?
zboża. W ciągu dwóch tygodni zwiększono ilość zboża w pierwszym silosie o 28%, a w drugim o 60%. Po tej zmianie ilość zboża w pierwszym silosie jest dwa razy mniejsza od ilości zboża w drugim silosie. Ile metrów sześciennych zboża znajdowało się początkowo w każdym z silosów?
Czas 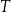 połowicznego rozpadu węgla
połowicznego rozpadu węgla 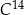 to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla
to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla 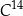 wynosi około
wynosi około 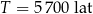 , a pozostała masa tego izotopu wyraża się wzorem
, a pozostała masa tego izotopu wyraża się wzorem
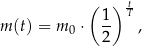
gdzie:
-
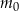 – masa izotopu węgla
– masa izotopu węgla 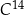 w trakcie życia organizmu
w trakcie życia organizmu -
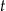 – czas jaki upłynął od czasu śmierci organizmu.
– czas jaki upłynął od czasu śmierci organizmu.
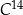 stanowi
stanowi 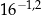 masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne.
masy tego izotopu, jaka utrzymywała się podczas życia tego organizmu. Oblicz, ile lat mają odkryte szczątki organiczne. Czas 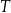 połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder
połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder 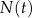 izotopu promieniotwórczego pozostających w próbce po czasie
izotopu promieniotwórczego pozostających w próbce po czasie 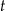 , licząc od chwili
, licząc od chwili 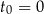 , wyraża się zależnością wykładniczą:
, wyraża się zależnością wykładniczą:
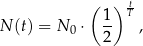
gdzie 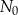 jest liczbą jąder izotopu promieniotwórczego w chwili początkowej
jest liczbą jąder izotopu promieniotwórczego w chwili początkowej 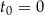 . Czas połowicznego rozpadu węgla
. Czas połowicznego rozpadu węgla 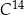 to około 5 700 lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla
to około 5 700 lat. Naukowcy oszacowali za pomocą datowania radiowęglowego, że masa izotopu węgla 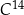 w pewnym organicznym znalezisku archeologicznym stanowi
w pewnym organicznym znalezisku archeologicznym stanowi 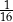 masy tego izotopu, jaka utrzymywała się podczas życia organizmu. Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.
masy tego izotopu, jaka utrzymywała się podczas życia organizmu. Oblicz, ile lat ma opisane znalezisko archeologiczne. Wynik podaj z dokładnością do stu lat.
Szachownica do gry w szachy ma 64 pola. Przypuśćmy, że pierwsze pole ma wartość 1 grosza, drugie 2 groszy, trzecie 4 groszy, czwarte 8 groszy itd. Jaki jest jest najmniejszy numer pola szachownicy, którego wartość przekracza 1 000 000 zł?
Czas 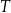 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 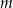 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
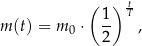
gdzie:
-
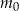 – masa przyjętej dawki leku,
– masa przyjętej dawki leku, -
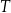 – czas półtrwania leku,
– czas półtrwania leku, -
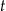 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pacjent otrzymuje co 4 dni o tej samej godzinie dawkę 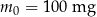 leku L. Czas półtrwania tego leku w organizmie jest równy
leku L. Czas półtrwania tego leku w organizmie jest równy 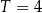 doby.
doby.
Oblicz masę leku L w organizmie tego pacjenta tuż przed przyjęciem jedenastej dawki tego leku. Wynik podaj w zaokrągleniu do 0,1 mg.
Czas 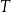 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 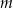 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
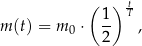
gdzie:
-
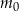 – masa przyjętej dawki leku
– masa przyjętej dawki leku -
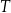 – czas półtrwania leku
– czas półtrwania leku -
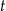 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.
W przypadku przyjęcia kilku(nastu) dawek powyższa zależność pozwala obliczyć, ile leku pozostało w danym momencie w organizmie z każdej poprzednio przyjętej dawki. W ten sposób obliczone masy leku z przyjętych poprzednich dawek sumują się i dają informację o całkowitej aktualnej masie leku w organizmie.
Pan Karol otrzymuje codziennie o godz. 12:00 dawkę 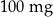 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 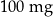 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 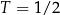 doby.
doby.
Oblicz masę leku L w organizmie pana Tomasza tuż przed przyjęciem szóstej dawki tego leku. Wynik podaj w zaokrągleniu do 0,01 mg.
Liczebność kolonii bakterii pewnego szczepu w zależności od czasu opisuje funkcja 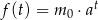 , gdzie
, gdzie 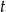 – oznacza czas obserwacji w godzinach,
– oznacza czas obserwacji w godzinach,  – pewną stałą dodatnią, a
– pewną stałą dodatnią, a 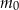 – liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
– liczebność początkowej próby bakterii. Na początku doświadczenia zaobserwowano 300 sztuk bakterii. Po dwóch godzinach liczba bakterii wzrosła do 1200. Po jakim czasie liczba bakterii wzrośnie do 153600?
Pusty zbiornik można zapełnić wodą z dwóch źródeł. Jeżeli będziemy nalewać wodę z pierwszego źródła przez 5 godzin, następnie zamkniemy to źródło i będziemy nalewać z drugiego przez 10 godzin, to zbiornik napełni się w 35%. Jeżeli natomiast będziemy napełniać zbiornik jednocześnie z dwóch źródeł, to zbiornik zostanie całkowicie napełniony w ciągu 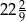 godzin. Ile godzin potrzeba do napełnienia całego zbiornika za pomocą każdego z źródeł osobno?
godzin. Ile godzin potrzeba do napełnienia całego zbiornika za pomocą każdego z źródeł osobno?
Masa 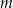 leku
leku 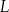 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
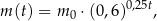
gdzie:
-
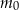 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 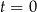 dawki leku,
dawki leku, -
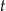 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 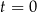 zażycia leku.
zażycia leku.
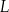 w dawce 200 mg. Oblicz, ile mg leku
w dawce 200 mg. Oblicz, ile mg leku 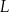 pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 12 godzinach od momentu przyjęcia dawki. Masa 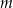 leku
leku 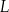 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
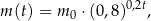
gdzie:
-
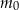 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 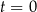 dawki leku,
dawki leku, -
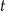 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 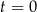 zażycia leku.
zażycia leku.
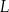 w dawce 300 mg. Oblicz, ile mg leku
w dawce 300 mg. Oblicz, ile mg leku 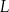 pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki.
pozostanie w organizmie chorego po 15 godzinach od momentu przyjęcia dawki. Masa 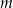 leku
leku 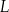 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
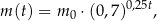
gdzie:
-
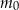 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 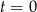 dawki leku,
dawki leku, -
 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu  zażycia leku.
zażycia leku.
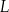 w dawce 80 mg. Oblicz, po ilu godzinach od momentu przyjęcia dawki, w organizmie chorego pozostanie 39,2 mg leku
w dawce 80 mg. Oblicz, po ilu godzinach od momentu przyjęcia dawki, w organizmie chorego pozostanie 39,2 mg leku 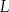 .
. W kartonach rozmieszczono 2800 metalowych puszek w ten sposób, że w każdym kartonie znajduje się ta sama liczba puszek. Gdyby do każdego kartonu włożyć o 15 puszek mniej, to należałoby użyć o 60 kartonów więcej. W ilu kartonach rozmieszczono puszki?
Dwie partie konserw rybnych, liczące po 1440 konserwy każda, zapakowano w kartony. Każdą z partii zapakowano w ten sposób, że w każdym kartonie znalazła się ta sama liczba konserw, przy czym w przypadku drugiej partii liczbę kartonów zmniejszono o 2 i w kartonach umieszczono o 10 konserw więcej, niż w przypadku kartonów pierwszej partii. Do ilu łącznie kartonów zapakowano te dwie partie konserw?
W karczmie jest 30 litrowa beczka wina napełniona do pełna. Winiarz zaczerpnął 1 litr wina i dolał do beczki 1 litr wody. Postąpił tak 10 razy. Ile czystego wina zostało w beczce.
W dwóch naczyniach jest woda. Gdyby z pierwszego naczynia przelano do drugiego 2 litry wody, to w obu naczyniach byłoby jej tyle samo. Gdyby zaś z drugiego do pierwszego przelano 3 litry wody, to w pierwszym naczyniu byłoby jej sześć razy więcej niż w drugim. Ile jest wody w obu naczyniach?
W pierwszym zbiorniku było cztery razy więcej litrów wody niż w drugim. Do każdego zbiornika wlano po 6 litrów wody. Teraz w pierwszym zbiorniku jest dwa razy więcej litrów wody niż w drugim zbiorniku. Oblicz, ile łącznie litrów wody jest w obu zbiornikach.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 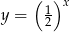 .
.
W przypadku izotopu jodu 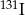 czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g
czas połowicznego rozpadu jest równy 8 dni. Wyznacz najmniejszą liczbę dni, po upływie których pozostanie z 1 g 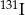 nie więcej niż 0,125 g tego pierwiastka.
nie więcej niż 0,125 g tego pierwiastka.
Czas połowicznego rozpadu pierwiastka to okres, jaki jest potrzebny, by ze 100% pierwiastka pozostało 50% tego pierwiastka. Oznacza to, że ilość pierwiastka pozostała z każdego grama pierwiastka po  okresach rozpadu połowicznego wyraża się wzorem
okresach rozpadu połowicznego wyraża się wzorem 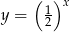 .
.
W przypadku izotopu radu 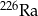 czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g
czas połowicznego rozpadu jest równy 1600 lat. Po ilu latach z 1 g 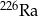 pozostanie nie więcej niż 6,25% masy tego pierwiastka?
pozostanie nie więcej niż 6,25% masy tego pierwiastka?
Masa 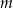 leku
leku 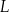 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
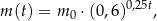
gdzie:
-
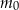 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 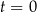 dawki leku,
dawki leku, -
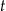 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 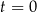 zażycia leku.
zażycia leku.
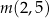 ,
, 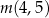 ,
, 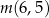 w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu. Masa  leku
leku 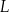 zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
zażytego przez chorego zmienia się w organizmie zgodnie z zależnością wykładniczą
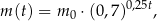
gdzie:
-
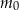 – masa (wyrażona w mg) przyjętej w chwili
– masa (wyrażona w mg) przyjętej w chwili 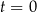 dawki leku,
dawki leku, -
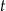 – czas (wyrażony w godzinach) liczony od momentu
– czas (wyrażony w godzinach) liczony od momentu 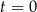 zażycia leku.
zażycia leku.
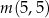 ,
, 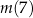 ,
, 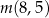 w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu.
w podanej kolejności tworzą ciąg geometryczny. Oblicz iloraz tego ciągu. W chwili początkowej (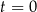 ) zainicjowano pewną reakcję chemiczną, w której brał udział związek
) zainicjowano pewną reakcję chemiczną, w której brał udział związek 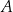 . W wyniku tej reakcji masa
. W wyniku tej reakcji masa 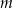 związku
związku 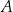 zmieniała się w czasie zgodnie z zależnością
zmieniała się w czasie zgodnie z zależnością
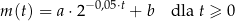
gdzie:
-
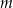 – masa związku
– masa związku 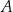 wyrażona w gramach,
wyrażona w gramach, -
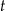 – czas wyrażony w sekundach (liczony od chwili
– czas wyrażony w sekundach (liczony od chwili 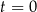 ),
), -
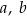 – współczynniki liczbowe.
– współczynniki liczbowe.
Masa początkowa związku 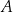 (tj. masa w chwili
(tj. masa w chwili 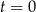 ) była równa
) była równa 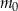 gramów. Po osiągnięciu stanu równowagi (tj. gdy
gramów. Po osiągnięciu stanu równowagi (tj. gdy 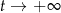 ) masa tego związku była równa
) masa tego związku była równa 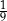 jego masy początkowej (zobacz rysunek).
jego masy początkowej (zobacz rysunek).
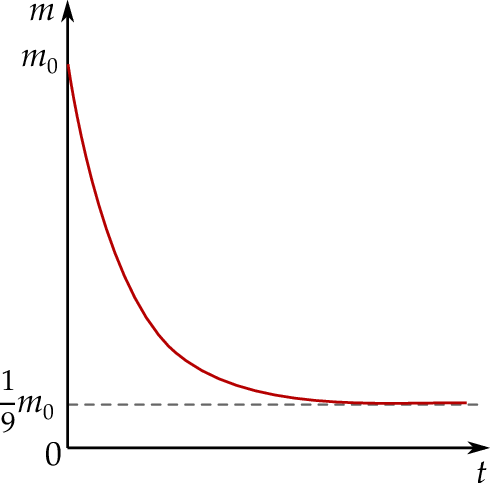
Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało 87,5% masy początkowej tego związku.
Zosia przez 30 dni kwietnia wrzucała do skarbonki pieniądze, przy czym każdego kolejnego dnia wrzucała o 2 zł więcej niż w dniu poprzednim. Wiedząc, że średnio wrzucała 33 zł złotych dziennie, oblicz ile pieniędzy wrzuciła do skarbonki 8 kwietnia.

