Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa 80, pole powierzchni całkowitej jest równe 256 i długości wszystkich krawędzi są nie mniejsze niż 4. Udowodnij, że liczba  może być długością krawędzi takiego prostopadłościanu wtedy i tylko wtedy, gdy
może być długością krawędzi takiego prostopadłościanu wtedy i tylko wtedy, gdy ![[ 28] c ∈ 4, 3](https://img.zadania.info/zad/1810762/HzadT1x.png) .
.
/Szkoła średnia/Geometria/Stereometria/Prostopadłościan
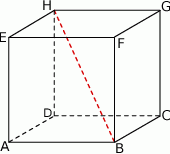
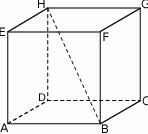
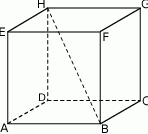
Punkty 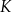 i
i 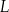 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 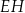 i
i 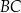 prostopadłościanu
prostopadłościanu 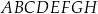 . Przez krawędź
. Przez krawędź 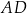 poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem
poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy po kątem 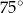 i płaszczyzna ta przecięła odcinek
i płaszczyzna ta przecięła odcinek 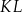 w punkcie
w punkcie 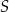 (zobacz rysunek).
(zobacz rysunek).
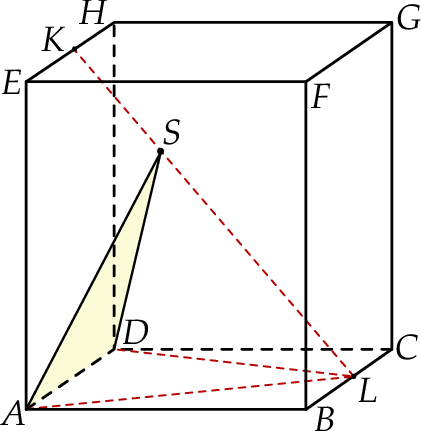
Oblicz pole trójkąta  jeżeli
jeżeli 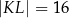 ,
, 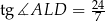 i
i 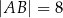 .
.
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są kolejnymi liczbami parzystymi. Pole powierzchni całkowitej prostopadłościanu wynosi 208. Oblicz objętość tego prostopadłościanu.
Długości trzech krawędzi wychodzących z jednego wierzchołka prostopadłościanu są kolejnymi liczbami nieparzystymi. Pole powierzchni całkowitej prostopadłościanu wynosi 142. Oblicz objętość tego prostopadłościanu.
Objętość prostopadłościanu jest równa 405. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 3 : 5. Oblicz pole powierzchni całkowitej prostopadłościanu.
Przekątna prostopadłościanu o długości 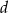 tworzy z odpowiednimi ścianami bocznymi kąty o miarach
tworzy z odpowiednimi ścianami bocznymi kąty o miarach  i
i 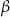 . Wyznacz objętość tego prostopadłościanu.
. Wyznacz objętość tego prostopadłościanu.
W prostopadłościanie 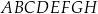 przekątna ściany
przekątna ściany 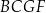 jest o 2 dłuższa od krawędzi
jest o 2 dłuższa od krawędzi 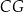 i o 4 dłuższa od krawędzi
i o 4 dłuższa od krawędzi 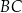 . Przekątna ściany
. Przekątna ściany 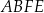 jest nachylona do płaszczyzny
jest nachylona do płaszczyzny  pod kątem
pod kątem  . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Wysokość prostopadłościanu 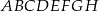 jest równa 1, a długość przekątnej
jest równa 1, a długość przekątnej 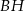 jest równa sumie długości krawędzi
jest równa sumie długości krawędzi 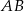 i
i 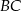 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach 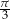 i
i  . Cosinus kąta między tymi przekątnymi jest równy
. Cosinus kąta między tymi przekątnymi jest równy 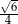 . Wyznacz miarę kąta
. Wyznacz miarę kąta  .
.
Przekątne sąsiednich ścian bocznych prostopadłościanu wychodzące z jednego wierzchołka tworzą z jego podstawą kąty o miarach 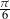 i
i  . Cosinus kąta między tymi przekątnymi jest równy
. Cosinus kąta między tymi przekątnymi jest równy 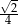 . Wyznacz miarę kąta
. Wyznacz miarę kąta  .
.
Objętość prostopadłościanu jest równa 2400, a mniejsza z jego ścian bocznych ma pole powierzchni 120. Gdyby krótszą z jego krawędzi podstawy wydłużyć o 2, a dłuższą wydłużyć o 5 to objętość prostopadłościanu wzrosłaby o 1100. Oblicz wymiary prostopadłościanu.
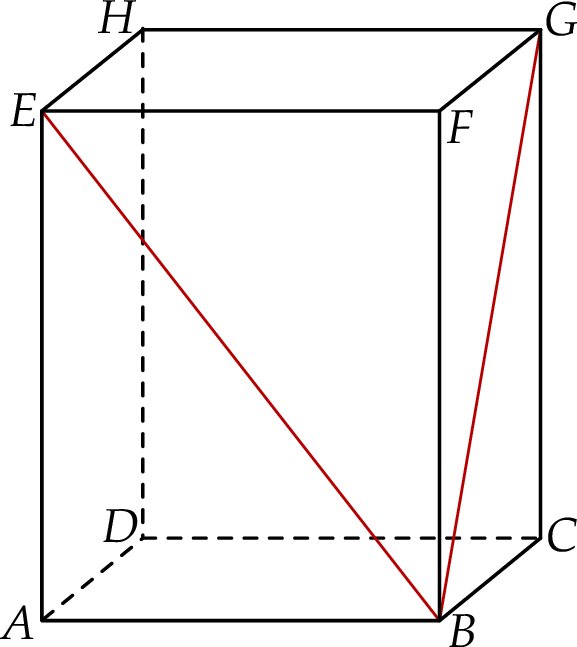
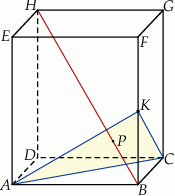
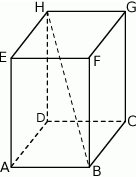
Dany jest prostopadłościan  . Przez wierzchołki
. Przez wierzchołki  i
i  oraz środek
oraz środek 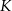 krawędzi
krawędzi 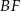 poprowadzono płaszczyznę, która przecina przekątną
poprowadzono płaszczyznę, która przecina przekątną 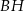 w punkcie
w punkcie 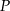 (zobacz rysunek).
(zobacz rysunek).
Oblicz 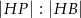 .
.
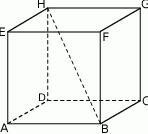
Podstawą graniastosłupa  o objętości 162 jest prostokąt
o objętości 162 jest prostokąt  (zobacz rysunek), którego przekątna tworzy z jego bokiem kąt
(zobacz rysunek), którego przekątna tworzy z jego bokiem kąt 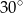 . Przekątna
. Przekątna 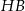 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 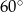 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Podstawą graniastosłupa 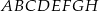 o objętości 162 jest prostokąt
o objętości 162 jest prostokąt 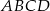 (zobacz rysunek), którego przekątna tworzy z jego bokiem kąt
(zobacz rysunek), którego przekątna tworzy z jego bokiem kąt 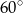 . Przekątna
. Przekątna 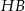 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 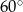 stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
stopni. Oblicz pole powierzchni całkowitej tego graniastosłupa.
Podstawą prostopadłościanu  o wysokości 4 jest kwadrat
o wysokości 4 jest kwadrat  o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne
o boku 3. Oblicz sinus kąta, pod którym przecinają się przekątne 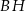 i
i 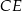 tego prostopadłościanu.
tego prostopadłościanu.
Długości krawędzi podstawy prostopadłościanu są równe 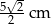 , a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem
, a krawędź boczna ma długość 2 cm. Oblicz pole przekroju tego graniastosłupa płaszczyzną zawierającą przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 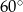 . Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
. Sporządź rysunek i zaznacz na nim przekrój oraz kąt jego nachylenia do płaszczyzny podstawy.
Dany jest graniastosłup prosty 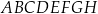 o podstawie prostokątnej
o podstawie prostokątnej 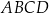 . Przekątne
. Przekątne 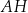 ,
, 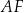 i
i 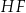 ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka
ścian bocznych tworzą trójkąt ostrokątny o polu 11,25 (zobacz rysunek). Stosunek długości odcinka 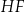 do promienia okręgu opisanego na trójkącie
do promienia okręgu opisanego na trójkącie 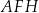 jest równy 30 : 17. Oblicz wysokość
jest równy 30 : 17. Oblicz wysokość 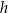 tego graniastosłupa.
tego graniastosłupa.
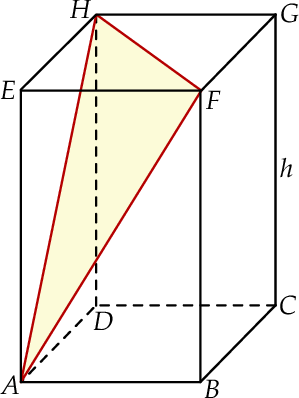
W prostopadłościanie  dane są:
dane są:
gdzie odcinek 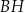 jest przekątną prostopadłościanu, odcinek
jest przekątną prostopadłościanu, odcinek 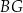 jest przekątną ściany bocznej
jest przekątną ściany bocznej 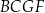 ,
, 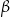 jest miarą kąta
jest miarą kąta 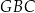 .
.
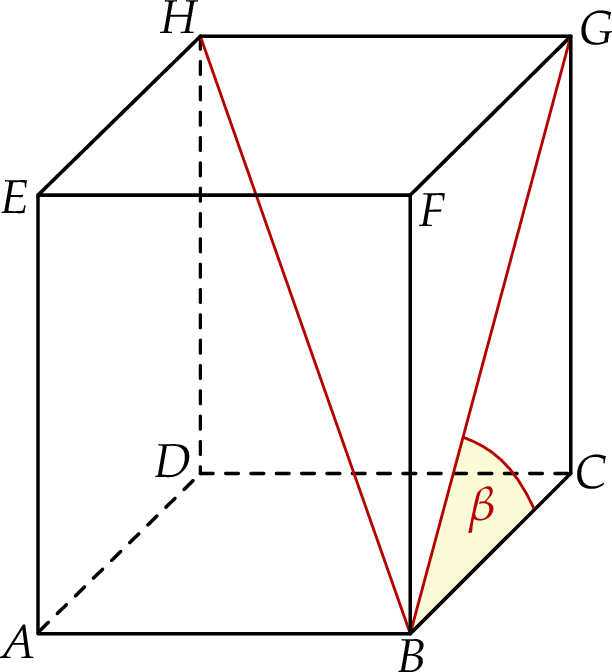
Oblicz pole powierzchni całkowitej prostopadłościanu 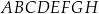 .
.
Dany jest graniastosłup prosty 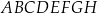 o podstawie prostokątnej
o podstawie prostokątnej 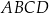 . Przekątne
. Przekątne 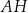 i
i 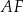 ścian bocznych tworzą kąt ostry o mierze
ścian bocznych tworzą kąt ostry o mierze  takiej, że
takiej, że 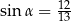 (zobacz rysunek). Pole trójkąta
(zobacz rysunek). Pole trójkąta 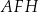 jest równe 26,4. Oblicz wysokość
jest równe 26,4. Oblicz wysokość 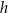 tego graniastosłupa.
tego graniastosłupa.
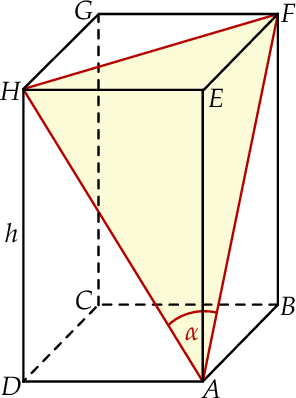
Przekątna prostopadłościanu ma długość 8 cm, a miara kąta, jaki tworzy ona ze ścianą boczną wynosi 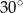 . Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi
. Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi 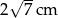 .
.
Przekątna prostopadłościanu ma długość 12 cm, a miara kąta, jaki tworzy ona ze ścianą boczną wynosi 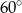 . Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi
. Oblicz objętość prostopadłościanu, jeśli jego wysokość wynosi 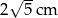 .
.
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 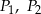 i
i 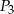 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Podstawą graniastosłupa 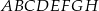 jest prostokąt
jest prostokąt 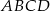 (zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta
(zobacz rysunek), którego krótszy bok ma długość 3. Przekątna prostokąta 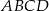 tworzy z jego dłuższym bokiem kąt
tworzy z jego dłuższym bokiem kąt 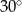 . Przekątna
. Przekątna 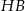 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 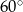 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Podstawą graniastosłupa  jest prostokąt
jest prostokąt 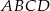 (zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta
(zobacz rysunek), którego dłuższy bok ma długość 6. Przekątna prostokąta 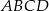 tworzy z jego krótszym bokiem kąt
tworzy z jego krótszym bokiem kąt 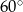 . Przekątna
. Przekątna 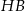 graniastosłupa tworzy z płaszczyzną jego podstawy kąt
graniastosłupa tworzy z płaszczyzną jego podstawy kąt 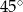 stopni. Oblicz objętość tego graniastosłupa.
stopni. Oblicz objętość tego graniastosłupa.
Przekątna prostopadłościanu ma długość 5 i tworzy z dwoma ścianami prostopadłościanu kąty  i
i 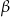 takie, że
takie, że 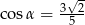 i
i 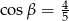 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.

