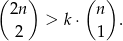Ze zbioru liczb 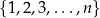 , dla
, dla 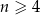 losujemy bez zwracania dwie liczby
losujemy bez zwracania dwie liczby  i
i 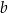 . Oblicz
. Oblicz  jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby
jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby  i
i 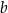 spełniają nierówność
spełniają nierówność
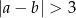
jest równe 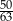 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ze zbioru liczb 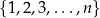 , dla
, dla 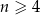 losujemy bez zwracania dwie liczby
losujemy bez zwracania dwie liczby  i
i 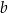 . Oblicz
. Oblicz  jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby
jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby  i
i 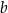 spełniają nierówność
spełniają nierówność
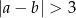
jest równe 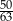 .
.
Niech  będzie liczbą naturalną. Ze zbioru liczb
będzie liczbą naturalną. Ze zbioru liczb 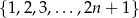 losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od
losujemy dwie liczby (mogą być równe). Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie większa od 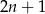 .
.
Dane są dwa podzbiory zbioru liczb całkowitych:
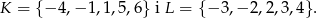
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Ze zbioru pięciu liczb 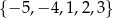 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 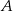 polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia
polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 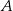 .
.
Dane są dwa podzbiory zbioru liczb całkowitych:
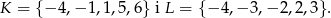
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni.
Dane są dwa podzbiory zbioru liczb całkowitych:
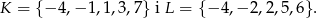
Z każdego z nich losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny.
Ze zbioru 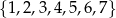 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 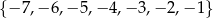 liczbę
liczbę 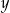 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 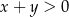 .
.
Ze zbioru 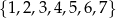 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 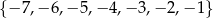 liczbę
liczbę 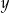 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 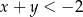 .
.
Ze zbioru 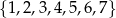 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 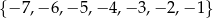 liczbę
liczbę 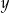 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 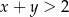 .
.
Ze zbioru liczb 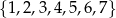 losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 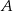 polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
polegającego na tym, że pierwsza z wylosowanych liczb jest nieparzysta, a ich iloczyn jest większy od 10.
Losujemy jedną liczbę całkowitą z przedziału 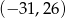 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 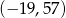 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
Losujemy jedną liczbę całkowitą z przedziału 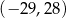 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 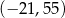 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest ujemny. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru liczb 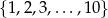 losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
Spośród liczb: -9, -7, -5, -3, -1, 0, 2, 4, 6, 8 losujemy dwie różne liczby  i
i 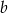 , a następnie zapisujemy ich iloczyn
, a następnie zapisujemy ich iloczyn 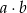 . Oblicz i porównaj prawdopodobieństwa zdarzeń
. Oblicz i porównaj prawdopodobieństwa zdarzeń 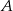 i
i 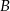 , jeśli:
, jeśli: 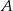 oznacza zdarzenie, że iloczyn
oznacza zdarzenie, że iloczyn 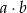 jest liczbą nieujemną;
jest liczbą nieujemną; 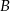 – zdarzenie, że iloczyn
– zdarzenie, że iloczyn 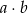 jest liczbą niedodatnią.
jest liczbą niedodatnią.
Ze zbioru 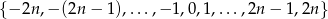 losujemy ze zwracaniem dwie liczby:
losujemy ze zwracaniem dwie liczby:  i
i 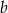 . Rozważmy zdarzenia
. Rozważmy zdarzenia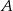 :
: 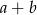 jest liczbą parzystą;
jest liczbą parzystą;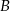 :
: 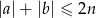 .
.
Oblicz prawdopodobieństwo zdarzenia 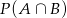 .
.
Dany jest zbiór 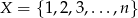 ,
, 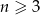 ,
, 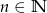 . Ze zbioru
. Ze zbioru 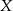 losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
Ze zbioru 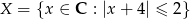 losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez
losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez  oraz
oraz 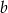 . Oblicz prawdopodobieństwo tego, że wylosowana para liczb
. Oblicz prawdopodobieństwo tego, że wylosowana para liczb 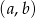 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności 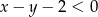 .
.
Ze zbioru 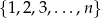 losujemy bez zwracania parę liczb
losujemy bez zwracania parę liczb 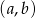 . Dla jakich
. Dla jakich  prawdopodobieństwo wylosowania pary spełniającej warunek
prawdopodobieństwo wylosowania pary spełniającej warunek 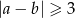 jest większe od
jest większe od 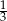 ?
?
Dane są dwa pudełka: czerwone i niebieskie. W każdym z tych pudełek znajduje się 10 kul ponumerowanych liczbami od 1 do 10. Z każdego pudełka losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że numer kuli wylosowanej z czerwonego pudełka jest mniejszy od numeru kuli wylosowanej z niebieskiego pudełka.
Ze zbioru liczb 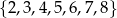 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 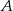 polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
Ze zbioru sześciu liczb 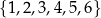 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 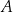 polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
Ze zbioru liczb 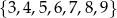 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 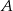 polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
Ze zbioru 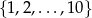 losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki
losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki 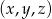 liczb, dla której
liczb, dla której 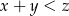 .
.
Z ustalonego zbioru  liczb rzeczywistych losujemy kolejno
liczb rzeczywistych losujemy kolejno 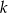 liczb, otrzymując ciąg różnowartościowy
liczb, otrzymując ciąg różnowartościowy 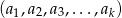 . Zakładając, że
. Zakładając, że 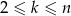 , oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
, oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
Ze zbioru 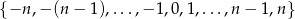 , gdzie
, gdzie 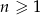 losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż
losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż  .
.
Dany jest ciąg 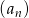 o wyrazie ogólnym
o wyrazie ogólnym 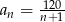 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 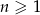 . Ze zbioru liczb
. Ze zbioru liczb 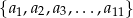 losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno, trzy razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 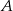 – wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
– wylosujemy trzy liczby całkowite, które będą kolejnymi wyrazami ciągu malejącego.
Ze zbioru liczb naturalnych spełniających nierówność 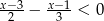 losujemy dwie różne liczby
losujemy dwie różne liczby 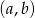 . Oblicz prawdopodobieństwo zdarzenia: punkt o współrzędnych
. Oblicz prawdopodobieństwo zdarzenia: punkt o współrzędnych 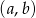 należy do wykresu funkcji
należy do wykresu funkcji 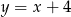 .
.
Dane są dwa zbiory: 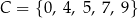 oraz
oraz 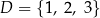 . Losujemy jedną liczbę ze zbioru
. Losujemy jedną liczbę ze zbioru 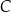 , a następnie losujemy jedną liczbę ze zbioru
, a następnie losujemy jedną liczbę ze zbioru 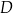 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 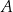 polegającego na tym, że suma wylosowanych liczb będzie większa od 9.
polegającego na tym, że suma wylosowanych liczb będzie większa od 9.
Ze zbioru 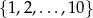 losujemy dwie różne liczby
losujemy dwie różne liczby  i
i 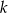 . Oblicz prawdopodobieństwo, że
. Oblicz prawdopodobieństwo, że