Miejscami zerowymi trójmianu 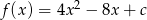 , są liczby całkowite dodatnie. Oblicz
, są liczby całkowite dodatnie. Oblicz  .
.
/Szkoła średnia/Równania/Kwadratowe/Z parametrem/Różne
Różnymi pierwiastkami równania kwadratowego 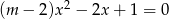 są liczby
są liczby 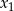 oraz
oraz 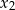 . Narysuj wykres funkcji
. Narysuj wykres funkcji 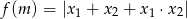 .
.
Wyznacz wszystkie liczby całkowite 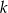 , dla których iloczyn dwóch różnych miejsc zerowych funkcji
, dla których iloczyn dwóch różnych miejsc zerowych funkcji 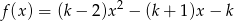 jest liczbą całkowitą.
jest liczbą całkowitą.
Wyznacz dziedzinę i naszkicuj wykres funkcji 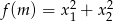 , gdzie
, gdzie 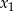 i
i 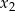 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 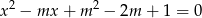 .
.
Wyznacz tę wartość parametru 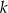 , dla której suma kwadratów dwóch różnych pierwiastków równania
, dla której suma kwadratów dwóch różnych pierwiastków równania 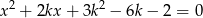 jest największa z możliwych.
jest największa z możliwych.
Dla jakich wartości parametru 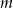 suma kwadratów dwóch różnych pierwiastków równania
suma kwadratów dwóch różnych pierwiastków równania 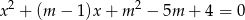 przyjmuje wartość największą. Wyznacz tę wartość.
przyjmuje wartość największą. Wyznacz tę wartość.
Dla jakich wartości parametru 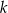 suma kwadratów pierwiastków równania
suma kwadratów pierwiastków równania 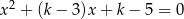 jest najmniejsza?
jest najmniejsza?
Wyznacz wszystkie liczby naturalne dodatnie 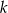 , dla których równanie
, dla których równanie 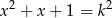 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi.
Dla jakich całkowitych wartości parametru 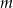 pierwiastkami równania
pierwiastkami równania 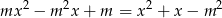 są liczby całkowite?
są liczby całkowite?
Liczby 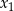 i
i 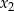 są wszystkimi pierwiastkami rzeczywistymi równania
są wszystkimi pierwiastkami rzeczywistymi równania 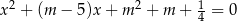 , przy czym zakładamy, że
, przy czym zakładamy, że 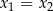 w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru
w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru 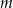 , wyrażenie
, wyrażenie 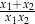 przyjmuje wartość najmniejszą. Oblicz tę wartość.
przyjmuje wartość najmniejszą. Oblicz tę wartość.
Miejscami zerowymi trójmianu kwadratowego 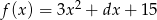 są liczby całkowite. Oblicz
są liczby całkowite. Oblicz 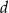 .
.
Rozwiązaniami równania 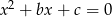 są liczby 8 i -3. Wyznacz parametry
są liczby 8 i -3. Wyznacz parametry 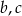 .
.
Funkcja kwadratowa o wzorze 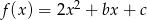 ma dwa miejsca zerowe
ma dwa miejsca zerowe 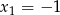 i
i 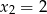 . Wyznacz wartość liczbową współczynników
. Wyznacz wartość liczbową współczynników 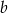 i
i  .
.
Funkcja kwadratowa o wzorze 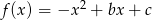 ma dwa miejsca zerowe
ma dwa miejsca zerowe 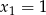 i
i 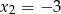 . Wyznacz wartość liczbową współczynników
. Wyznacz wartość liczbową współczynników 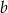 i
i  .
.
Dla jakich wartości parametru 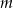 jeden pierwiastek równania
jeden pierwiastek równania 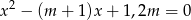 jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?
jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?
Suma współczynników 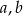 i
i  równania
równania 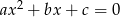 wynosi 24. Różnice
wynosi 24. Różnice 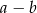 i
i 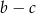 są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
Dla jakich wartości parametru 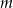 równanie
równanie 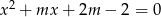 ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta?
ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta?
Wyznacz wszystkie wartości parametru 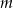 , dla których jedno rozwiązanie równania
, dla których jedno rozwiązanie równania
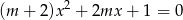
jest sinusem, a drugie cosinusem tego samego kąta?
Podaj wzór i naszkicuj wykres funkcji przyporządkowującej każdej wartości parametru 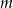 , dla której istnieją dwa różne pierwiastki równania
, dla której istnieją dwa różne pierwiastki równania 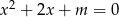 , iloczyn pierwiastków tego równania.
, iloczyn pierwiastków tego równania.
Znajdź tę wartość parametru 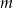 , dla której iloczyn pierwiastków równania
, dla której iloczyn pierwiastków równania 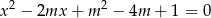 jest najmniejszy.
jest najmniejszy.
Liczba 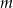 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
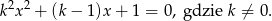
Wyznacz zbiór wartości funkcji określonej wzorem 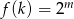 .
.
Liczba 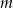 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
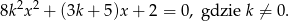
Wyznacz zbiór wartości funkcji określonej wzorem 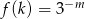 .
.
Jedno z miejsc zerowych trójmianu 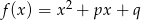 jest równe -1. Znajdź związek między
jest równe -1. Znajdź związek między 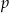 i
i 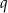 .
.
Funkcja kwadratowa postaci 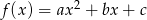 , posiada miejsca zerowe równe -3 i 2, a jej współczynnik
, posiada miejsca zerowe równe -3 i 2, a jej współczynnik 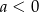 . Oblicz wartości współczynników
. Oblicz wartości współczynników 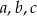 wiedząc, ze największa wartość funkcji wynosi
wiedząc, ze największa wartość funkcji wynosi 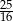 .
.
Dane jest równanie kwadratowe 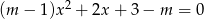 z niewiadomą
z niewiadomą  i parametrem
i parametrem 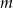 .
.
- Znajdź wzór i dziedzinę funkcji
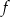 , która zmiennej rzeczywistej
, która zmiennej rzeczywistej 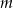 przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji
przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji 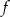 w prostokątnym układzie współrzędnych.
w prostokątnym układzie współrzędnych. - Wykaż, że do wykresu funkcji
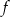 należą tylko trzy punkty o obu współrzędnych całkowitych.
należą tylko trzy punkty o obu współrzędnych całkowitych.
Dla jakich wartości parametru 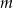 pierwiastkami równania
pierwiastkami równania 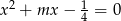 są liczby liczby
są liczby liczby 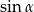 i
i 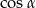 dla pewnego
dla pewnego 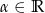 ?
?

