Bok 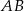 czworokąta
czworokąta 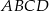 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 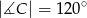 .
.
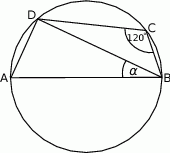
Zatem kąt  ma miarę
ma miarę
A) 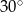 B)
B) 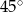 C)
C) 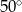 D)
D) 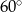
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Bok 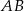 czworokąta
czworokąta 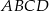 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 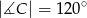 .
.

Zatem kąt  ma miarę
ma miarę
A) 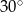 B)
B) 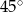 C)
C) 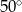 D)
D) 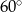
Bok 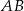 czworokąta
czworokąta 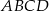 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 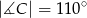 .
.
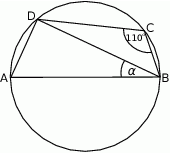
Zatem kąt  ma miarę
ma miarę
A) 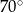 B)
B) 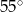 C)
C) 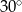 D)
D) 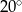
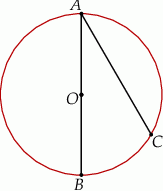
Punkt 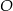 jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy 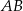 (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
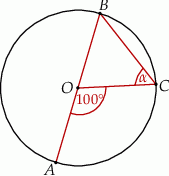
A) 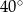 B)
B) 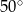 C)
C) 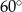 D)
D) 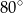
Na okręgu o środku w punkcie 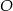 leżą punkty
leżą punkty 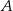 ,
, 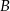 oraz
oraz 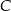 . Odcinek
. Odcinek 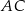 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 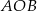 ma miarę
ma miarę 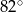 (zobacz rysunek).
(zobacz rysunek).
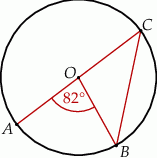
Miara kąta 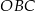 jest równa
jest równa
A) 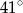 B)
B) 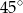 C)
C) 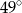 D)
D) 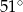
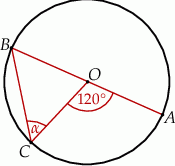
Punkt 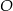 jest środkiem okręgu o średnicy
jest środkiem okręgu o średnicy  (tak jak na rysunku). Kąt
(tak jak na rysunku). Kąt  ma miarę
ma miarę
A) 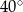 B)
B) 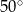 C)
C) 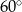 D)
D) 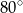
W okręgu o środku 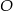 dany jest kąt wpisany
dany jest kąt wpisany 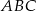 o mierze
o mierze 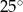 (patrz rysunek).
(patrz rysunek).
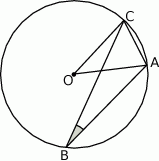
Miara kąta 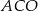 jest równa
jest równa
A) 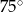 B)
B) 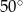 C)
C) 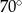 D)
D) 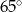
Na okręgu o środku w punkcie 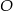 leży punkt
leży punkt 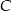 (zobacz rysunek). Odcinek
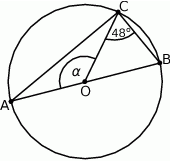
(zobacz rysunek). Odcinek 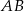 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 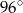 B)
B) 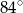 C)
C) 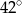 D)
D) 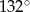
Na okręgu o środku w punkcie 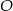 leży punkt
leży punkt 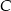 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 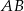 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 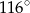 B)
B) 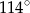 C)
C) 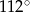 D)
D) 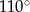
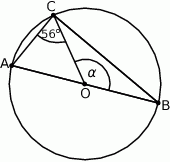
W okręgu o środku 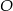 dany jest kąt wpisany
dany jest kąt wpisany 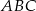 o mierze
o mierze 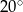 (patrz rysunek).
(patrz rysunek).
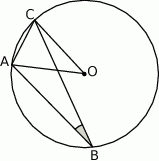
Miara kąta 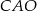 jest równa
jest równa
A) 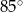 B)
B) 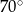 C)
C) 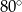 D)
D) 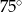
Na okręgu o środku w punkcie 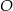 wybrano trzy punkty
wybrano trzy punkty 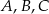 tak, że
tak, że 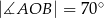 ,
, 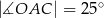 . Cięciwa
. Cięciwa 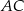 przecina promień
przecina promień 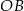 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 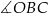 jest równa
jest równa
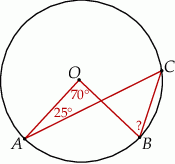
A) 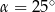 B)
B) 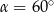 C)
C) 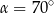 D)
D) 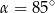
Odcinek 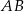 jest średnicą okręgu o środku
jest średnicą okręgu o środku 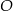 (rysunek).
(rysunek).
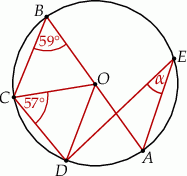
Miara kąta  jest równa
jest równa
A) 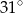 B)
B) 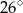 C)
C) 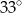 D)
D) 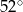
Na okręgu o środku w punkcie 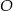 leżą punkty
leżą punkty 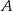 ,
, 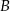 oraz
oraz 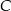 . Odcinek
. Odcinek 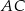 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 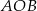 ma miarę
ma miarę 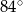 (zobacz rysunek).
(zobacz rysunek).
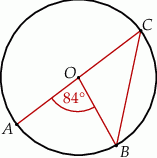
Miara kąta 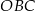 jest równa
jest równa
A) 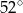 B)
B) 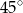 C)
C) 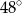 D)
D) 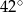
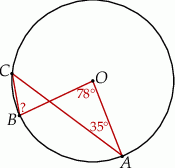
Na okręgu o środku w punkcie 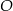 wybrano trzy punkty
wybrano trzy punkty 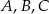 tak, że
tak, że 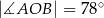 ,
, 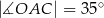 . Cięciwa
. Cięciwa 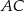 przecina promień
przecina promień 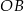 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 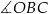 jest równa
jest równa
A) 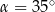 B)
B) 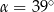 C)
C) 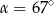 D)
D) 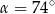
Na okręgu o środku w punkcie 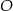 leżą punkty
leżą punkty 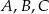 (zobacz rysunek).
(zobacz rysunek).
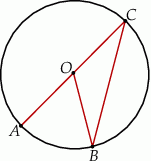
Odcinek 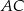 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 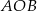 ma miarę
ma miarę 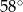 . Kąt
. Kąt 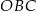 ma miarę równą
ma miarę równą
A) 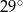 B)
B) 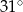 C)
C) 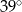 D)
D) 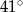
Na okręgu o środku w punkcie 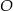 leżą punkty
leżą punkty 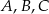 (zobacz rysunek).
(zobacz rysunek).
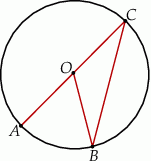
Odcinek 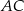 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 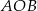 ma miarę
ma miarę 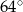 . Kąt
. Kąt 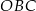 ma miarę równą
ma miarę równą
A) 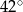 B)
B) 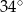 C)
C) 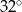 D)
D) 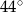
Zaznaczony na rysunku kąt  jest równy
jest równy
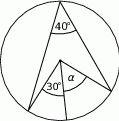
A) 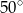 B)
B) 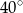 C)
C) 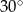 D)
D) 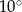
Zaznaczony na rysunku kąt  jest równy
jest równy
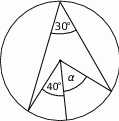
A) 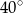 B)
B) 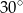 C)
C) 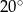 D)
D) 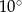
Punkty 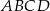 leżą na okręgu o środku
leżą na okręgu o środku 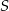 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 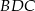 jest równa
jest równa
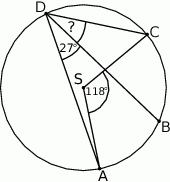
A) 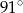 B)
B) 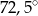 C)
C) 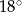 D)
D) 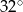
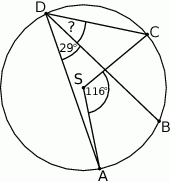
Punkty 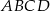 leżą na okręgu o środku
leżą na okręgu o środku 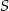 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 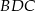 jest równa
jest równa
A) 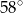 B)
B) 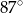 C)
C) 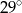 D)
D) 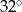
Jaką miarę ma kąt  ?
?
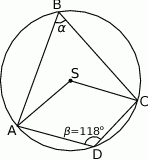
A) 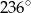 B)
B) 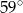 C)
C) 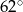 D)
D) 
Jaką miarę ma kąt  ?
?
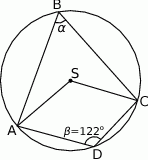
A)  B)
B)  C)
C) 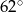 D)
D) 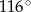
Punkty 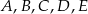 leżą na okręgu o środku
leżą na okręgu o środku 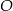 , przy czym
, przy czym 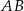 jest średnicą tego okręgu,
jest średnicą tego okręgu, 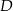 jest środkiem łuku
jest środkiem łuku 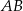 oraz
oraz 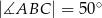 .
.
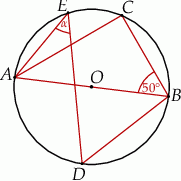
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 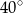 B)
B) 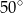 C)
C) 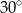 D)
D) 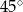
Punkty 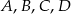 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 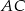 i
i 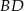 przecinają się w punkcie
przecinają się w punkcie 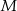 . Zatem
. Zatem
A) 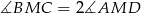 B)
B) 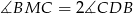 C)
C) 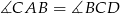 D)
D) 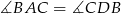
Punkty 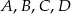 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 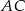 i
i 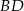 przecinają się w punkcie
przecinają się w punkcie 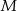 . Zatem
. Zatem
A) 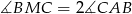 B)
B) 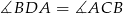 C)
C) 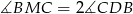 D)
D) 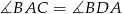
Punkty 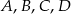 leżą na okręgu w podanej kolejności. Cięciwy
leżą na okręgu w podanej kolejności. Cięciwy 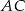 i
i 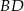 przecinają się w punkcie
przecinają się w punkcie 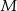 . Zatem
. Zatem
A) 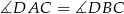 B)
B) 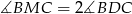 C)
C) 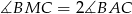 D)
D) 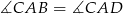
Na rysunku przedstawiono okrąg o środku 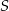 i kąt wpisany o mierze
i kąt wpisany o mierze 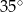 .
.
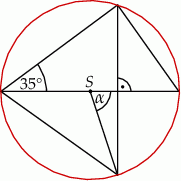
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 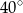 B)
B) 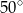 C)
C) 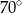 D)
D) 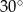
Punkty 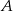 i
i 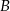 dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o
dzielą okrąg na dwa łuki, przy czym miary kątów wpisanych opartych na tych łukach różnią się o 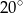 . Wynika stąd, że większy z tych katów ma miarę
. Wynika stąd, że większy z tych katów ma miarę
A) 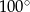 B)
B) 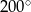 C)
C) 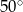 D)
D) 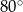
Dany jest okrąg o środku 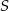 i promieniu
i promieniu  , długość łuku
, długość łuku 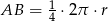 (patrz rysunek).
(patrz rysunek).
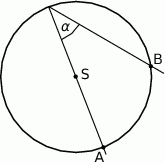
Miara kąta  jest równa
jest równa
A) 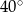 B)
B) 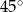 C)
C) 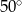 D)
D) 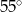
Dany jest okrąg o środku 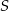 i promieniu
i promieniu  , długość łuku
, długość łuku 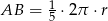 (patrz rysunek).
(patrz rysunek).
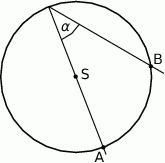
Miara kąta  jest równa
jest równa
A) 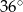 B)
B) 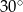 C)
C) 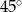 D)
D) 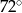
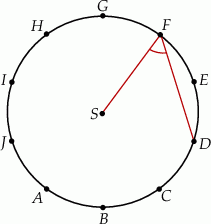
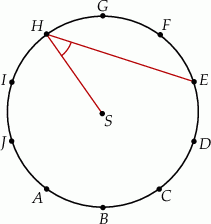
Punkty 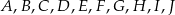 dzielą okrąg o środku
dzielą okrąg o środku 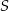 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 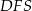 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 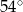 B)
B) 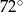 C)
C) 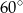 D)
D) 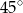
Punkty 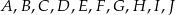 dzielą okrąg o środku
dzielą okrąg o środku 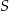 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 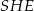 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 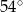 B)
B) 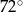 C)
C) 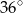 D)
D) 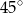
Odcinek 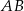 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 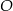 i promieniu
i promieniu  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 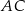 ma długość
ma długość 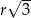 , więc
, więc
A) 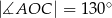 B)
B) 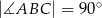 C)
C) 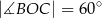 D)
D) 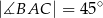
Trójkąty 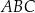 i
i 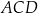 są wpisane w okrąg o środku
są wpisane w okrąg o środku 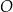 . Odcinek
. Odcinek 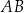 jest średnicą okręgu.
jest średnicą okręgu.

Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 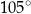 B)
B) 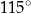 C)
C) 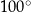 D)
D) 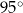
Trójkąty 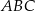 i
i 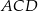 są wpisane w okrąg o środku
są wpisane w okrąg o środku 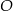 . Odcinek
. Odcinek 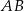 jest średnicą okręgu.
jest średnicą okręgu.
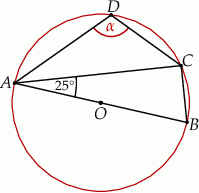
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 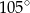 B)
B) 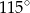 C)
C) 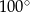 D)
D) 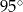
Trójkąty 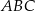 i
i 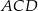 są wpisane w okrąg o środku
są wpisane w okrąg o środku 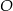 . Odcinek
. Odcinek 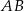 jest średnicą okręgu.
jest średnicą okręgu.
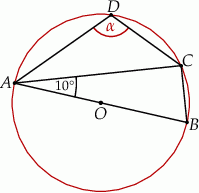
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 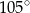 B)
B) 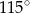 C)
C) 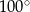 D)
D) 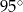
Punkty 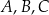 leżą na okręgu o środku
leżą na okręgu o środku 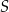 . Punkt
. Punkt 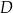 jest punktem przecięcia cięciwy
jest punktem przecięcia cięciwy 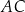 i średnicy okręgu poprowadzonej z punktu
i średnicy okręgu poprowadzonej z punktu 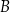 . Miara kąta
. Miara kąta 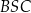 jest równa
jest równa  , a miara kąta
, a miara kąta 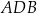 jest równa
jest równa 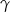 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 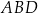 ma miarę
ma miarę
A) 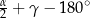 B)
B) 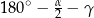 C)
C) 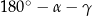 D)
D) 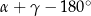
Punkty 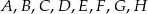 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 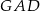 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
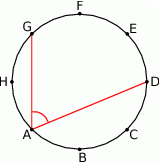
A) 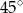 B)
B) 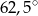 C)
C) 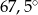 D)
D) 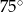
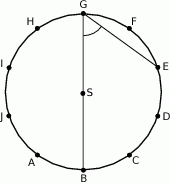
Punkty 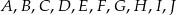 dzielą okrąg o środku
dzielą okrąg o środku 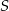 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 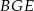 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 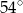 B)
B) 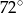 C)
C) 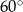 D)
D) 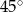
Punkty 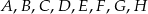 dzielą okrąg na 8 równych łuków. Miara kąta
dzielą okrąg na 8 równych łuków. Miara kąta 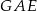 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
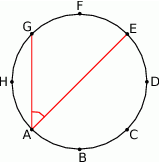
A) 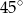 B)
B) 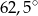 C)
C) 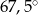 D)
D) 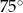
Punkty 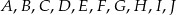 dzielą okrąg o środku
dzielą okrąg o środku 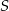 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 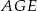 zaznaczonego na rysunku.
zaznaczonego na rysunku.
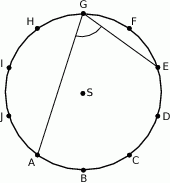
A) 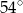 B)
B) 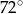 C)
C) 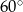 D)
D) 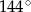
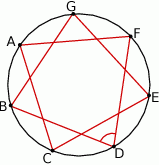
Punkty 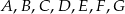 okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 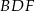 jest równa
jest równa
A) 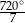 B)
B) 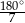 C)
C) 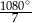 D)
D) 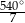
Punkty 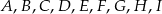 dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 9 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 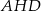 jest równa
jest równa
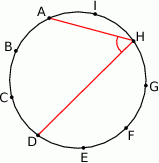
A) 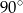 B)
B) 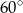 C)
C) 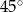 D)
D) 
Punkt 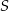 jest środkiem okręgu.
jest środkiem okręgu.
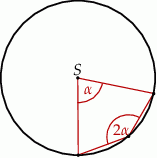
Miara kąta środkowego  jest równa
jest równa
A) 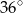 B)
B) 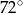 C)
C) 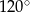 D)
D) 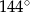
Trójkąt 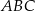 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 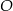 . Miara kąta
. Miara kąta 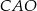 jest równa
jest równa 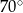 (zobacz rysunek).
(zobacz rysunek).
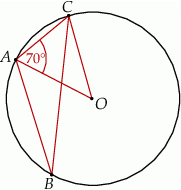
Wtedy miara kąta 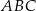 jest równa
jest równa
A) 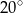 B)
B) 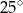 C)
C) 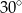 D)
D) 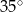
Bok 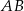 trójkąta
trójkąta 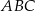 jest średnicą okręgu o środku
jest średnicą okręgu o środku 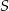 , a boki
, a boki 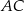 i
i 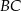 przecinają ten okrąg odpowiednio w punktach
przecinają ten okrąg odpowiednio w punktach 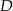 i
i 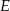 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 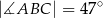 i
i 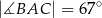 .
.
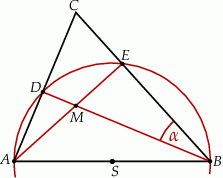
Zaznaczony na rysunku kąt  jest równy
jest równy
A) 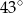 B)
B) 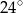 C)
C) 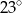 D)
D) 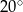
Punkt 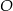 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 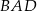 ma miarę
ma miarę
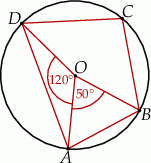
A) 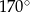 B)
B) 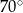 C)
C) 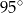 D)
D) 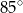
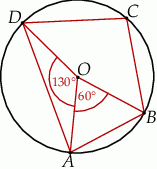
Punkt 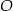 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany 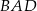 ma miarę
ma miarę
A) 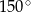 B)
B) 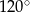 C)
C) 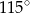 D)
D) 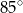
Kąt środkowy oparty na łuku, którego długość jest równa 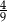 długości okręgu, ma miarę
długości okręgu, ma miarę
A) 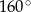 B)
B) 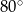 C)
C) 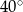 D)
D) 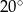
Kąt środkowy oparty na łuku, którego długość jest równa  długości okręgu, ma miarę
długości okręgu, ma miarę
A) 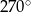 B)
B) 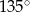 C)
C) 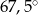 D)
D) 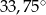
W okręgu o środku w punkcie 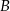 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 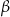 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 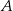 i
i 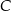 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 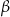 znajduje się w punkcie
znajduje się w punkcie 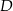 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 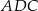 jest równoboczny B)
jest równoboczny B) 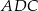 jest prostokątny
jest prostokątny
C) 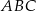 jest równoboczny D)
jest równoboczny D) 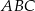 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 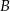 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 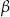 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 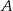 i
i 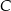 leżące na okręgu. Różnica miar tych kątów jest równa
leżące na okręgu. Różnica miar tych kątów jest równa 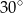 . Wierzchołek kąta
. Wierzchołek kąta 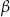 znajduje się w punkcie
znajduje się w punkcie 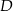 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 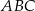 jest równoboczny B)
jest równoboczny B) 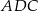 jest prostokątny
jest prostokątny
C) 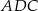 jest równoboczny D)
jest równoboczny D) 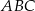 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 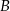 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 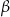 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 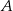 i
i 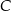 leżące na okręgu. Suma miar tych kątów jest równa
leżące na okręgu. Suma miar tych kątów jest równa 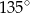 . Wierzchołek kąta
. Wierzchołek kąta 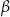 znajduje się w punkcie
znajduje się w punkcie 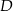 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 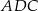 jest równoboczny B)
jest równoboczny B) 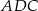 jest prostokątny
jest prostokątny
C) 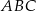 jest równoboczny D)
jest równoboczny D) 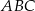 jest prostokątny
jest prostokątny
