Punkty 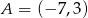 i
i 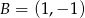 są wierzchołkami pięciokąta foremnego
są wierzchołkami pięciokąta foremnego 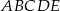 . Obwód tego pięciokąta jest równy
. Obwód tego pięciokąta jest równy
A) 50 B) 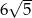 C) 60 D)
C) 60 D) 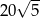
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Różne
Punkty 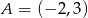 i
i 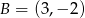 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 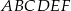 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 50 B) 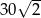 C) 300 D)
C) 300 D) 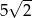
Dane są punkty 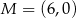 ,
, 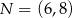 oraz
oraz 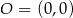 . Tangens kąta ostrego
. Tangens kąta ostrego 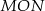 jest równy
jest równy
A) 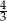 B)
B) 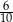 C)
C)  D)
D) 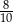
Dane są punkty 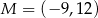 ,
, 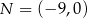 oraz
oraz 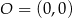 . Tangens kąta ostrego
. Tangens kąta ostrego 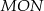 jest równy
jest równy
A) 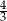 B)
B) 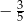 C)
C)  D)
D) 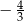
Punkt 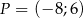 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  (w standardowym położeniu w układzie współrzędnych). Zatem
(w standardowym położeniu w układzie współrzędnych). Zatem 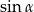 jest równy
jest równy
A) 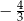 B)
B) 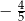 C)
C) 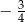 D)
D) 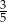
Do prostej należy początek układu współrzędnych oraz punkt 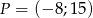 . Wówczas cosinus kąta nachylenia tej prostej do osi
. Wówczas cosinus kąta nachylenia tej prostej do osi 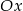 jest równy
jest równy
A) 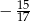 B)
B) 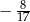 C)
C) 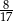 D)
D) 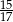
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 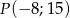 .
.
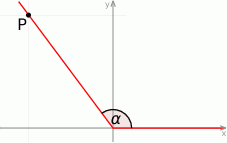
Zatem 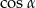 jest równy
jest równy
A) 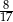 B)
B) 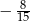 C)
C) 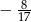 D)
D) 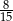
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 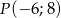 .
.
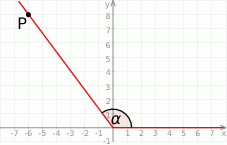
Zatem 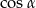 jest równy
jest równy
A) 0,8 B) 0,6 C) 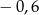 D)
D) 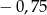
Punkt 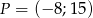 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  . Wówczas
. Wówczas
A) 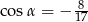 B)
B) 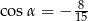 C)
C) 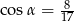 D)
D) 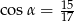
Równanie 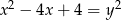 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę B) okrąg C) punkt D) dwie proste
Pole figury ograniczonej prostymi 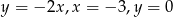 i
i 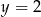 jest równe
jest równe
A) 9 B) 18 C) 5 D) 19
Pole figury ograniczonej prostymi 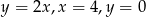 i
i 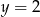 jest równe
jest równe
A) 9 B) 14 C) 5 D) 7
Pole figury ograniczonej prostymi 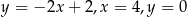 i
i 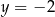 jest równe
jest równe
A) 5 B) 10 C) 7 D) 4
Dane są punkty 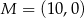 ,
, 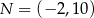 oraz
oraz 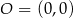 . Tangens kąta rozwartego
. Tangens kąta rozwartego 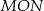 jest równy
jest równy
A) 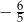 B)
B) 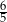 C) 1 D)
C) 1 D) 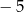
Odległość punktu 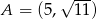 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 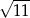 C)
C) 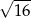 D) 5
D) 5
Odległość punktu 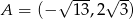 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 1 C) 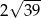 D) 5
D) 5
Odległość punktu 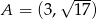 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 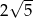 C)
C) 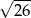 D) 5
D) 5
Każdy kąt wewnętrzny sześciokąta 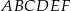 ma miarę
ma miarę 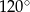 . Bok
. Bok 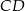 tego sześciokąta jest zwarty w prostej o równaniu
tego sześciokąta jest zwarty w prostej o równaniu 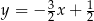 , a punkt
, a punkt 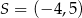 jest środkiem boku
jest środkiem boku 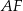 . Bok
. Bok 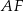 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu
A) 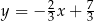 B)
B) 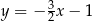 C)
C) 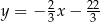 D)
D) 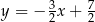
Dane są punkty o współrzędnych 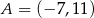 oraz
oraz 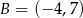 . Średnica okręgu wpisanego w sześciokąt foremny o boku
. Średnica okręgu wpisanego w sześciokąt foremny o boku 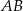 jest równa
jest równa
A) 10 B) 5 C) 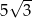 D)
D) 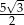
Suma odległości punktu 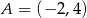 od prostych o równaniach
od prostych o równaniach 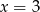 i
i 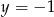 jest równa
jest równa
A) 10 B) 9 C) 8 D) 7
Przekątne 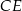 i
i 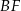 sześciokąta foremnego
sześciokąta foremnego 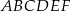 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 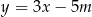 i
i 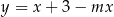 . Zatem
. Zatem
A) 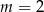 B)
B) 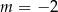 C)
C) 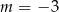 D)
D) 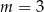
W układzie współrzędnych na płaszczyźnie dany jest punkt 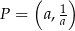 , gdzie
, gdzie  jest pewną liczbą niezerową. Punkt
jest pewną liczbą niezerową. Punkt 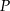 może należeć do tej samej ćwiartki układu współrzędnych, co punkt
może należeć do tej samej ćwiartki układu współrzędnych, co punkt
A) 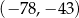 B)
B) 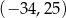 C)
C) 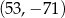 D)
D) 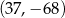
Punkty 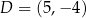 i
i 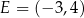 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego  . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 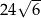 B)
B) 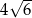 C)
C) 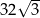 D)
D) 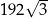
W kartezjańskim układzie współrzędnych dane są punkty: 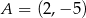 ,
, 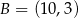 i
i 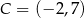 . Punkty
. Punkty 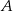 ,
, 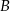 i
i 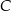
| A) | są współliniowe, |
| B) | są wierzchołkami trójkąta prostokątnego, |
| C) | są wierzchołkami trójkąta równoramiennego, |
ponieważ
1) 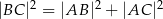 , , | 2) 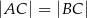 , , | 3) 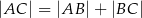 , , |
W układzie współrzędnych na płaszczyźnie danych jest 5 punktów: 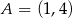 ,
, 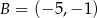 ,
, 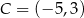 ,
, 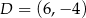 ,
, 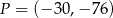 . Punkt
. Punkt 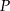 należy do tej samej ćwiartki układu współrzędnych co punkt
należy do tej samej ćwiartki układu współrzędnych co punkt
A) 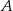 B)
B) 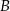 C)
C) 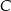 D)
D) 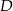
W układzie współrzędnych na płaszczyźnie danych jest 5 punktów: 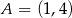 ,
, 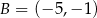 ,
, 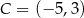 ,
, 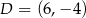 ,
, 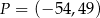 . Punkt
. Punkt 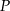 należy do tej samej ćwiartki układu współrzędnych co punkt
należy do tej samej ćwiartki układu współrzędnych co punkt
A) 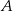 B)
B) 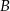 C)
C) 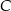 D)
D) 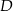
Punkt 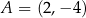 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 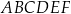 wpisanego w okrąg o środku
wpisanego w okrąg o środku 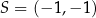 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 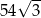 B)
B) 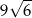 C)
C) 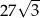 D)
D) 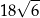
Punkt 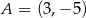 jest wierzchołkiem sześciokąta foremnego
jest wierzchołkiem sześciokąta foremnego 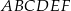 wpisanego w okrąg o środku
wpisanego w okrąg o środku 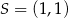 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 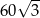 B)
B) 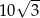 C)
C) 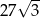 D)
D) 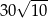
Nierówność 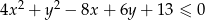 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) okrąg B) koło C) punkt D) zbiór pusty
Nierówność 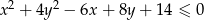 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) okrąg B) koło C) punkt D) zbiór pusty
Nierówność 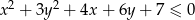 przedstawia na płaszczyźnie
przedstawia na płaszczyźnie
A) punkt B) koło C) okrąg D) zbiór pusty
Równanie 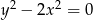 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę
B) dwie proste równoległe
C) dwie proste prostopadłe
D) dwie proste przecinające się pod kątem innym niż prosty
Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 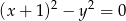 , jest
, jest
A) parabolą B) prostą C) okręgiem D) sumą dwóch prostych
Zbiór punktów płaszczyzny, których współrzędne spełniają równanie 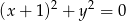 , jest
, jest
A) parabolą B) punktem C) okręgiem D) sumą dwóch prostych

