Ciąg arytmetyczny 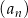 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 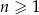 . Różnica tego ciągu jest równa 2. Wtedy
. Różnica tego ciągu jest równa 2. Wtedy
A) 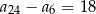 B)
B) 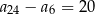 C)
C) 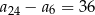 D)
D) 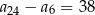
/Szkoła średnia/Zadania testowe/Ciągi
Ciąg arytmetyczny 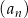 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 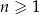 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa 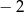 . Wtedy
. Wtedy
A) 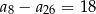 B)
B) 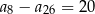 C)
C) 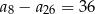 D)
D) 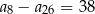
Ciąg 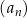 jest określony wzorem
jest określony wzorem 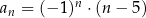 dla każdej liczby naturalnej
dla każdej liczby naturalnej 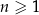 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwszy wyraz ciągu 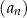 jest dwa razy większy od trzeciego wyrazu tego ciągu. jest dwa razy większy od trzeciego wyrazu tego ciągu. | P | F |
Wszystkie wyrazy ciągu 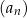 są dodatnie. są dodatnie. | P | F |
Trzywyrazowy ciąg 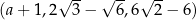 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 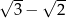 B)
B) 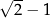 C)
C) 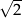 D)
D) 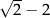
W ciągu arytmetycznym 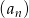 , określonym dla
, określonym dla 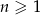 , dane są dwa wyrazy:
, dane są dwa wyrazy: 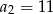 i
i 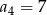 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 36 B) 40 C) 13 D) 20
W ciągu arytmetycznym 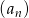 , określonym dla
, określonym dla 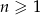 , dane są dwa wyrazy:
, dane są dwa wyrazy: 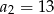 i
i 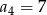 . Suma czterech początkowych wyrazów tego ciągu jest równa
. Suma czterech początkowych wyrazów tego ciągu jest równa
A) 92 B) 39 C) 46 D) 50
Dany jest ciąg 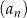 określony wzorem
określony wzorem 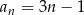 dla każdej liczby naturalnej
dla każdej liczby naturalnej 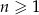 . Ciąg
. Ciąg 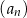 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 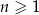
1) 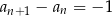 , , | 2) 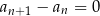 , , | 3) 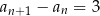 , , |
Dany jest ciąg 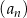 określony wzorem
określony wzorem 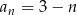 dla każdej liczby naturalnej
dla każdej liczby naturalnej 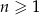 . Ciąg
. Ciąg 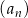 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 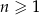
1) 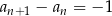 , , | 2) 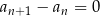 , , | 3) 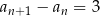 , , |
Liczby 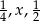 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 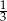 B)
B)  C)
C) 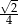 D)
D) 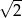
Liczby 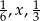 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 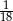 B)
B) 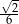 C)
C) 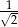 D)
D) 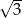
Trzywyrazowy ciąg 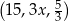 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 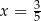 B)
B) 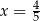 C)
C) 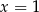 D)
D) 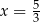
Trójwyrazowy ciąg 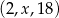 jest rosnącym ciągiem geometrycznym. Wtedy
jest rosnącym ciągiem geometrycznym. Wtedy
A) 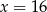 B)
B) 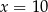 C)
C) 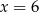 D)
D) 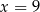
Liczby 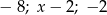 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  może być równa
może być równa
A) 4 B) 6 C) 7 D) 8
Trzywyrazowy ciąg 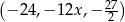 jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są ujemne. Stąd wynika, że
A) 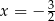 B)
B) 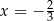 C)
C) 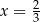 D)
D) 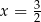
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 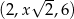 . Wówczas
. Wówczas
A) 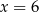 B)
B) 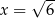 C)
C) 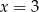 D)
D) 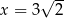
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 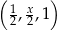 . Wówczas
. Wówczas
A) 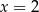 B)
B) 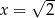 C)
C) 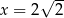 D)
D) 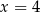
Jeżeli liczby 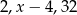 tworzą rosnący ciąg geometryczny, to
tworzą rosnący ciąg geometryczny, to
A) 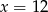 B)
B) 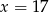 C)
C) 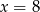 D)
D) 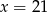
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 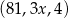 . Stąd wynika, że
. Stąd wynika, że
A) 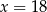 B)
B) 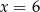 C)
C) 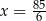 D)
D) 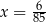
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 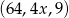 . Stąd wynika, że
. Stąd wynika, że
A) 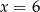 B)
B) 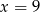 C)
C) 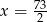 D)
D) 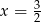
Liczby 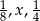 tworzą rosnący ciąg geometryczny. Liczba
tworzą rosnący ciąg geometryczny. Liczba  może być równa
może być równa
A) 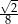 B)
B) 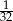 C)
C) 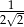 D)
D) 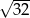
Liczby 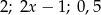 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem monotonicznego ciągu geometrycznego dla
A) 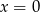 B)
B) 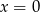 lub
lub 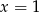 C)
C) 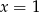 D)
D) 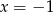
Ciąg 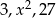 jest ciągiem geometrycznym, gdy
jest ciągiem geometrycznym, gdy
A) tylko 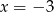 B) tylko
B) tylko 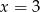 C)
C) 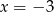 lub
lub 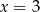 D)
D) 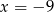 lub
lub 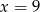
Ciąg 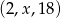 jest ciągiem geometrycznym tylko wtedy, gdy
jest ciągiem geometrycznym tylko wtedy, gdy
A) 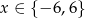 B)
B) 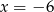 C)
C) 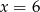 D)
D) 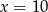
W rosnącym ciągu geometrycznym stosunek wyrazu czwartego do drugiego jest równy 8. Iloraz tego ciągu jest równy
A) 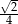 B) 4 C)
B) 4 C) 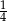 D)
D) 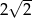
Dany jest ciąg geometryczny 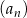 , określony dla
, określony dla 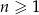 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 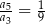 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 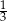 B)
B) 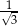 C) 3 D)
C) 3 D) 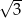
Dany jest ciąg geometryczny 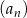 , określony dla
, określony dla 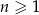 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 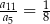 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 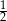 B)
B) 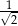 C)
C) 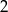 D)
D) 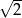
Dany jest ciąg 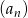 określony wzorem
określony wzorem 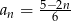 dla
dla 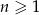 . Ciąg ten jest
. Ciąg ten jest
A) arytmetyczny i jego różnica jest równa 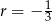 .
.
B) arytmetyczny i jego różnica jest równa 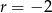 .
.
C) geometryczny i jego iloraz jest równy 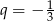 .
.
D) geometryczny i jego iloraz jest równy 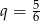 .
.
Dany jest ciąg 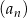 określony wzorem
określony wzorem 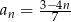 dla
dla 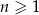 . Ciąg ten jest
. Ciąg ten jest
A) geometryczny i jego iloraz jest równy 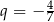 .
.
B) geometryczny i jego iloraz jest równy 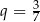 .
.
C) arytmetyczny i jego różnica jest równa 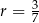 .
.
D) arytmetyczny i jego różnica jest równa 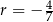 .
.
W ciągu arytmetycznym 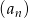 dane są
dane są 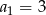 i
i 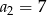 . Wtedy suma
. Wtedy suma 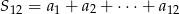 jest równa
jest równa
A) 324 B) 300 C) 282 D) 306
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 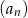 , w którym
, w którym 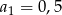 oraz
oraz 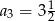 jest równa
jest równa
A) 295 B) 298 C) 305 D) 308
Ciąg 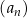 określony wzorem
określony wzorem 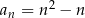 dla każdej liczby naturalnej
dla każdej liczby naturalnej 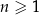 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 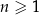
1) różnica 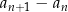 jest liczbą ujemną. jest liczbą ujemną. |
2) różnica 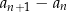 jest równa zero. jest równa zero. |
3) różnica 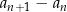 jest liczbą dodatnią. jest liczbą dodatnią. |
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 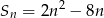 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 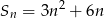 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -6 B) 14 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 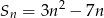 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 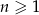 , wyraża się wzorem
, wyraża się wzorem 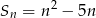 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) -5 B) -3 C) 1 D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 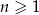 , wyraża się wzorem
, wyraża się wzorem 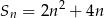 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 4 B) 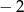 C)
C) 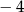 D) 2
D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 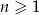 , wyraża się wzorem
, wyraża się wzorem 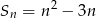 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 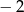 B)
B) 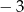 C) 2 D) 1
C) 2 D) 1
Suma
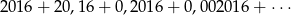
wszystkich wyrazów nieskończonego ciągu liczb rzeczywistych jest równa
A) 201600 B) 2240 C) 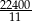 D)
D) 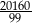
Suma
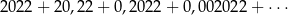
wszystkich wyrazów nieskończonego ciągu geometrycznego liczb rzeczywistych jest równa
A) 202200 B) 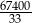 C) 67400 D)
C) 67400 D) 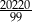
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a różnica tego ciągu jest równa 3. Suma 100 początkowych wyrazów tego ciągu o numerach parzystych jest równa
A) 15100 B) 30500 C) 30200 D) 61000
W ciągu geometrycznym 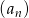 dane są
dane są 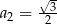 i
i 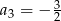 . Wtedy wyraz
. Wtedy wyraz 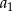 jest równy
jest równy
A) 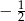 B)
B) 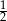 C)
C) 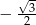 D)
D) 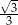
W ciągu geometrycznym 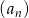 dane są
dane są 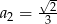 i
i 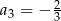 . Wtedy wyraz
. Wtedy wyraz 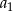 jest równy
jest równy
A) 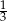 B)
B) 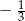 C)
C) 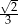 D)
D) 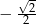
Który wyraz ciągu 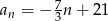 jest równy zero?
jest równy zero?
A) 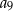 B)
B) 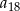 C)
C) 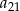 D)
D) 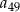
Granica 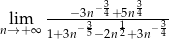 jest równa
jest równa
A) 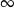 B)
B) 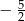 C) 0 D)
C) 0 D) 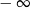
Piąty wyraz ciągu 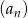 określonego wzorem
określonego wzorem 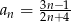 , gdzie
, gdzie 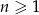 jest równy
jest równy
A) 1 B) 5 C) 10 D) 0,5
Szósty wyraz ciągu 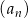 określonego wzorem
określonego wzorem 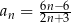 , gdzie
, gdzie 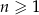 jest równy
jest równy
A) 2 B) 1 C) 12 D) 0,5
Ciąg 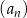 jest określony wzorem
jest określony wzorem 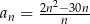 dla każdej liczby naturalnej
dla każdej liczby naturalnej 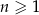 . Wtedy
. Wtedy 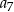 jest równy
jest równy
A) 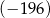 B)
B) 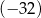 C)
C) 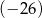 D)
D) 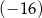
Ciąg 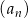 jest określony wzorem
jest określony wzorem 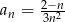 dla każdej liczby naturalnej
dla każdej liczby naturalnej 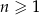 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 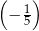 B)
B) 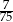 C)
C) 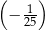 D)
D) 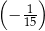
Piąty wyraz ciągu 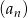 określonego wzorem
określonego wzorem 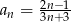 , gdzie
, gdzie 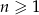 jest równy
jest równy
A) 1 B) 5 C) 10 D) 0,5
Ciąg 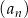 jest określony wzorem
jest określony wzorem 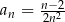 dla każdej liczby naturalnej
dla każdej liczby naturalnej 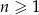 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy
A) 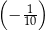 B)
B) 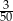 C)
C) 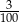 D)
D) 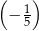
Nieskończony ciąg liczbowy jest określony wzorem 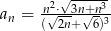 dla
dla 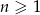 . Wtedy
. Wtedy
A) 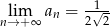 B)
B) 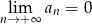 C)
C) 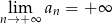 D)
D) 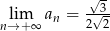
Dany jest ciąg geometryczny 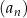 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 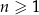 . Pierwszy wyraz tego ciągu jest równy 288, natomiast iloraz ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy 288, natomiast iloraz ciągu jest równy 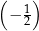 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wśród wyrazów ciągu 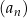 jest dokładnie 5 liczb całkowitych. jest dokładnie 5 liczb całkowitych. | P | F |
Jeden z wyrazów ciągu 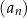 jest równy jest równy 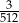 . . | P | F |
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 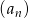 danego wzorem
danego wzorem 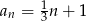 jest równa
jest równa
A) 370 B) 185 C) 11 D) 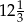
Ciąg arytmetyczny 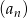 jest określony wzorem
jest określony wzorem 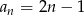 , dla
, dla 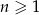 . Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
A) 9900 B) 9950 C) 10000 D) 10050
Suma dziesięciu początkowych wyrazów nieskończonego ciągu arytmetycznego 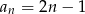 wynosi
wynosi
A) 80 B) 90 C) 110 D) 100
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 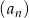 danego wzorem
danego wzorem 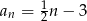 jest równa
jest równa
A) 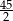 B)
B) 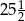 C) 45 D)
C) 45 D) 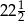
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 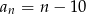 wynosi
wynosi
A) 8 B) 9 C) 10 D) 11
Suma dwudziestu początkowych wyrazów ciągu arytmetycznego 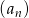 danego wzorem
danego wzorem 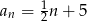 jest równa
jest równa
A) 205 B) 410 C) 200 D) 210

