Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 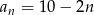 , gdzie
, gdzie 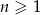 jest równa 14. Zatem
jest równa 14. Zatem
A) 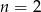 B) liczba
B) liczba 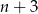 dzieli się przez 5 C)
dzieli się przez 5 C) 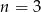 D)
D) 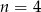
/Szkoła średnia/Zadania testowe/Ciągi/Arytmetyczny/Dana suma
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 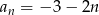 , gdzie
, gdzie 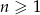 jest równa
jest równa 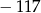 . Zatem
. Zatem
A) 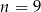 B)
B) 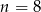 C)
C) 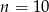 D)
D) 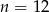
Suma dwóch początkowych wyrazów ciągu arytmetycznego 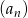 wynosi 5, a trzeci wyraz jest równy 7. Wówczas
wynosi 5, a trzeci wyraz jest równy 7. Wówczas
A) 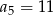 B)
B) 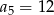 C)
C) 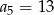 D)
D) 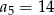
Suma dwóch początkowych wyrazów ciągu arytmetycznego 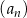 wynosi 7, a trzeci wyraz jest równy 5. Wówczas
wynosi 7, a trzeci wyraz jest równy 5. Wówczas
A) 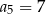 B)
B) 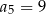 C)
C) 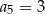 D)
D) 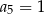
Suma ciągu arytmetycznego jest określona wzorem 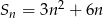 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 24 B) 15 C) 6 D) 2
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 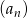 wyraża się wzorem
wyraża się wzorem 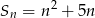 (
(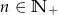 ). Drugi wyraz ciągu
). Drugi wyraz ciągu 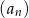 jest równy
jest równy
A) 2 B) 8 C) 12 D) 14
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 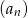 jest określona wzorem
jest określona wzorem 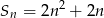 . Wtedy wyraz
. Wtedy wyraz 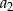 jest równy
jest równy
A) 4 B) 8 C) 12 D) 24
Jeżeli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 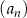 określona jest wzorem
określona jest wzorem 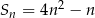 , to wartość piątego wyrazu tego ciągu jest równa
, to wartość piątego wyrazu tego ciągu jest równa
A) 33 B) 35 C) 60 D) 95
Suma ciągu arytmetycznego jest określona wzorem 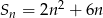 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 20 B) 16 C) 12 D) 8
Suma częściowa ciągu arytmetycznego jest wyrażona wzorem 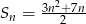 . Wobec tego:
. Wobec tego:
A) 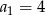 B)
B) 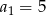 C)
C) 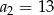 D)
D) 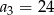
Jeśli suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 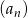 określona jest wzorem
określona jest wzorem 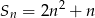 , to wartość trzeciego wyrazu tego ciągu jest równa
, to wartość trzeciego wyrazu tego ciągu jest równa
A) 8 B) 10 C) 11 D) 21
Dla każdej liczby całkowitej dodatniej  suma
suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 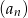 jest określona wzorem
jest określona wzorem 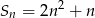 . Wtedy wyraz
. Wtedy wyraz 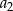 jest równy
jest równy
A) 3 B) 6 C) 7 D) 10
Suma ciągu arytmetycznego jest określona wzorem 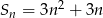 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 18 B) 3 C) 12 D) 15
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 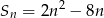 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 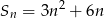 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -6 B) 14 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego wyraża się wzorem
początkowych wyrazów ciągu arytmetycznego wyraża się wzorem 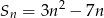 . Wynika stąd, że różnica ciągu jest równa
. Wynika stąd, że różnica ciągu jest równa
A) -8 B) 4 C) 6 D) 8
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 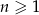 , wyraża się wzorem
, wyraża się wzorem 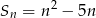 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) -5 B) -3 C) 1 D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 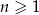 , wyraża się wzorem
, wyraża się wzorem 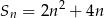 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 4 B) 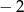 C)
C) 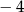 D) 2
D) 2
Suma  początkowych wyrazów ciągu arytmetycznego, gdzie
początkowych wyrazów ciągu arytmetycznego, gdzie 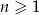 , wyraża się wzorem
, wyraża się wzorem 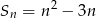 . Wobec tego różnica tego ciągu wynosi
. Wobec tego różnica tego ciągu wynosi
A) 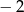 B)
B) 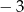 C) 2 D) 1
C) 2 D) 1
W ciągu arytmetycznym mamy 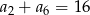 . Oblicz
. Oblicz 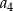 .
.
A) 8 B) 16 C) 4 D) 12
Ciąg arytmetyczny 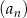 , określony dla
, określony dla 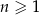 , spełnia warunek
, spełnia warunek 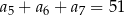 . Wtedy
. Wtedy
A) 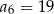 B)
B) 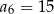 C)
C) 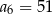 D)
D) 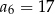
Ciąg arytmetyczny 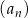 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 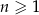 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 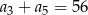 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Ciąg arytmetyczny 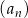 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 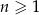 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 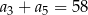 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
W ciągu arytmetycznym 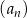 , określonym dla
, określonym dla 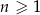 , spełniony jest warunek
, spełniony jest warunek 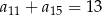 . Wtedy
. Wtedy
A) 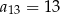 B)
B) 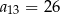 C)
C) 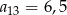 D)
D) 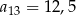
Dla ciągu arytmetycznego 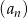 , określonego dla
, określonego dla 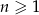 , spełniony jest warunek
, spełniony jest warunek 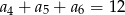 . Wtedy
. Wtedy
A) 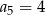 B)
B) 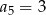 C)
C) 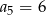 D)
D) 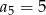
Ciąg arytmetyczny 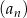 , określony dla
, określony dla 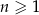 , spełnia warunek
, spełnia warunek 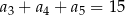 . Wtedy
. Wtedy
A) 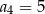 B)
B) 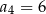 C)
C) 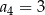 D)
D) 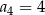
W ciągu arytmetycznym 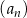 , określonym dla
, określonym dla 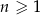 , spełniony jest warunek
, spełniony jest warunek 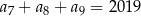 . Suma
. Suma 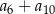 jest równa
jest równa
A) 673 B) 1346 C) 1009,5 D) 2019
Wszystkie wyrazy rosnącego ciągu arytmetycznego 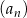 , gdzie
, gdzie 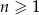 są dodatnimi liczbami całkowitymi. Jeżeli
są dodatnimi liczbami całkowitymi. Jeżeli 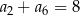 , to suma dziesięciu początkowych wyrazów ciągu
, to suma dziesięciu początkowych wyrazów ciągu 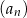 jest równa
jest równa
A) 45 B) 66 C) 55 D) 48
Ciąg arytmetyczny 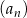 , określony dla
, określony dla 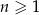 , spełnia warunek
, spełnia warunek 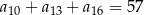 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 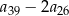 jest równa
jest równa
A) 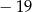 B)
B) 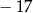 C) 13 D)
C) 13 D) 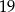
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 18. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 4 D) 3
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 21. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 4 D) 7
Trzy liczby tworzą ciąg arytmetyczny. Suma tych liczb jest równa 24. Drugi wyraz tego ciągu jest równy
A) 6 B) 5 C) 8 D) 7
W ciągu arytmetycznym 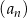 dane są
dane są 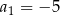 ,
, 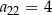 i
i 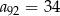 . Wtedy suma
. Wtedy suma
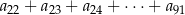
jest równa
A) 1293 B) 1315 C) 1311 D) 1345
Suma dziesięciu początkowych wyrazów ciągu arytmetycznego 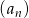 jest równa 35. Pierwszy wyraz
jest równa 35. Pierwszy wyraz 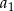 tego ciągu jest równy 3. Wtedy
tego ciągu jest równy 3. Wtedy
A) 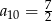 B)
B) 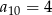 C)
C) 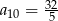 D)
D) 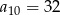
Suma dwunastu początkowych wyrazów ciągu arytmetycznego 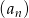 jest równa 42. Pierwszy wyraz
jest równa 42. Pierwszy wyraz 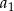 tego ciągu jest równy 4. Wtedy
tego ciągu jest równy 4. Wtedy
A) 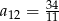 B)
B) 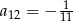 C)
C) 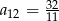 D)
D) 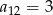
Suma pierwszego i szóstego wyrazu pewnego ciągu arytmetycznego jest równa 13 . Wynika stąd, że suma trzeciego i czwartego wyrazu tego ciągu jest równa
A) 13 B) 12 C) 7 D) 6
Suma pierwszego i siódmego wyrazu pewnego ciągu arytmetycznego jest równa 17 . Wynika stąd, że suma trzeciego i piątego wyrazu tego ciągu jest równa
A) 7 B) 16 C) 17 D) 6
W ciągu arytmetycznym 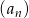 , określonym dla
, określonym dla 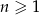 , spełniony jest warunek
, spełniony jest warunek 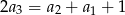 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 0 B) 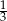 C)
C) 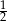 D) 1
D) 1
W ciągu arytmetycznym 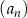 , określonym dla
, określonym dla 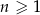 , spełniony jest warunek
, spełniony jest warunek 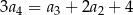 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 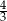 B) 1 C)
B) 1 C)  D)
D) 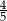
W ciągu arytmetycznym 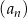 , określonym dla
, określonym dla 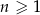 , spełniony jest warunek
, spełniony jest warunek 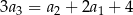 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 4 B) 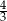 C) 2 D)
C) 2 D) 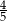
W ciągu arytmetycznym 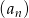 , określonym dla
, określonym dla 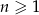 , spełniony jest warunek
, spełniony jest warunek 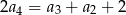 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 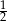 B) 1 C)
B) 1 C)  D) 0
D) 0
W ciągu arytmetycznym 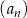 , określonym dla
, określonym dla 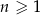 , spełniony jest warunek
, spełniony jest warunek 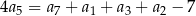 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 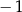 B)
B) 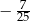 C)
C) 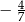 D) 2
D) 2
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a suma jego pięciu początkowych wyrazów wynosi 55. Czwarty wyraz tego ciągu jest równy
A) 12 B) 13 C) 14 D) 15
Pierwszy wyraz ciągu arytmetycznego wynosi 7, suma siedmiu początkowych wyrazów ciągu jest równa 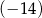 . Czwarty wyraz ciągu jest równy
. Czwarty wyraz ciągu jest równy
A) 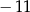 B)
B) 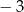 C)
C) 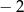 D) 16
D) 16
Suma dwudziestu początkowych wyrazów pewnego ciągu arytmetycznego jest 6 razy większa od sumy dziesięciu początkowych wyrazów tego ciągu. Wynika stąd, że suma drugiego i czwartego wyrazu tego ciągu jest równa
A) 0 B) 2 C) 8 D) 6
W ciągu arytmetycznym 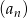 dla
dla 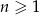 ,
, 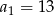 oraz
oraz 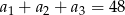 . Wtedy suma
. Wtedy suma 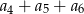 jest równa
jest równa
A) 48 B) 96 C) 75 D) 58

