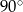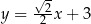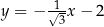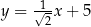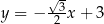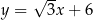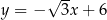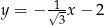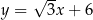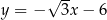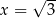Prosta o równaniu 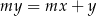 nie przecina prostej
nie przecina prostej 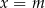 . Zatem
. Zatem
A) 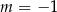 B)
B) 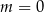 C)
C) 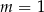 D)
D) 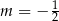
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej/Wzajemne położenie prostych
Równania 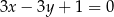 i
i 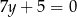 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe B) są równoległe
C) przecinają się pod kątem 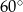 D) przecinają się pod kątem
D) przecinają się pod kątem 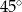
Równania 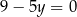 i
i 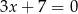 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe B) są równoległe
C) przecinają się pod kątem 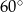 D) przecinają się pod kątem
D) przecinają się pod kątem 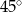
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 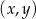 , dane są proste
, dane są proste 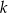 oraz
oraz 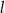 o równaniach
o równaniach
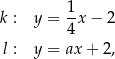
gdzie  jest pewną liczbą rzeczywistą. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest pewną liczbą rzeczywistą. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 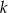 i i 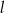 mogą mięc nieskończenie wiele punktów wspólnych. mogą mięc nieskończenie wiele punktów wspólnych. | P | F |
Punkt wspólny prostych 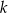 i i 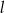 może leżeć w I ćwiartce układu współrzędnych może leżeć w I ćwiartce układu współrzędnych | P | F |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 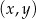 , dane są:
, dane są:
– prosta 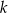 o równaniu
o równaniu 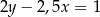
– prosta 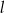 o równaniu
o równaniu 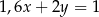 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 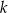 i i 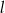 przecinają się pod kątem przecinają się pod kątem 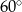 . . | P | F |
Punkt wspólny prostych 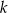 i i 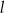 ma obie współrzędne całkowite. ma obie współrzędne całkowite. | P | F |
Proste o równaniach 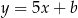 i
i 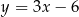 przecinają się w punkcie leżącym na osi
przecinają się w punkcie leżącym na osi 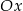 . Zatem
. Zatem
A) 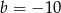 B)
B) 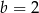 C)
C) 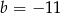 D)
D) 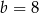
Proste o równaniach 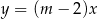 oraz
oraz 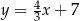 przecinają się w jednym punkcie Wtedy
przecinają się w jednym punkcie Wtedy
A) 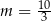 B)
B) 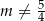 C)
C) 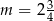 D)
D) 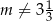
Prosta 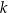 przechodzi przez punkty
przechodzi przez punkty 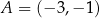 i
i 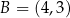 , a prosta
, a prosta 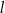 opisana jest równaniem
opisana jest równaniem 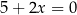 . Tangens kąta ostrego pod jakim przecinają się proste
. Tangens kąta ostrego pod jakim przecinają się proste 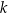 i
i 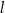 jest równy
jest równy
A) 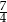 B)
B) 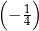 C)
C) 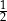 D)
D) 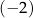
Proste o równaniach 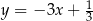 oraz
oraz 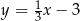 przecinają się w punkcie
przecinają się w punkcie 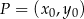 . Wynika stąd, że
. Wynika stąd, że
A) 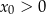 i
i 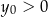 B)
B) 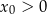 i
i 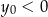 C)
C) 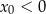 i
i 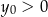 D)
D) 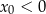 i
i 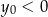
W kartezjańskim układzie współrzędnych 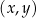 , punkt
, punkt 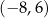 jest punktem przecięcia prostych o równaniach
jest punktem przecięcia prostych o równaniach
A) 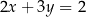 i
i 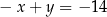 B)
B) 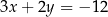 i
i 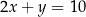
C) 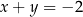 i
i 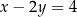 D)
D) 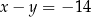 i
i 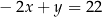
W kartezjańskim układzie współrzędnych 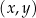 , punkt
, punkt 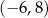 jest punktem przecięcia prostych o równaniach
jest punktem przecięcia prostych o równaniach
A) 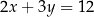 i
i 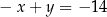 B)
B) 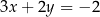 i
i 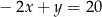
C) 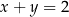 i
i 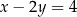 D)
D) 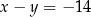 i
i 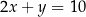
Proste o równaniach 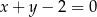 i
i 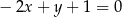 przecinają się w punkcie o współrzędnych
przecinają się w punkcie o współrzędnych
A) 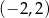 B)
B) 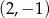 C)
C) 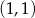 D)
D) 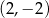
Proste o równaniach 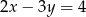 i
i 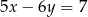 przecinają się w punkcie
przecinają się w punkcie 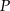 . Stąd wynika, że
. Stąd wynika, że
A) 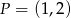 B)
B) 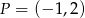 C)
C) 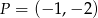 D)
D) 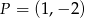
Proste o równaniach 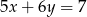 i
i 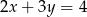 przecinają się w punkcie
przecinają się w punkcie 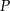 . Stąd wynika, że
. Stąd wynika, że
A) 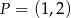 B)
B) 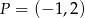 C)
C) 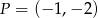 D)
D) 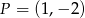
W kartezjańskim układzie współrzędnych 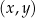 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami czworokąta 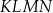 . Czworokąt
. Czworokąt 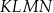 jest
jest
| A) | prostokątem, |
| B) | trapezem, który nie jest równoległobokiem |
| C) | równoległobokiem, który nie jest prostokątem, |
ponieważ
| 1) | czworokąt 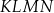 ma dwie osie symetrii. ma dwie osie symetrii. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | dwie z tych prostych są równoległe. |
W kartezjańskim układzie współrzędnych 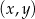 dane są proste
dane są proste 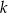 oraz
oraz 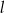 o równaniach
o równaniach
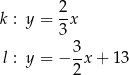
Proste 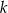 oraz
oraz 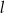
| A) są prostopadłe | B) nie są prostopadłe |
i przecinają się w punkcie 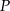 o współrzędnych
o współrzędnych
1. 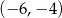 | 2. 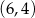 | 3. 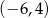 |
W kartezjańskim układzie współrzędnych 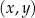 dane są proste
dane są proste 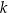 oraz
oraz 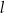 o równaniach
o równaniach
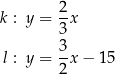
Proste 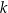 oraz
oraz 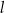
| A) są prostopadłe | B) nie są prostopadłe |
i przecinają się w punkcie 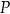 o współrzędnych
o współrzędnych
1. 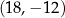 | 2. 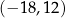 | 3. 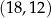 |
W kartezjańskim układzie współrzędnych 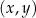 , danych jest 5 prostych o równaniach
, danych jest 5 prostych o równaniach
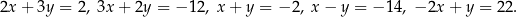
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych prostych są proste prostopadłe. | P | F |
| Wszystkie podane proste przecinają się w jednym punkcie. | P | F |
Proste 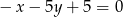 i
i 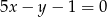 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 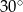 B)
B) 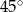 C)
C) 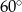 D)
D) 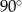
Proste 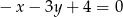 i
i 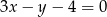 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 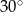 B)
B) 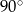 C)
C) 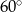 D)
D) 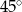
Proste 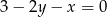 i
i 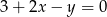 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze
A) 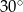 B)
B) 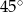 C)
C) 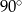 D)
D) 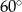
Dwa boki trójkąta 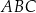 są zawarte w prostych
są zawarte w prostych 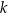 i
i 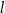 o równaniach
o równaniach
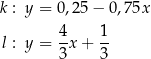
Trójkąt 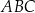
| A) jest prostokątny | B) nie jest prostokątny |
i jeden z jego wierzchołków może mieć współrzędne
1. 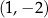 | 2. 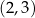 | 3.  |
Proste o równaniach 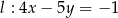 i
i 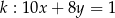
A) są równoległe B) są prostopadłe
C) przecinają się w punkcie 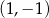 D) przecinają się w punkcie
D) przecinają się w punkcie 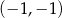
Proste o równaniach 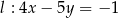 i
i 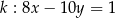
A) są równoległe B) są prostopadłe
C) przecinają się w punkcie 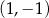 D) przecinają się w punkcie
D) przecinają się w punkcie 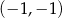
Proste o równaniach 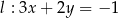 i
i 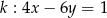
A) przecinają się w punkcie 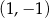 B) przecinają się w punkcie
B) przecinają się w punkcie 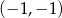
C) są równoległe D) są prostopadłe
W kartezjańskim układzie współrzędnych 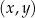 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 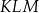 . Trójkąt
. Trójkąt 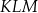 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 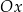 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 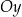 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
W kartezjańskim układzie współrzędnych 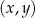 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 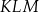 . Trójkąt
. Trójkąt 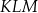 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 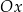 jest osią symetrii tego trójkąta. jest osią symetrii tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | jedna z tych prostych jest równoległa do osi 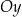 . . |
Proste o równaniach 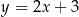 oraz
oraz 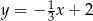
A) są równoległe i różne B) są prostopadłe
C) przecinają się pod kątem innym niż prosty D) pokrywają się
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 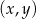 , dane są proste
, dane są proste 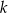 oraz
oraz 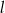 o równaniach
o równaniach
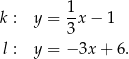
Proste  oraz
oraz 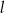
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 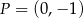 . D) pokrywają się.
. D) pokrywają się.
Równania 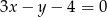 oraz
oraz 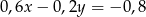 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 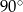
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 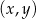 , dane są proste
, dane są proste 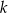 oraz
oraz 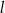 o równaniach
o równaniach
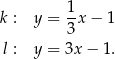
Proste 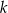 oraz
oraz 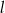
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 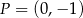 . D) pokrywają się.
. D) pokrywają się.
Równania 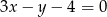 oraz
oraz 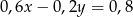 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż 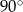
Równania 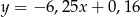 oraz
oraz 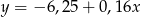 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 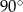 .
.
B) pokrywające się.
C) przecinające się pod kątem różnym od 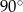 .
.
D) równoległe i różne.
Równania 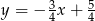 oraz
oraz 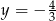 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 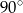 .
.
B) pokrywające się
C) przecinające się pod kątem różnym od 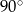 .
.
D) równoległe i różne.
Proste o równaniach 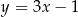 oraz
oraz 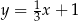
A) pokrywają się B) przecinają się pod kątem innym niż prosty
C) są prostopadłe D) są równoległe i różne
Proste o równaniach 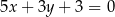 oraz
oraz 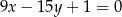
A) są równoległe i różne B) są prostopadłe
C) przecinają się pod kątem innym niż prosty D) pokrywają się
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 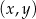 , dane są:
, dane są:
– prosta 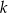 o równaniu
o równaniu 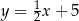
– prosta 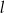 o równaniu
o równaniu 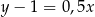 .
.
Proste 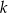 i
i 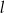
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 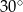 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 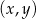 , dane są:
, dane są:
– prosta 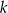 o równaniu
o równaniu 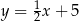
– prosta 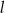 o równaniu
o równaniu 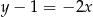 .
.
Proste 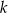 i
i 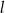
A) pokrywają się. B) nie mają punktów wspólnych.
C) są prostopadłe. D) przecinają się pod kątem 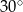 .
.
Równania 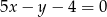 oraz
oraz 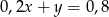 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) przecianją się pod kątem prostym
B) pokrywają się
C) są równoległe i nie pokrywają się
D) przecinają się pod innym kątem niż