Wykaż, że każda liczba pierwsza większa od 3 jest postaci 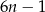 lub
lub 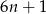 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej  .
.
/Szkoła średnia/Liczby/Liczby całkowite/Reszty
Udowodnij, że każda liczba całkowita 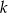 , która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby
, która przy dzieleniu przez 7 daje resztę 2, ma tę własność, że reszta z dzielenia liczby 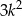 przez 7 jest równa 5.
przez 7 jest równa 5.
Reszta z dzielenia liczby całkowitej  przez 4 jest równa 3. Wyznacz resztę z dzielenia liczby
przez 4 jest równa 3. Wyznacz resztę z dzielenia liczby 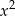 przez 4.
przez 4.
Reszta z dzielenia liczby całkowitej  przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby
przez 5 jest równa 4. Wyznacz resztę z dzielenia liczby 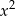 przez 5.
przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 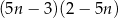 przy dzieleniu przez 25 daje resztę 19.
przy dzieleniu przez 25 daje resztę 19.
Liczba  z dzielenia przez 4 daje resztę 1. Liczba
z dzielenia przez 4 daje resztę 1. Liczba 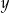 z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby
z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby 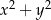 przez 8.
przez 8.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 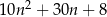 przy dzieleniu przez 5 daje resztę 3.
przy dzieleniu przez 5 daje resztę 3.
Wykaż, że dla każdej liczby całkowitej 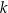 reszta z dzielenia liczby
reszta z dzielenia liczby 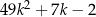 przez 7 jest równa 5.
przez 7 jest równa 5.
Wykaż, że dla każdej liczby całkowitej 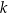 reszta z dzielenia liczby
reszta z dzielenia liczby 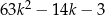 przez 7 jest równa 4.
przez 7 jest równa 4.
Wykaż, że jeżeli 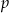 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 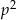 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Uzasadnij, że jeżeli liczba całkowita nie dzieli się przez 3, to jej kwadrat przy dzieleniu przez 3 daje resztę 1.
Uzasadnij, że jeżeli liczba całkowita jest nieparzysta, to jej kwadrat przy dzieleniu przez 8 daje resztę 1.
Wykaż, że dla każdej liczby naturalnej  reszta z dzielenia liczby
reszta z dzielenia liczby 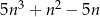 przez
przez 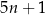 jest równa 1.
jest równa 1.
Wykaż, że suma kwadratów trzech liczb całkowitych, które przy dzieleniu przez 3 dają resztę 2 jest podzielna przez 3.
Wykaż, że jeżeli przy dzieleniu przez 7 jedna liczba daję resztę 3, a druga resztę 4, to iloczyn tych liczb daje przy dzieleniu przez 7 resztę 5.
Udowodnij, że jeżeli przy dzieleniu przez 5 liczba całkowita  daje resztę 2, a liczba całkowita
daje resztę 2, a liczba całkowita 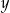 daje resztę 3, to iloczyn liczb
daje resztę 3, to iloczyn liczb  i
i 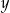 przy dzieleniu przez 5 daje resztę 1.
przy dzieleniu przez 5 daje resztę 1.
Wykaż, że jeżeli przy dzieleniu przez 5 jedna liczba daję resztę 2, a druga resztę 3, to iloczyn tych liczb daje przy dzieleniu przez 5 resztę 1.
Liczba naturalna  przy dzieleniu przez 5 daje resztę 3, liczba
przy dzieleniu przez 5 daje resztę 3, liczba 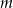 również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb
również przy dzieleniu przez 5 resztę 2. Udowodnij, że reszta z dzielenia iloczynu liczb 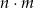 przez 5 daje resztę 1.
przez 5 daje resztę 1.
Liczby  i
i 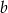 są nieparzyste i dają przy dzieleniu przez 4 różne reszty. Wykaż, że suma kwadratów tych liczb nie jest podzielna przez 4.
są nieparzyste i dają przy dzieleniu przez 4 różne reszty. Wykaż, że suma kwadratów tych liczb nie jest podzielna przez 4.
Reszta z dzielenia liczby  przez 3 jest równa 2. Reszta z dzielenia liczby
przez 3 jest równa 2. Reszta z dzielenia liczby 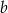 przez 3 jest równa 1. Wykaż, że różnica kwadratów liczb
przez 3 jest równa 1. Wykaż, że różnica kwadratów liczb  i
i 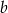 jest podzielna przez 3.
jest podzielna przez 3.
Reszta z dzielenia liczby  przez 4 jest równa 3. Reszta z dzielenia liczby
przez 4 jest równa 3. Reszta z dzielenia liczby 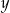 przez 4 jest równa 1. Wykaż, że różnica kwadratów liczb
przez 4 jest równa 1. Wykaż, że różnica kwadratów liczb  i
i 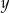 jest podzielna przez 4.
jest podzielna przez 4.
Wykaż, że reszta z dzielenia sumy kwadratów trzech kolejnych liczb naturalnych przez 3 jest równa 2.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych nieparzystych liczb naturalnych przez 16 jest równa 4.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 8 jest równa 6.
Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 4 jest równa 2.
Udowodnij, że reszta z dzielenia sumy kwadratów dwóch kolejnych liczb naturalnych niepodzielnych przez 3, przy dzieleniu przez 18 jest równa 5.
Wykaż, że dla każdej liczby naturalnej 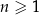 liczba
liczba 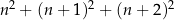 przy dzieleniu przez 3 daje resztę 2.
przy dzieleniu przez 3 daje resztę 2.
Udowodnij, że dla każdej liczby całkowitej  liczba
liczba 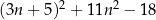 przy dzieleniu przez 5 daje resztę 2.
przy dzieleniu przez 5 daje resztę 2.
Uzasadnij, że jeżeli liczba całkowita  nie dzieli się przez 5, to
nie dzieli się przez 5, to 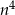 daje przy dzieleniu przez 5 resztę 1.
daje przy dzieleniu przez 5 resztę 1.

