Wykaż, że dla każdej liczby naturalnej 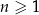 liczba
liczba 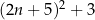 jest podzielna przez 4.
jest podzielna przez 4.
/Szkoła średnia/Liczby/Liczby całkowite/Podzielność/1 literka
Udowodnij, że jeżeli liczba całkowita  nie jest podzielna przez 3, to wyrażenie
nie jest podzielna przez 3, to wyrażenie 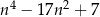 jest podzielne przez 9.
jest podzielne przez 9.
Wykaż, że jeżeli 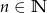 , to liczba postaci
, to liczba postaci 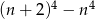 jest podzielna przez 16.
jest podzielna przez 16.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 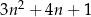 jest podzielna przez 4.
jest podzielna przez 4.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 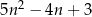 jest podzielna przez 4.
jest podzielna przez 4.
Pokazać, że dla każdej liczby naturalnej  liczba
liczba 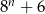 jest podzielna przez 7.
jest podzielna przez 7.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 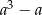 jest podzielne przez 3.
jest podzielne przez 3.
Wykaż, że dla każdej liczby naturalnej 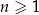 liczba
liczba 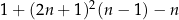 jest podzielna przez 24.
jest podzielna przez 24.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 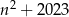 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 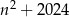 jest podzielna przez 3.
jest podzielna przez 3.
Wykaż, że jeżeli  jest liczbą nieparzystą to liczba
jest liczbą nieparzystą to liczba
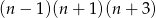
jest liczbą podzielną przez 48.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 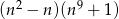 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 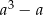 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że dla każdej liczby naturalnej 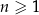 liczba
liczba 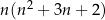 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 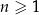 liczba
liczba 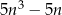 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 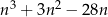 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 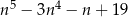 jest podzielne przez 16.
jest podzielne przez 16.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 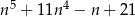 jest podzielne przez 16.
jest podzielne przez 16.
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 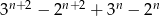 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Udowodnij, że dla każdej liczby naturalnej  , gdzie
, gdzie 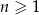 , liczba
, liczba 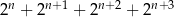 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że liczba 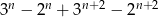 jest podzielna przez 10,
jest podzielna przez 10, 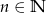 .
.
Wykaż, że jeśli 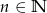 , to liczba
, to liczba 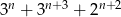 jest podzielna przez 4.
jest podzielna przez 4.
Uzasadnij, że dla każdej liczby całkowitej 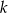 liczba
liczba 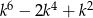 jest podzielna przez 36.
jest podzielna przez 36.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 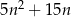 jest podzielna przez 10.
jest podzielna przez 10.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 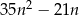 jest podzielna przez 14.
jest podzielna przez 14.
Wykaż, że dla każdej liczby naturalnej 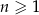 liczba
liczba 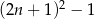 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że dla każdej liczby naturalnej 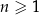 liczba
liczba 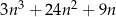 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 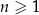 liczba
liczba 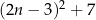 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że dla każdej liczby naturalnej 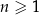 liczba
liczba 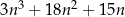 jest podzielna przez 6.
jest podzielna przez 6.
Uzasadnij, że jeżeli  jest liczbą naturalną to liczba
jest liczbą naturalną to liczba 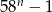 dzieli się przez 19.
dzieli się przez 19.
Liczba  jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba
jest liczbą całkowitą parzystą, która nie dzieli się przez 4. Wykaż, że liczba 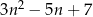 nie jest podzielna przez 4.
nie jest podzielna przez 4.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 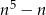 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 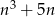 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 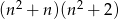 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 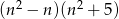 jest podzielna przez 6.
jest podzielna przez 6.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 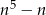 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 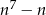 jest podzielna przez 7.
jest podzielna przez 7.

