W zbiorze 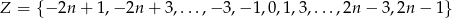 , gdzie
, gdzie 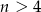 jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi
jest liczbą naturalną, zmieniono znaki na przeciwne trzem losowo wybranym liczbom. Wiadomo, że prawdopodobieństwo tego, że suma wszystkich liczb w zbiorze nie uległa zmianie wynosi 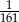 . Wyznacz
. Wyznacz  .
.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Różne
Ze zbioru liczb 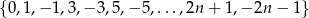 , gdzie
, gdzie  jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech
jest ustaloną liczbą naturalną, większą od 4, losujemy jednocześnie trzy liczby. Niech 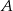 oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że
oznacza zdarzenie: suma wylosowanych liczb nie ulegnie zmianie, jeżeli w wylosowanych liczbach zmienimy znaki na przeciwne. Wiedząc, że 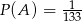 , oblicz
, oblicz  .
.
W grze liczbowej Express Lotek losowanych jest pięć spośród liczb 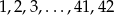 . Gracz zawarł jeden zakład na najbliższe losowanie (czyli wytypował w kolekturze Totalizatora Sportowego pięć liczb spośród czterdziestu dwóch). Oblicz ile razy prawdopodobieństwo trafienia ’trójki’ (czyli wytypowania dokładnie 3 liczb spośród tych, które będą wylosowane) jest większe niż prawdopodobieństwo trafienia
. Gracz zawarł jeden zakład na najbliższe losowanie (czyli wytypował w kolekturze Totalizatora Sportowego pięć liczb spośród czterdziestu dwóch). Oblicz ile razy prawdopodobieństwo trafienia ’trójki’ (czyli wytypowania dokładnie 3 liczb spośród tych, które będą wylosowane) jest większe niż prawdopodobieństwo trafienia
- piątki;
- czwórki.
Ze zbioru 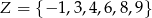 losujemy bez zwracania liczby
losujemy bez zwracania liczby  i
i 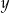 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń: 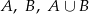 jeśli:
jeśli:
A – suma wylosowanych liczb jest nieparzysta;
B – wylosowane liczby spełniają warunek: 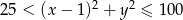 .
.
Ze zbioru 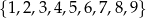 losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
Zamek szyfrowy składa się z 5 tarcz. Na każdej z tarcz znajduje się 6 cyfr. Zamek otwiera kombinacja cyfr podana w odpowiedniej kolejności. (istotne są cyfry na tarczach oraz kolejność ustawiania tarcz). Jakie jest prawdopodobieństwo otworzenia zamka przy losowym ustawieniu tarcz?
Ze zbioru wszystkich trójwyrazowych ciągów o wyrazach ze zbioru 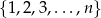 losujemy jeden ciąg.
losujemy jeden ciąg.
- Oblicz prawdopodobieństwo wylosowania ciągu rosnącego lub malejącego.
- Dla jakiej liczby naturalnej
 prawdopodobieństwo to jest równe 0,125?
prawdopodobieństwo to jest równe 0,125?
Ze zbioru liczb 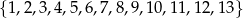 losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
Każdy z trojga chłopców pomyślał sobie liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że żadne dwie z tych osób nie pomyślały tej samej liczby? Wynik podaj w postaci ułamka nieskracalnego.
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba trzycyfrowa ma cyfrę setek mniejszą od cyfry dziesiątek, a cyfrę jedności równą cyfrze setek.
Z pudełka, w którym jest 15 kul ponumerowanych kolejnymi liczbami od 1 do 15, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 16.
Z pudełka, w którym jest 13 kul ponumerowanych kolejnymi liczbami od 1 do 13, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 14.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 30. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest o 85 większa od drugiej. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru siedmiu liczb naturalnych 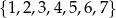 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
Ze zbioru ośmiu liczb naturalnych 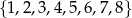 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
Ze zbioru liczb 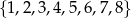 wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
Spośród liczb 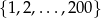 wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa
wybieramy losowo bez zwracania dwie liczby. Oblicz prawdopodobieństwa 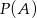 i
i 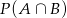 , gdzie
, gdzie 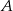 i
i 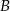 są następującymi zdarzeniami:
są następującymi zdarzeniami: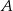 – druga z wylosowanych liczb jest mniejsza od 2;
– druga z wylosowanych liczb jest mniejsza od 2;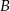 – różnica wylosowanych liczb jest podzielna przez 3.
– różnica wylosowanych liczb jest podzielna przez 3.
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy kolejno trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 304.
Ze zbioru 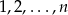 losujemy kolejno bez zwracania 2 liczby
losujemy kolejno bez zwracania 2 liczby 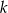 i
i 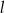 . Dla jakich wartości
. Dla jakich wartości  prawdopodobieństwo tego, że
prawdopodobieństwo tego, że 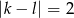 jest większe od
jest większe od 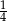 ?
?
Ze zbioru liczb 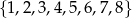 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 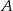 , polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
, polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
Ze zbioru liczb 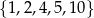 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 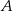 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą.
Ze zbioru liczb 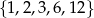 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 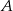 polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
polegającego na tym, że iloraz pierwszej wylosowanej liczby przez drugą wylosowaną liczbę jest liczbą całkowitą parzystą.
Ze zbioru ośmioelementowego 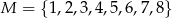 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 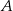 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 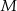 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 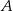 .
.
Ze zbioru dziewięcioelementowego 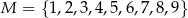 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 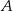 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 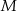 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 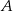 .
.

