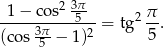Wykaż, że dla dowolnego kąta  prawdziwa jest tożsamość
prawdziwa jest tożsamość 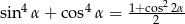 .
.
/Szkoła średnia/Funkcje/Trygonometryczna/Tożsamości
- Sprawdź, czy równość
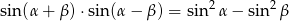
jest tożsamością trygonometryczną.
- Udowodnij, że jeżeli
 i
i 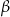 są dwoma kątami trójkąta i
są dwoma kątami trójkąta i 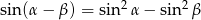 , to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
, to trójkąt ten jest trójkątem prostokątnym lub równoramiennym.
Uzasadnij, że jeżeli 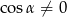 to prawdą jest, że
to prawdą jest, że 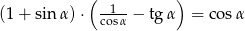 .
.
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to
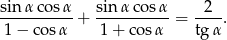
Wykaż, że dla każdego kąta ostrego  prawdziwy jest wzór
prawdziwy jest wzór 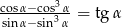 .
.
Wykaż, że 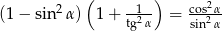 .
.
Wykaż tożsamość 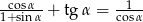 .
.
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
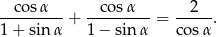
Sprawdź czy równość jest tożsamością. Podaj odpowiednie założenia.
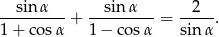
Wykaż, że 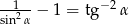 .
.
Uzasadnij, że dana równość 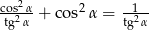 jest prawdziwa.
jest prawdziwa.
Wykaż, że dla dowolnego kąta  takiego, że
takiego, że 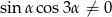 zachodzi tożsamość
zachodzi tożsamość
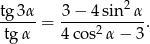
Wykaż, że 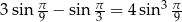 .
.
Wykaż, że wyrażenie 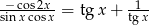 nie jest tożsamością.
nie jest tożsamością.
Udowodnij, że jeżeli 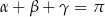 , to
, to
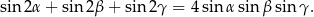
Udowodnij, że jeżeli 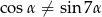 i
i 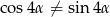 to
to
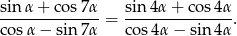
Udowodnij, że jeżeli 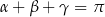 , to
, to
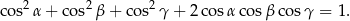
Sprawdź tożsamość: 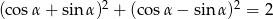 .
.
Uzasadnij, że równość 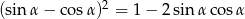 jest tożsamością trygonometryczną.
jest tożsamością trygonometryczną.
Uzasadnij, że równość 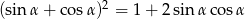 jest tożsamością trygonometryczną.
jest tożsamością trygonometryczną.
Wykaż, że
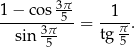
Wykaż, że jeżeli 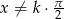 dla
dla 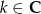 to prawdziwa jest tożsamość
to prawdziwa jest tożsamość
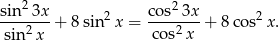
Wykaż, że 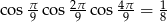 .
.
Wykaż, że

Wykaż, że
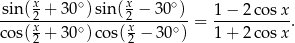
Wykaż, że
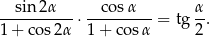
Wyznacz dziedzinę tej tożsamości.
Wykaż, że
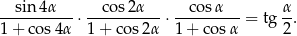
Wyznacz dziedzinę tej tożsamości.
Wykaż, że 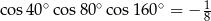 .
.
Wykaż, że
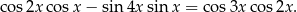
Wykaż, że jeżeli 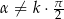 , gdzie
, gdzie 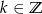 , to
, to
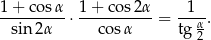
Sprawdź, czy prawdziwa jest następująca tożsamość 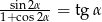 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Sprawdź, czy prawdziwa jest następująca tożsamość 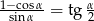 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Sprawdź, czy prawdziwa jest tożsamość 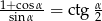 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Wykaż, że