Dany jest wykres funkcji 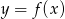 określonej dla
określonej dla 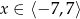 .
.
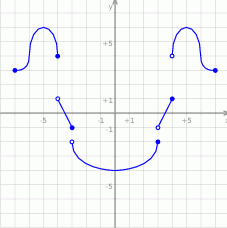
Odczytaj z wykresu:
- rozwiązania równania
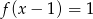 ;
; - miejsca zerowe funkcji
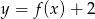 ;
; - maksymalne przedziały monotoniczności funkcji
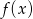 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest wykres funkcji 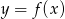 określonej dla
określonej dla 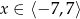 .
.

Odczytaj z wykresu:
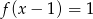 ;
; 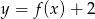 ;
; 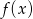 .
.Dany jest wykres funkcji 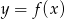 określonej dla
określonej dla 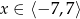 .
.
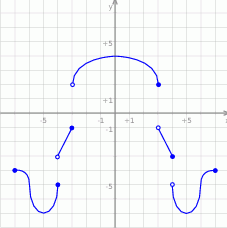
Odczytaj z wykresu:
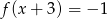 ;
; 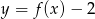 ;
; 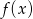 .
.Na rysunku przedstawiono wykres funkcji 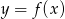 .
.
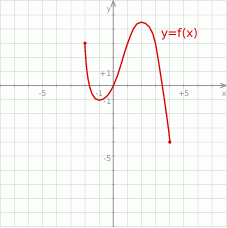
Naszkicuj wykres funkcji: 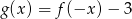 . Określ dziedzinę oraz miejsca zerowe funkcji
. Określ dziedzinę oraz miejsca zerowe funkcji 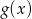 .
.
Na rysunku przedstawiony jest wykres funkcji 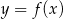 .
.
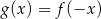 .
. 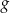 jest rosnąca.
jest rosnąca.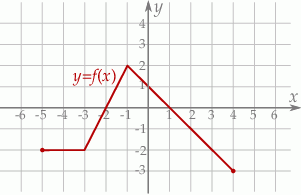
Na rysunku przedstawiony jest wykres funkcji 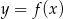 .
.
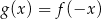 .
. 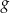 jest rosnąca.
jest rosnąca.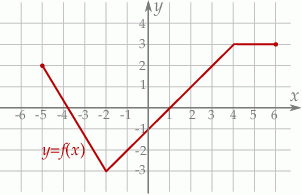
Poniżej znajduje się fragment wykresu funkcji 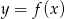 .
.
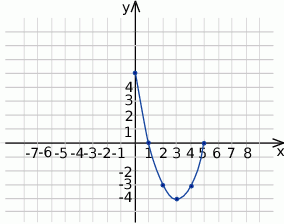
Dorysuj brakującą część wykresu wiedząc, że dziedziną funkcji 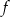 jest przedział
jest przedział 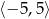 , a wykres jest symetryczny względem osi
, a wykres jest symetryczny względem osi 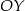 . Następnie na podstawie wykresu funkcji
. Następnie na podstawie wykresu funkcji 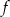 :
:
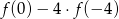 ;
; 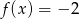 .
.W kartezjańskim układzie współrzędnych 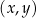 narysowano wykres funkcji
narysowano wykres funkcji 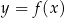 (zobacz rysunek).
(zobacz rysunek).
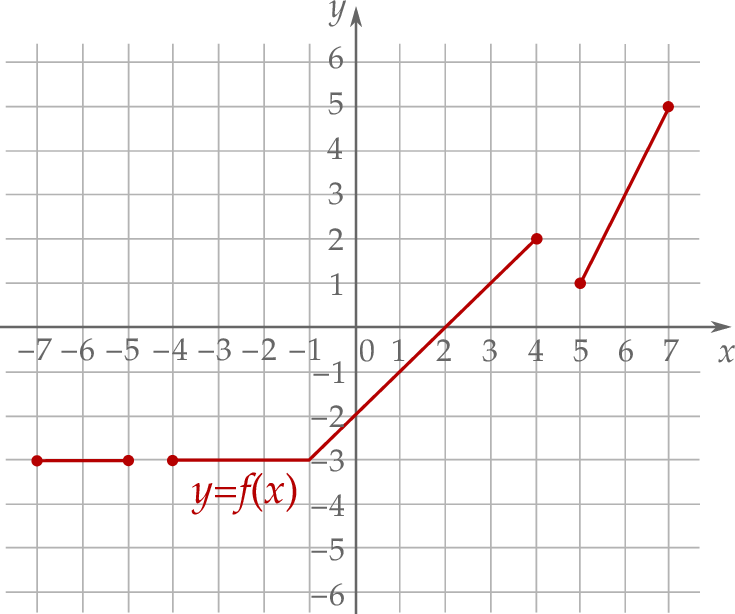
Wyznacz zbiór wszystkich argumentów, dla których funkcja 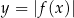 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Funkcja 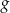 określona wzorem
określona wzorem 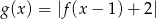 , gdzie
, gdzie 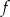 jest funkcją, której wykres przedstawiono obok. Podaj zbiór rozwiązań nierówności
jest funkcją, której wykres przedstawiono obok. Podaj zbiór rozwiązań nierówności 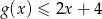 .
.
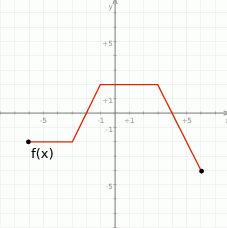
Na rysunku przedstawiony jest wykres pewnej funkcji 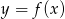 .
.
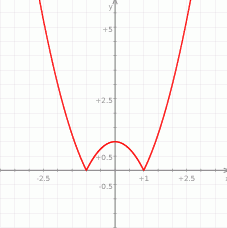
Naszkicuj na oddzielnych rysunkach wykresy funkcji: 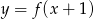 i
i 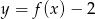 .
.
W kartezjańskim układzie współrzędnych 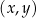 narysowano wykres funkcji
narysowano wykres funkcji 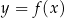 (zobacz rysunek).
(zobacz rysunek).
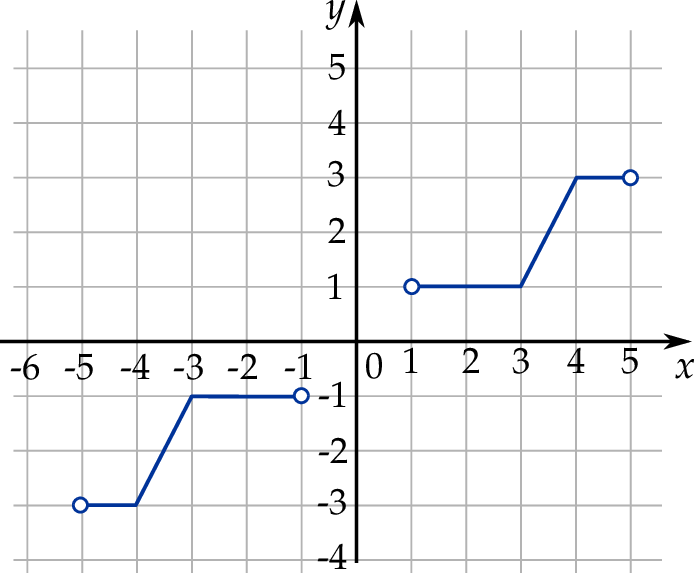
Zapisz poniżej zbiór wszystkich rozwiązań nierówności 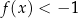 .
.
W kartezjańskim układzie współrzędnych 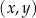 narysowano wykres funkcji
narysowano wykres funkcji 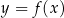 (zobacz rysunek).
(zobacz rysunek).
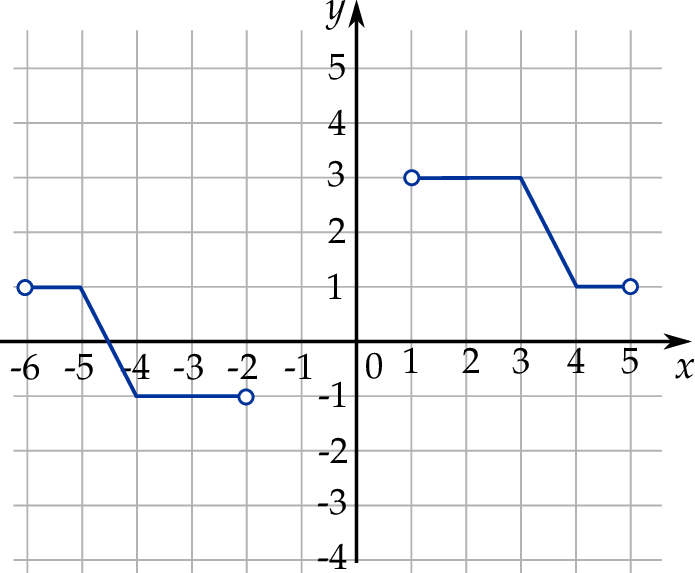
Zapisz poniżej zbiór wszystkich rozwiązań nierówności 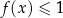 .
.
W kartezjańskim układzie współrzędnych 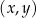 narysowano wykres funkcji
narysowano wykres funkcji 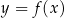 (zobacz rysunek).
(zobacz rysunek).
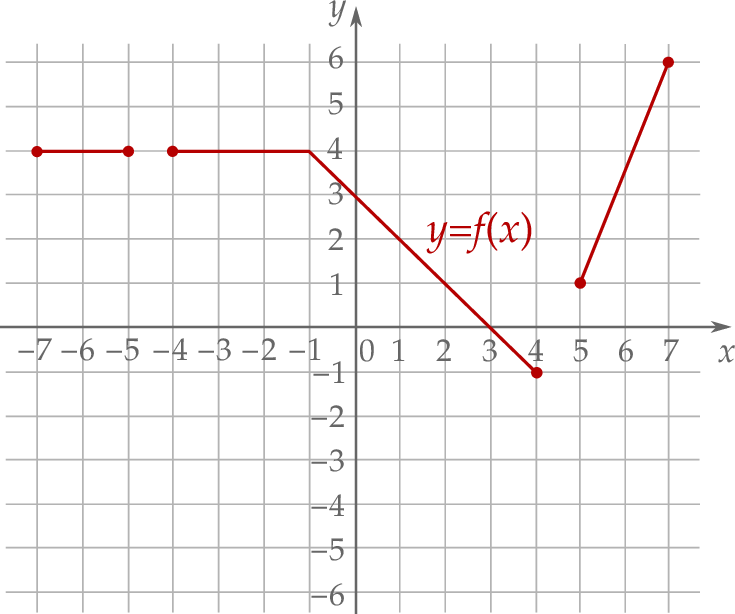
Wyznacz zbiór wszystkich argumentów, dla których funkcja 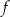 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
W kartezjańskim układzie współrzędnych 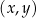 narysowano wykres funkcji
narysowano wykres funkcji 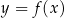 (zobacz rysunek).
(zobacz rysunek).
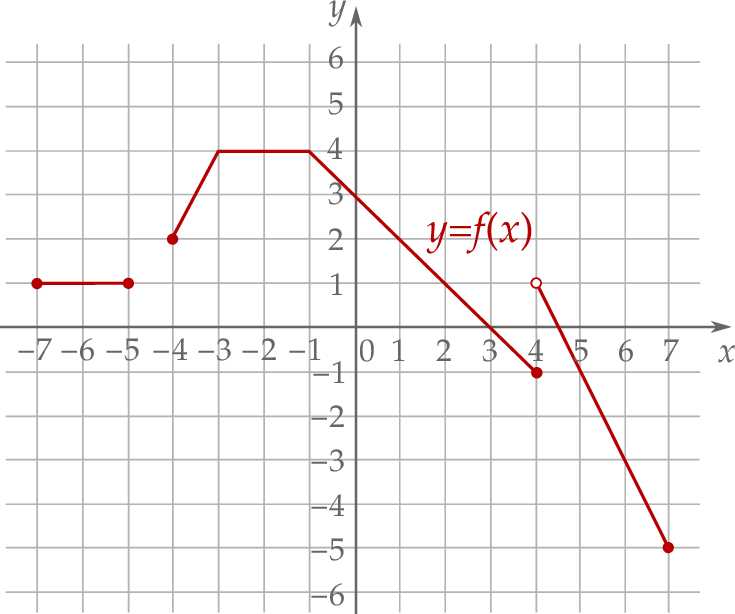
Wyznacz zbiór rozwiązań nierówności 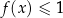 .
.
Wykres funkcji 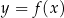 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 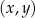 na rysunku poniżej.
na rysunku poniżej.
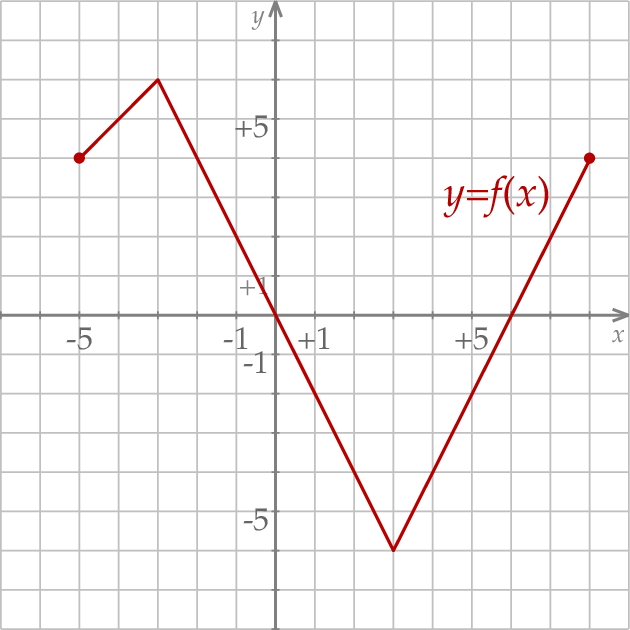
Wyznacz zbiór rozwiązań nierówności 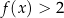 .
.
Na rysunku, w kartezjańskim układzie współrzędnych 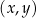 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 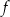 . Każdy z punktów przecięcia wykresu funkcji
. Każdy z punktów przecięcia wykresu funkcji 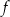 z prostą o równaniu
z prostą o równaniu 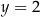 ma obie współrzędne całkowite.
ma obie współrzędne całkowite.
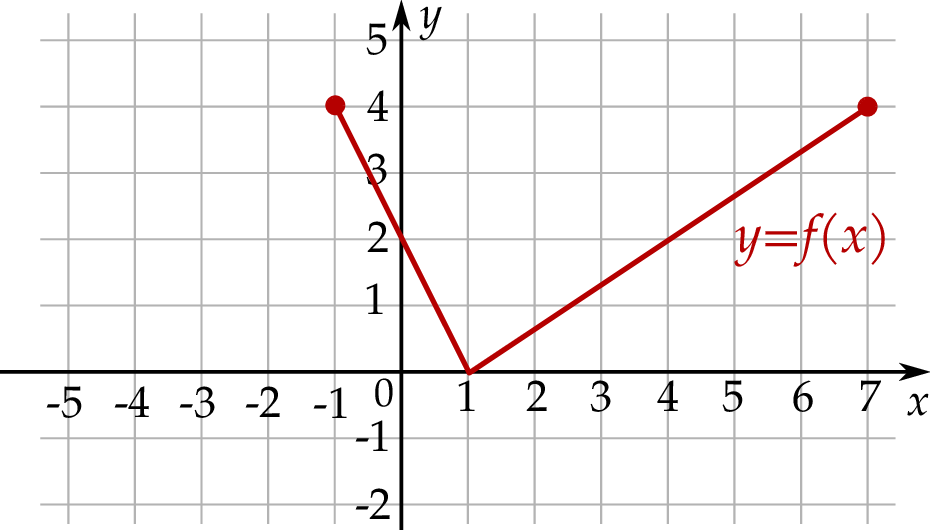
Wyznacz zbiór rozwiązań nierówności 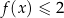 .
.
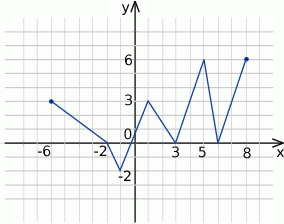
Na podstawie podanego wykresu funkcji 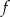
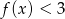 ;
; ![g(x) = [f(x )]2](https://img.zadania.info/zad/3151872/HzadT3x.gif) przecina prostą
przecina prostą 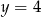 .
.Na podstawie podanego wykresu funkcji 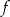
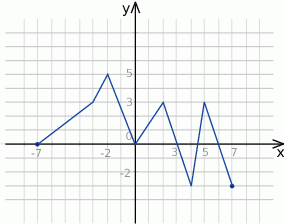
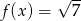 .
. ![g(x) = [f (x )]2](https://img.zadania.info/zad/6954447/HzadT3x.gif) przecina prostą
przecina prostą 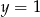 .
.W kartezjańskim układzie współrzędnych 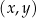 narysowano wykres funkcji
narysowano wykres funkcji 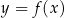 (zobacz rysunek).
(zobacz rysunek).
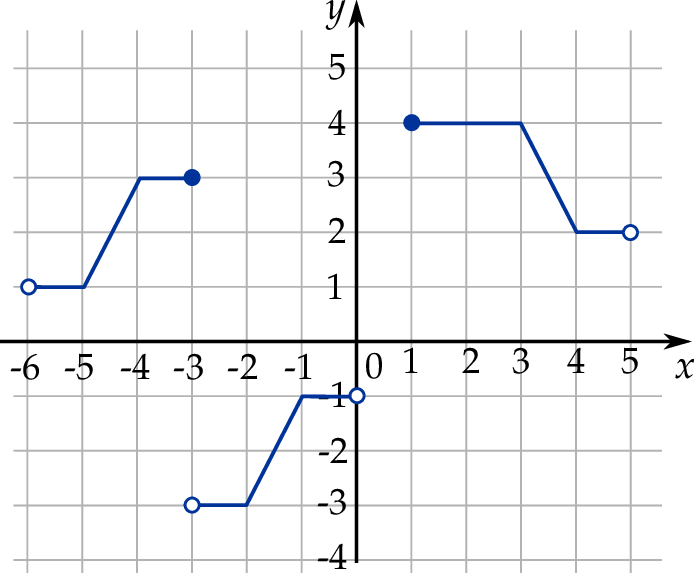
Wyznacz zbiór wszystkich rozwiązań nierówności 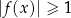 .
.
Funkcja 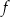 jest określona następująco
jest określona następująco
![( |{ x+ 4 dla x ∈ [− 8,0] f(x) = 4 dla x ∈ (0,4] |( − 2x+ 12 dla x ∈ (4,6)](https://img.zadania.info/zad/3798099/HzadT1x.png)
Wykres funkcji 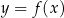 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 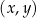 na rysunku poniżej.
na rysunku poniżej.
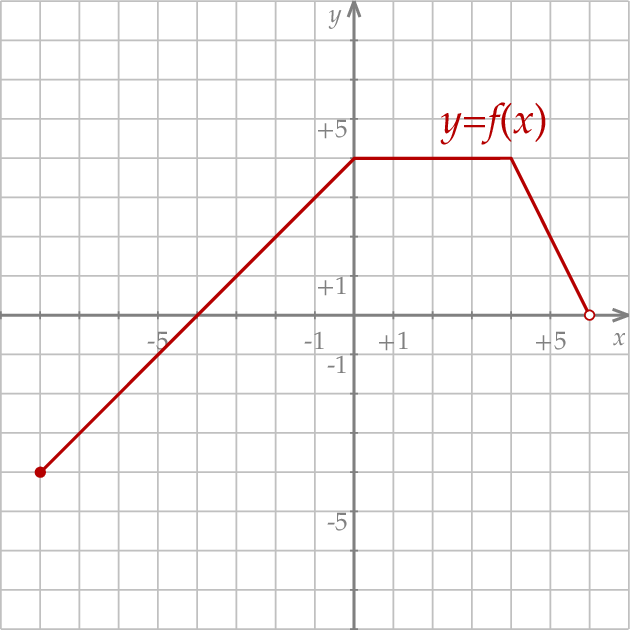
Wyznacz dziedzinę funkcji 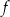 .
.
Wyznacz zbiór wartości funkcji 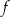 .
.
Wyznacz zbiór wszystkich argumentów, dla których funkcja 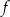 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne.
Wyznacz zbiór wszystkich rozwiązań równania 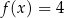 .
.
Na rysunku przedstawiono wykres funkcji 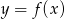 .
.
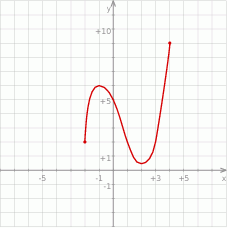
Naszkicuj wykres funkcji: 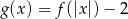 . Określ dziedzinę oraz miejsca zerowe funkcji
. Określ dziedzinę oraz miejsca zerowe funkcji 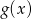 .
.
Na rysunku przedstawiono wykres funkcji 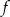 .
.
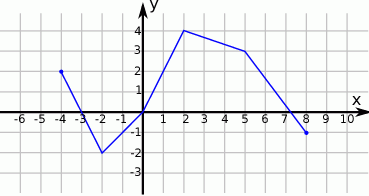
Odczytaj z wykresu i zapisz:
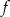 ,
, 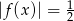 .
.Poniżej znajduje się fragment wykresu funkcji 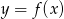 . Wiedząc, że dziedziną tej funkcji jest przedział
. Wiedząc, że dziedziną tej funkcji jest przedział 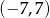 i wykres funkcji jest symetryczny względem punktu
i wykres funkcji jest symetryczny względem punktu 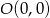 , dorysuj brakującą część wykresu. Następnie na podstawie wykresu funkcji
, dorysuj brakującą część wykresu. Następnie na podstawie wykresu funkcji 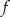 podaj:
podaj:
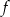
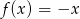 .
.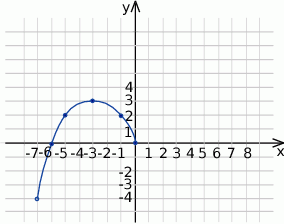
Na rysunku przedstawiono wykres funkcji 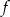 .
.
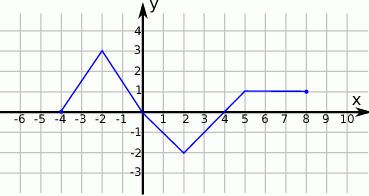
Odczytaj z wykresu i zapisz:
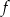 ,
, 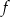 jest malejąca.
jest malejąca.Na rysunku przedstawiono wykres funkcji 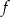 .
.
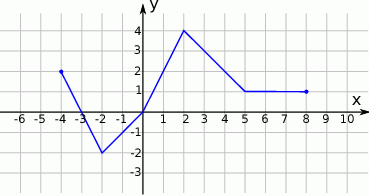
Odczytaj z wykresu i zapisz:
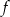 ,
, 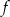 jest rosnąca.
jest rosnąca.Na rysunku przedstawiony jest wykres funkcji 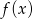 określonej dla
określonej dla 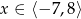 .
.
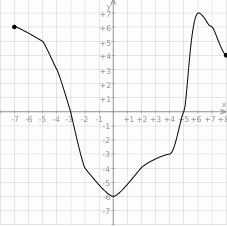
Odczytaj z wykresu i zapisz:
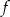 ,
, 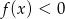 .
.Odczytaj z wykresu
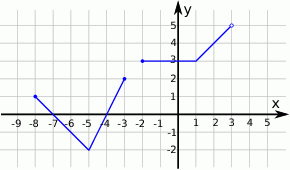
Na rysunku przedstawiony jest wykres funkcji 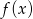 określonej dla
określonej dla 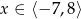 .
.
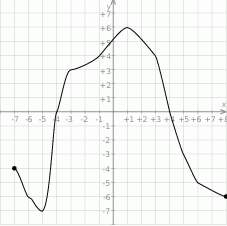
Odczytaj z wykresu i zapisz:
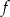 ,
, 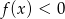 .
.Na rysunku poniżej przedstawiony jest wykres funkcji 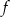 , określonej w przedziale
, określonej w przedziale 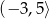 .
.
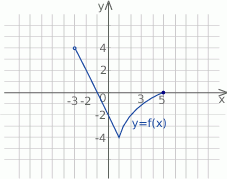
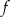 .
. 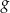 , opisanej wzorem
, opisanej wzorem 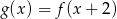 .
. 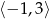 , dla których wartości funkcji
, dla których wartości funkcji 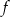 są większe niż wartości funkcji
są większe niż wartości funkcji 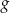 .
.Na rysunku przedstawiony jest wykres funkcji 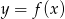 . Dla jakich argumentów funkcja
. Dla jakich argumentów funkcja 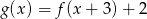 jest rosnąca?
jest rosnąca?
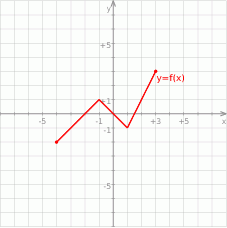
Na rysunku jest przedstawiony wykres funkcji 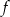 .
.
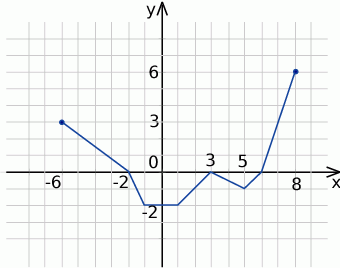
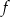 .
. 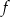 .
. 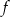 dla argumentu
dla argumentu 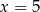 .
. 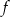 .
. 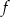 jest rosnąca.
jest rosnąca. 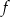 przyjmuje wartości ujemne.
przyjmuje wartości ujemne. Na rysunku, w kartezjańskim układzie współrzędnych 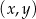 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 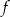 określonej dla każdego
określonej dla każdego ![x ∈ (− 6,5]](https://img.zadania.info/zad/5539913/HzadT2x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
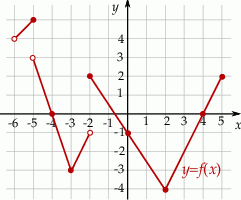
Wyznacz zbiór wartości funkcji 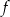 .
.
Na rysunku przedstawiono pewną funkcję 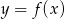 określoną w przedziale
określoną w przedziale  .
.
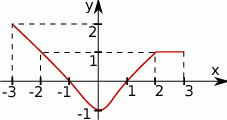
Określ na podstawie wykresu tej funkcji:
Z wykresu funkcji 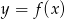 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
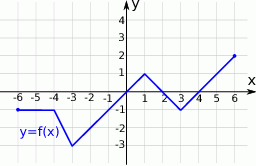
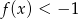 .
.Poniżej przedstawiony jest wykres funkcji 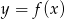 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
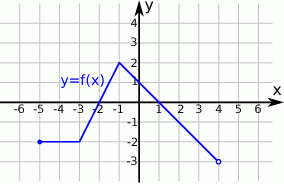
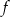 ;
; 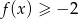 .
.Z wykresu funkcji 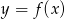 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
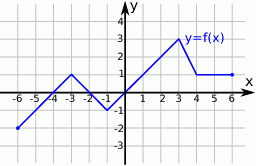
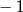 ;
; 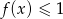 .
.Z wykresu funkcji 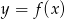 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
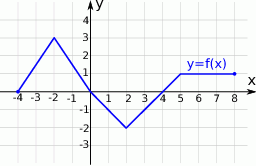
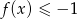 .
.Poniżej przedstawiony jest wykres funkcji 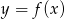 . Na podstawie tego wykresu podaj:
. Na podstawie tego wykresu podaj:
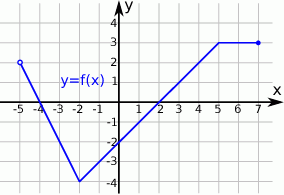
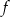 ;
; 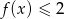 .
.Z wykresu funkcji 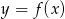 przedstawionego na rysunku odczytaj:
przedstawionego na rysunku odczytaj:
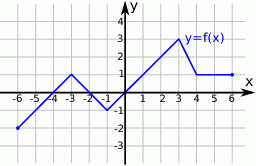
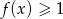 .
.